例说常数数列法巧求两类数列的通项公式
闫西宝
(江苏省徐州市第七中学,221000)
例说常数数列法巧求两类数列的通项公式
闫西宝
(江苏省徐州市第七中学,221000)
在数列问题中,求通项公式最常见的两种类型是:已知首项a1,且满足an+1=an+f(n)或者an+1=anf(n),其所用的方法是累加法和累乘法.在教学实践中,笔者发现解决这两类问题,和可用同一种简洁的方法,即构造常数数列法,下面举例说明.
一、an+1=an+f(n)型
对于此类型的数列,可设g(n+1)-g(n)=f(n),则有an+1-g(n+1)=an-g(n),故数列{an-g(n)}是常数数列,所以an-g(n)=a1-g(1),即an=g(n)+a1-g(1),g(n)可通过观察法或待定系数法求得.
例1已知数列{an}满足,a1=1,an+1=an+2n+1,求数列{an}的通项公式.
解由an+1=an+2n+1,f(n)=2n+1,不妨设g(n)=an2+bn.
由g(n+1)-g(n)=2n+1,得
a(n+1)2+b(n+1)-(an2+bn)
=2n+1
对任意n∈N*恒成立,所以有
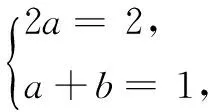
所以an+1-(n+1)2=an-n2,即数列{an-n2}是常数数列,
因此an-n2=a1-1,
又a1=1,所以an=n2.
例2已知数列{an}满足a1=1,an+1=an+3n,求数列{an}的通项公式.
解因为an+1=an+3n,
所以g(n+1)-g(n)=3n.
不妨设g(n)=a·3n.
由g(n+1)-g(n)=3n,得
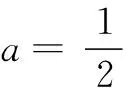
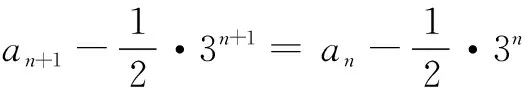










二、an+1=anf(n)型
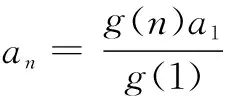
g(n)可通过观察法或待定系数法求得.
例4在数列{an}中,已知a1=1,an+1=2n·an,求数列{an}的通项公式.
解因为an+1=2n·an,所以

不妨设g(n)=2an2+bn,

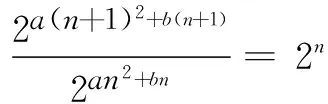
即a(n+1)2+b(n+1)-(an2+bn)=n
对任意n∈N*恒成立,所以有
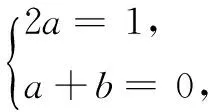
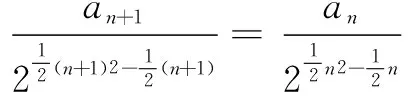


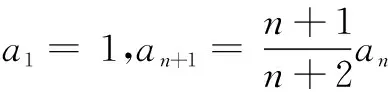
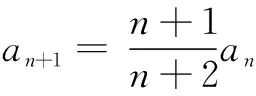
(n+2)an+1=(n+1)an,
即{(n+1)an}是常数数列.
于是(n+1)an=2a1,由a1=1,得
例6已知数列{an}满足,a1=2,(n+2)an+1=nan,求数列{an}的通项公式.
分析因为已知(n+2)an+1=nan中,n+2和n不是相邻两项,所以要将n+2和n变成相邻两项,两边同乘n+1即可.
解由(n+2)an+1=nan,两边同乘n+1,得
(n+2)(n+1)an+1=(n+1)nan.
于是{(n+1)nan}是常数数列,有
(n+1)nan=2a1,

累加法和累乘法,大部分学生都能理解并掌握,但在解题中,由于书写复杂和细节等问题,容易出错.常数数列法书写简洁,不易出错,可作为上面两种方法的补充.

