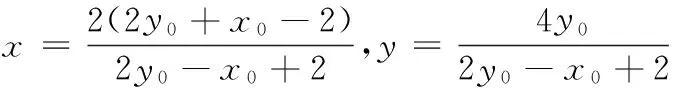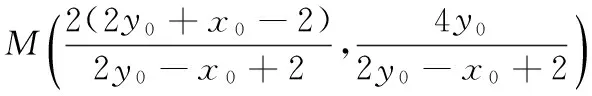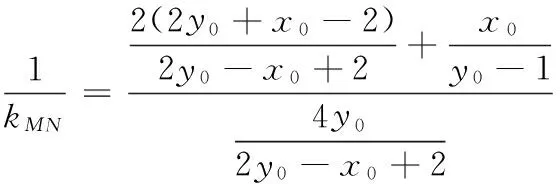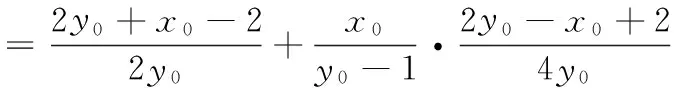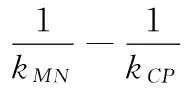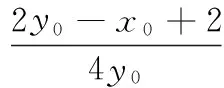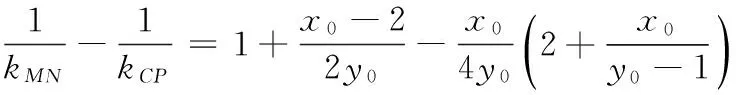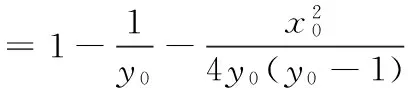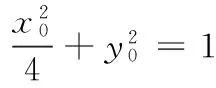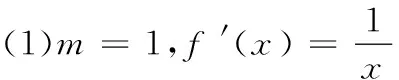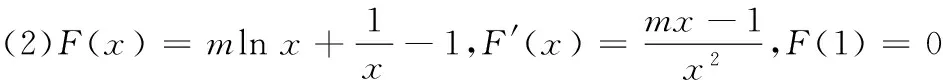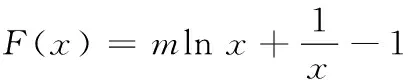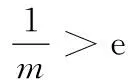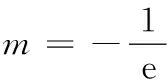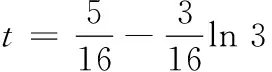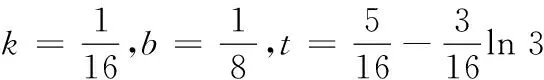高二数学测试



高二数学测试

一、填空题(本大题共14小题，每小题5分，共70分)

1.抛物线y2=8x的焦点F的坐标为______.

3.某校高一有550名学生,高二有700名学生,高三有750名学生,学校为了解学生的课外阅读情况,决定按年级分层抽样,抽取100名学生,则高二年级应抽取______名学生.

4.从1,2,3中任选两个数字构成一个两位数,则该两位数是偶数的概率为______.

5.已知双曲线C的一条渐近线方程为y=x,则该双曲线的离心率为______.

7.如图所示的伪代码,则输出的S的值为______.

For n From 1 to 11 Step 2

S←S+n

End For

Print S

第7题图

9.设函数f(x)=x2+x-aln x,则a<3是函数f(x)在[1,+∞)上单调递增的______条件. (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)

10.(理科学生做)四名高二学生报名参加数学、物理、化学三门学科竞赛,要求每名学生都参加且只参加1门学科竞赛,则3门学科都有学生参赛的种数有______种.

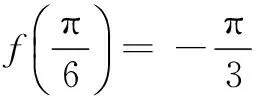
11.(理科学生做)在(x2-3x+2)4的展开式中,x2项的系数为______.(用数字作答)

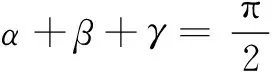
13.若一元二次不等式mx2+(2-m)x-2>0恰有3个整数解,则实数m的取值范围是______.

二、解答题(本大题共6小题,共计90分.解答应写出必要的文字说明、证明过程或演算步骤)

(1)求甲只通过一所大学考试的概率;

(2)设三名学生中同时通过两所大学考试的人数为X,求X的概率分布与数学期望.

(文科学生做)设命题p:函数f(x)=x3+ax2+ax是R上的单调递增函数,命题q:|a-1|≤m(m>0).

(1)当a=1时,判断命题p的真假,并说明理由;

(2)若q是p的充分不必要条件,求实数m的取值范围.

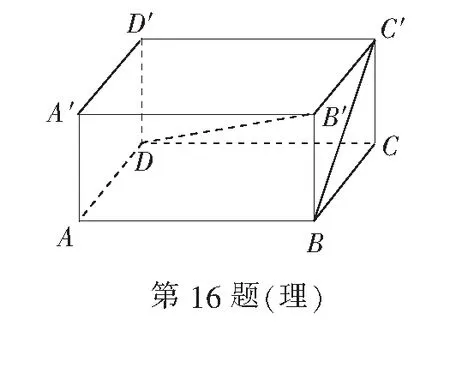
16.(本小题满分14分) (理科学生做)在长方体ABCD-A′B′C′D′中,AB=4,BC=CC′=2.求

(1)直线B′D与BC′所成角的大小;

(2)二面角A-B′D-C的余弦值.

(1)求f(x)在(0,π)上的单调增区间;

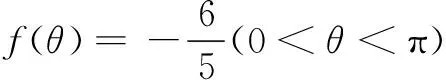
(1)求a2,a3的值;

(2)猜想an与3的大小关系,并用数学归纳法证明.

(2)猜想f(x)的正负,并证明.

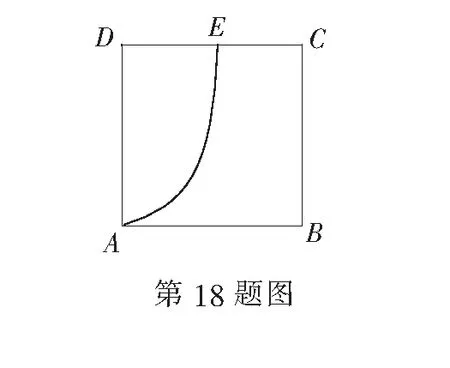
18.(本小题满分16分)如图,已知四边形ABCD是一块边长为2千米的正方形地皮,其中曲边三角形ADE是一个小池塘,点E在边CD上且DE=1千米.假设曲边AE可用以A为顶点,AD为对称轴的抛物线拟合,现绿化部门拟过曲边AE上一点P作切线，交边AB于点M,交边CD于点N,在四边形MBCN内栽种花草.

(1)建立适当的坐标系,用点P的横坐标t表示花草的面积S(t),并写出定义域;

(2)求S(t)的最大值.

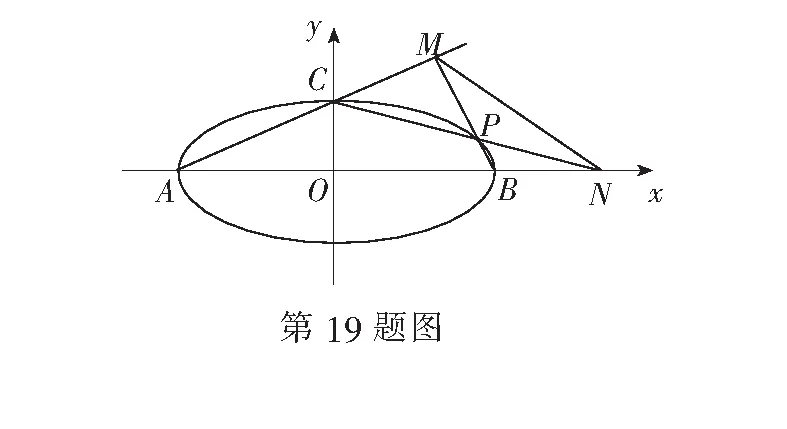
(1)求椭圆E的方程;

(2)直线AC与PB交于点M,直线CP交x轴于点N.

① 当点M在以AB为直径的圆上时,求点P的横坐标;

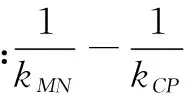
(1)当m=1时,求y=f(x)在x=1处的切线方程;

(2)设F(x)=f(x)-2g(x),若函数F(x)在区间[1,e]上的最小值为-1,求实数m的值;

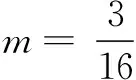
参考答案

一、填空题

6.7；7.36;8.真；9.充分不必要；

12.tan αtan β+tan βtan γ+tan γtan α=1;

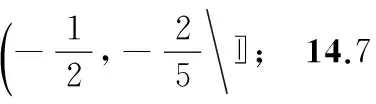
二、解答题

15.(理)(1)记甲通过A大学而不通过B大学考试为事件E，甲通过B大学而不通过A大学考试为事件F，则

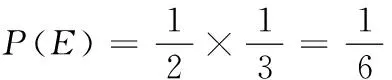
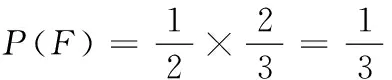
所以甲只通过一所大学考试的概率

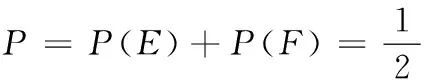
(2)每名学生同时通过两所大学考试的概率

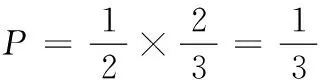
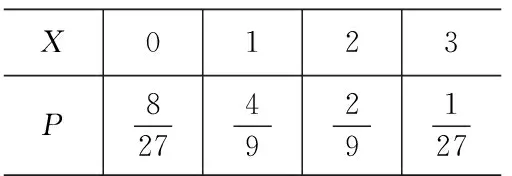
X0123P8274929127

(文)(1)因f(x)是R上的单调递增函数，所以

f ′(x)=3x2+2ax+a≥0,

所以Δ=4a2-12a≤0,解得0≤a≤3,

所以当a=1时，命题p为真命题.

(2)由|a-1|≤m(m>0)，解得1-m≤a≤1+m.

因q是p的充分不必要条件，所以q⟹p,

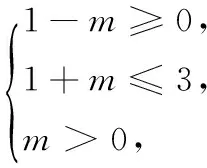
又当m=1时，p≠q，所以实数m的取值范围是(0,1].

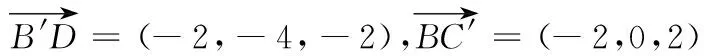
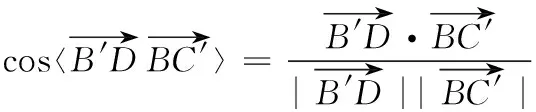
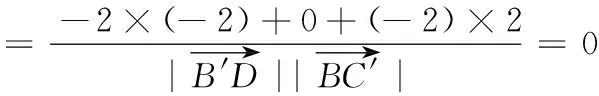
设平面AB′D的法向量n1=(x1,y1,z1),则

所以x1=0.

令y1=1,则z1=-2,

所以面AB′D的一个法向量n1=(0,1,-2),

同理面B′DC的一个法向量n2=(1,0,-1).

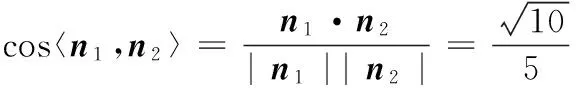
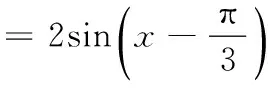
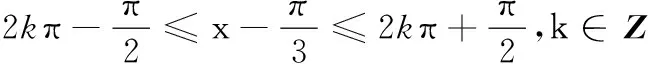
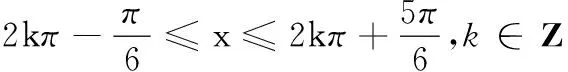
(2)由(1)可得

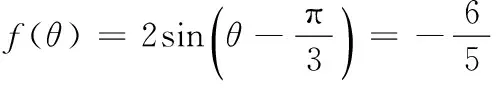
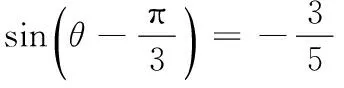
又∵0<θ<π,

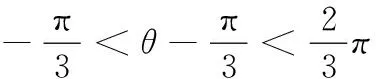
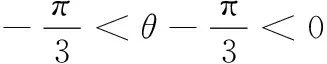
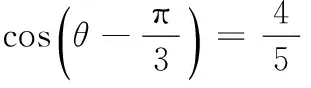
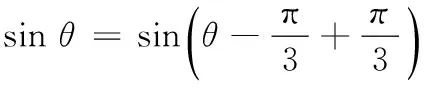
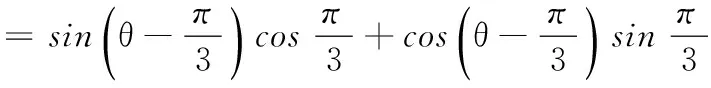
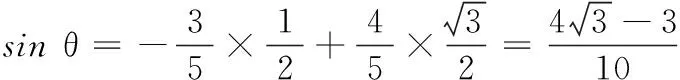
17.(理)(1)由题意，得

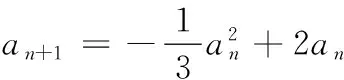
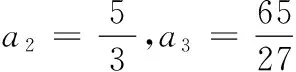
(2)猜想an<3.

证明：①当n=1时，a1=1<3,结论成立，

②假设n=k时，结论成立，即ak<3,

则n=k+1时，

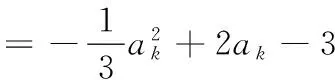
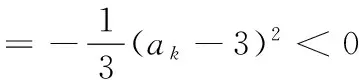
所以ak+1<3.

根据①②，猜想成立.

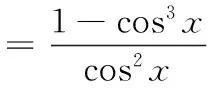
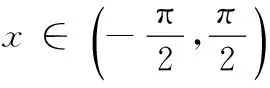
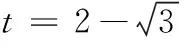
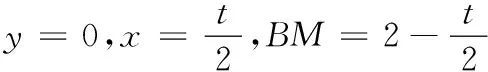
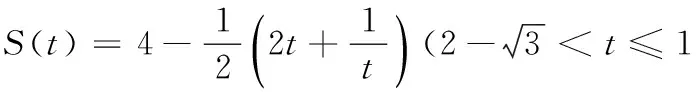
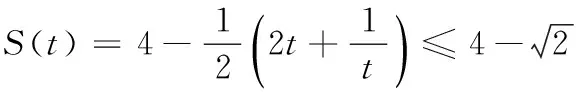
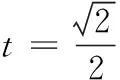
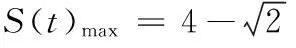
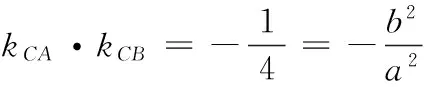
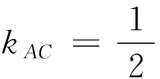
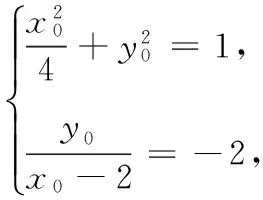
消去y0,得17x20-64x0+60=0,

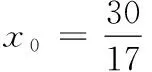
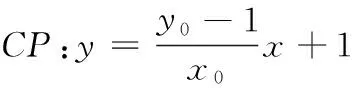
联立直线AC，BP的方程，有