高三数学综合测试
高三数学综合测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.f(x)=3sin x,x∈[0,2π]的单调减区间为______.
2.若复数z=1+ai(i是虚数单位)的模不大于2,则实数a的取值范围是______.
3.若方程ln x+2x-10=0的解为x0,则大于x0的最小整数是______.


6.下列说法中,正确的有______.(写出所有正确命题的序号)
① 若f ′(x0)=0,则f(x0)为f(x)的极值点;
② 在闭区间[a,b]上,极大值中最大的就是最大值;
③若f(x)的极大值为f(x1),f(x)的极小值为f(x2),则f(x1)>f(x2);
④有的函数有可能有两个最小值;
⑤已知函数f(x)=ex,对于f(x)定义域内的任意一个x1都存在唯一个值x2,使f(x1)f(x2)=1成立.
7.设向量a,b的夹角为θ,a=(2,1),a+3b=(5,4),则sin θ=______.

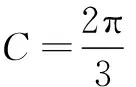

13..设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是______.
14.已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f ′(x)≤f(x).若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,则M的最小值为______.
二、解答题:(本大题共6小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分14分)已知



(1)求θ;
(2) 求满足f(x)=1,x∈[-π,π]的x的集合.
16.(本小题满分14分)已知命题p:指数函数f(x)=(2a-6)x在R上单调递减,命题q:关于x的方程x2-3ax+2a2+1=0的两个实根均大于3.若“p或q”为真,“p且q”为假,求实数a的取值范围.

(1)求角C的大小;
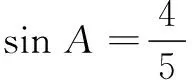
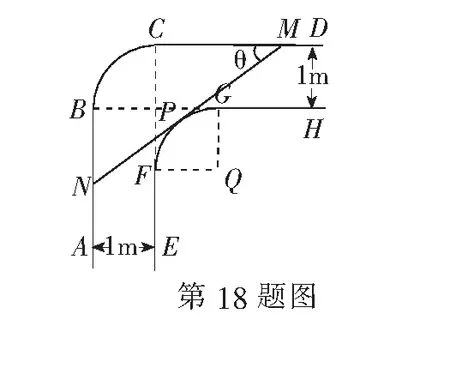
18.(本小题满分16分)一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1 m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1 m.
(1)若水平放置的木棒MN的两个端点M,N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P,设∠CMN=θ(rad),试用θ表示木棒MN的长度f(θ);
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
20.(本小题满分16分)设f(x)是定义在区间(1,+∞)上的函数,其导函数为f ′(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f ′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
① 求证:函数f(x)具有性质P(b);② 求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x1,x2∈(1,+∞),x1
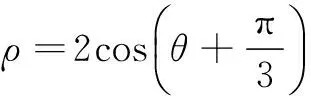
(1)写出曲线C的参数方程,直线l的普通方程;
(2)过曲线C上任一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
23. (附加题,本小题满分10分)抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示(0 纪念币ABC概率12aa 将这三枚纪念币同时抛掷一次,设ξ表示出现正面向上的纪念币的个数. (1)求ξ的分布列及数学期望; (2)在概率P(ξ=i)(i=0,1,2,3)中,若P(ξ=1)的值最大,求a的最大值. 24. (附加题,本小题满分10分)如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数). (2)试问:直线EF与直线EA能否垂直?请说明理由. 一、填空题 二、解答题 17.(1)由题意,得 所以∆ABC的面积 ①若S在线段TG上,则TS=QT-QS. ②若S在线段GT的延长线上,则 TS=QS-QT. 在Rt∆STM中, 19. (1)函数f(x)的定义域为(0,+∞), 由题意可得f(1)=2,f ′(1)=e, 故a=1,b=2. h′(x)=e-x(1-x). 综上,当x>0时,g(x)>h(x),即f(x)>1. ∴函数f(x)具有性质P(b). ②设φ(x)=x2-bx+1,则f ′(x)与φ(x)同号. 当b∈[-2,2]时,φ(x)=x2-bx+1>0恒成立,∴f(x)在(1,+∞)上单调递增; 当b∈(-∞,-2)时,φ(x)=x2-bx+1>0恒成立,∴f(x)在(1,+∞)上单调递增; (2)依据题意,g′(x)=h(x)(x-1)2, ∴g(x)在(1,+∞)单调递增,且有 α+β=x1+x2,α-β=(2m-1)(x1-x2). α-x1=(m-1)x1+(1-m)x2, β-x2=(1-m)x1+(m-1)x2, ∴(α-x1)(β-x2)=-(m-1)2(x1-x2)2<0. ∴α 若α f(α) ∴g(α)-g(β)>g(x1)-g(x2),不合题意. ∴x1<α<β 0=|g(α)-g(β)| α-x1=(x1-x2),β-x1=-m(x1-x2). 同理有x1<β<α 综上,0 22.(1)曲线C的参数方程为 直线l的普通方程为2x+y-6=0. (2)曲线C上任意一点P(2cos θ,3sin θ)到l的距离 23.(1)ξ的分布列 ξ0123P12(1-a)212(1-a2)12(2a-a2)a22 取y=1,则n=(2,1,2). 化简,得3λ2-2λ+3=0, 因为Δ=4-36<0,所以该方程无解,所以假设不成立,即直线EF不可能与直线EA垂直.


参考答案


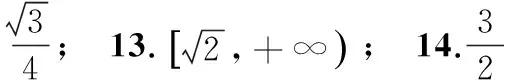
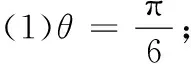


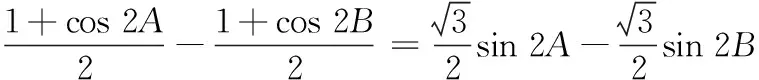
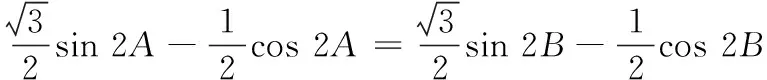


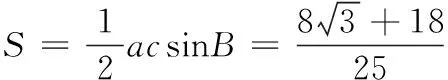






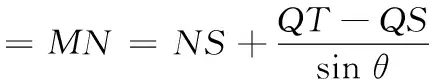
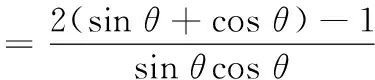




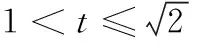



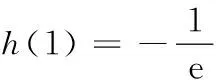







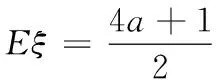



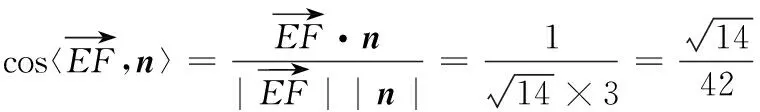
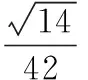

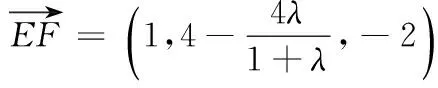
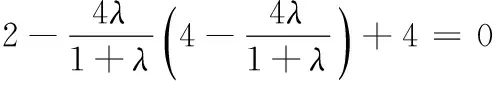
——庆祝中国共产党成立一百周年贵金属纪念币展

