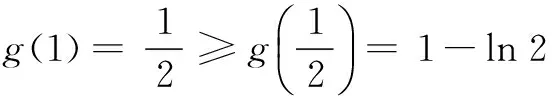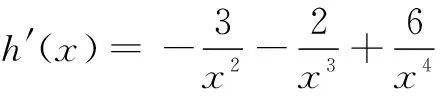一道高考试题的三种解法
张业山 苏凡文
(山东省宁阳一中,271400)
一道高考试题的三种解法
张业山苏凡文
(山东省宁阳一中,271400)
题目(2016年山东高考题)已知

(1)讨论f(x)的单调性;
解(1)解题过程结论如下:
当a≤0时,f(x)的增区间为(0,1),减区间为(1,+∞);
当a=2时,f(x)增区间为(0,+∞);
(2)方法1(作差法)

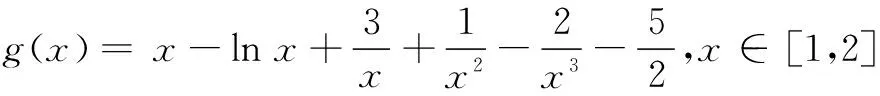



令h(x)=x3+6x2+6x-24,显然h(x)在[1,2]上为增函数.
因为h(1)=-11<0,h(2)=20>0,所以存在x1∈(1,2),使h(x1)=0.
(A)c (C)b 练习2设函数f(x)在R上存在导函数f ′(x),∀x∈R,有f(-x)+f(x)=x2,在(0,+∞)上,f(x) (A)[-2,2] (B) [2,+∞) (C)[0,+∞) 练习3定义在(0,2)内的函数f(x),f ′(x)是它的导函数,且恒有f(x) 练习提示:1.设函数 f(x)=-1; 3. 设函数 f(x)=-1. 所以当x∈(1,x1)时,h(x)<0,g″(x)<0,g′(x)为减函数; 当x∈(x1,2)时,h(x)>0,g″(x)>0,g′(x)为增函数. 所以x∈(1,x2)时,g′(x)>0,g(x)为增函数; x∈(x2,2)时,g′(x)<0,g(x)为减函数. 所以g(x)min=min{g(1),g(2)}. 方法2(比较法) 所以g(x)max=max{g(1),g(2)}. >2.8-0.35-2.25=0.2>0, 方法3(放缩法) 设g(x)=x-ln x-1,x∈[1,2],则 所以g(x)在[1,2]上为增函数,g(x)≥g(1)=0,所以x-ln x-1≥0,只需证明 所以h(x)min=min{h(1),h(2)}. 综上,g(x)≥0,当且仅当x=1时取等号;h(x)≥0,当且仅当x=2时取等号.