对一类特殊的椭圆焦点三角形的研究
2016-11-10 10:16:14孙延
高中数学教与学 2016年19期
孙 延
(四川省富顺县第二中学,643200)
对一类特殊的椭圆焦点三角形的研究
孙延
(四川省富顺县第二中学,643200)

证明如图1,以F1F2为直径作圆,记该圆与椭圆的交点为P,则该圆的半径c与椭圆的短半轴b满足c≥b.
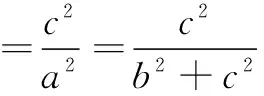
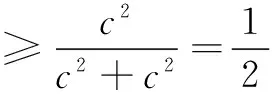

∵椭圆的离心率e∈(0,1),
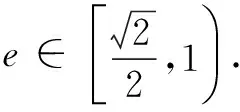

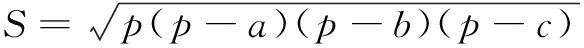
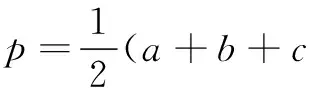
两边同除以面积平方,得



∴S′=


得证.
三角形有4个.
性质1在直焦点三角形F1PF2中,
|PF1||PF2|=2b2.
证明在∆F1PF2中,由余弦定理,可得
|F1F2|2=|PF1|2+|PF2|2
=(|PF1|+|PF2|)2
-2|PF1||PF2|.
∴(2c)2=(2a)2-2|PF1||PF2|,
化简得|PF1||PF2|=2b2.
性质2直焦点三角形面积S=b2.
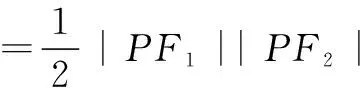
=b2.
性质3设顶点P的坐标为(xP,yp),则有


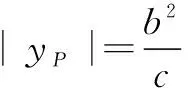
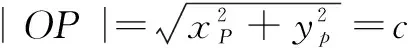
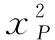
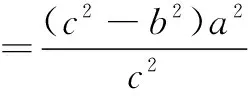

证明在∆F1PF2中,不妨设∠PF1F2=α,则
2csin α=|PF1|,
2ccos α=|PF2|,
2c(sin α+cos α)
=|PF1|+|PF2|=2a,

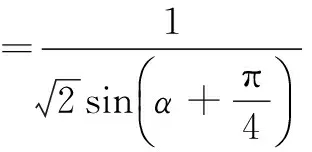
现利用以上结论解决引例中的问题:


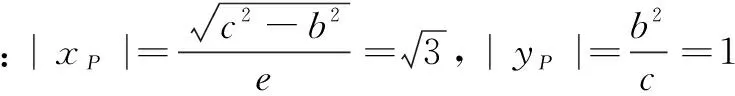
设∠OF1P=α,由性质4可知离心率

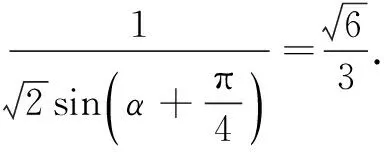
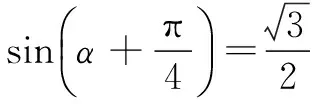
猜你喜欢
园林科技(2021年1期)2022-01-19 03:13:58
小资CHIC!ELEGANCE(2022年1期)2022-01-11 07:59:50
四川劳动保障(2021年1期)2021-01-28 21:51:04
四川劳动保障(2021年5期)2021-01-27 13:21:26
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
四川农业科技(2019年4期)2019-05-27 12:20:50
南方周末(2018-03-08)2018-03-08 08:34:56
科学中国人(2017年22期)2018-01-02 05:05:06

