抓不变量巧解题
2018-01-24 21:38◎刘乐
小学生学习指导(高年级) 2018年3期
◎刘 乐
在解决长方体与正方体的实际问题时,经常会出现一些改变形状的问题。这类问题如果我们能抓住题目中的不变量去解决,就能迅速获解。
例1:把2个长12厘米、宽10厘米、高6厘米的小长方体铁块熔铸成一个大的长方体铁块(损耗不计),大长方体铁块长是16厘米,高是6厘米,它的宽是多少厘米?
【分析与解】
这道题是把2个小长方体铁块熔成一个大长方体铁块,在熔铸的过程中,前后的体积不变,它是一个不变量。因此,可以先求出原来的体积,再用2个小正方体的总体积除以大长方体铁块的长和高,就可以求出它的宽。
解:(1)熔成大长方体的体积:

(2)大长方体的宽:
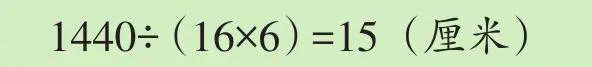
答:它的宽是15厘米。
例2:将一个长为8厘米的长方体的长减少3厘米,变成了一个正方体,长方体的体积减少了105立方厘米,原来这个长方体的体积是多少立方厘米?
【分析与解】
解题的关键是找出题目中不变的量,根据题意可知这个长方体的长减少了3厘米,变成了正方体,这里虽然形状变了,但侧面积没有变,它是一个不变量。因此,可根据减少的105立方厘米求出侧面积,再根据侧面积乘以长就可以求出原来长方体的体积。
解:(1)原来长方体的侧面积:

(2)原来长方体的体积:
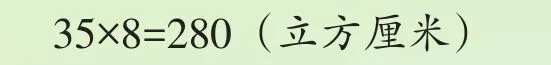
答:原来这个长方体的体积是280立方厘米。
猜你喜欢
小学生学习指导(低年级)(2021年9期)2021-10-14
小学生学习指导(低年级)(2021年3期)2021-07-21
作文中学版(2020年9期)2020-11-24
作文·初中版(2020年9期)2020-10-12
中学生数理化·高三版(2019年1期)2019-07-03
小学生学习指导(低年级)(2018年12期)2018-12-29
小学生学习指导(低年级)(2018年9期)2018-09-26
中学生数理化·高一版(2016年4期)2016-11-19
读写算·高年级(2009年8期)2009-08-12
中学生数理化·高一版(2008年4期)2008-11-15

