练好常态下设计的基本功:教材解读*

湖南省常德市芷兰实验学校　陈金红　黄克勤湖南省常德市安乡县芦林铺中学　郭作华

练好常态下设计的基本功:教材解读*

笔者近五年来一直担任湖南文理学院承担项目"湖南省初中数学骨干教师脱产研修"授课教师和"网络远程培训"坊主,前不久本届几个学员到我办公室当面求问:如何做好常态下教案设计(非加工后的教案设计)?现任教的2014级初中生,正好使用的是新湘教版八年级上册教材[1](体例发生了很大的变化、第一次使用!),笔者的基本经验自认为必由之路是搞好"教材解读"!为了真实地传递笔者的一些基本粗糙的做法,结合当时下节准备上的内容第46-48页第2章第一节"三角形(3)"做了一个现场设计,具体环节分享如下.

一、教材解读

1.文本呈现

第46页动脑筋图2-12(1),折叠三角形纸板,可以把它的三个角拼成一个角.

解读:操作的本质:把三角形的三个内角"没有缝隙"地聚合在三角形的一边上,从操作中让学生发现其和为一个平角即180°!

发问:你不妨试试,能一次性做到吗?操作里面包含的数学原理是学生暂且还没有学到的知识和技法!增加了很多的变数和疑惑,也不是本节课能解决的!既不符合学生的认知规律,也不是本节的教学导向!即揭示:折叠有巧合性!

如何站在文本的肩膀上改进、完善?结合其本质原理"弱化"要求,即先把其中的两个内角用"数学化"的方法聚合在三角形的一边上,再证明第三个内角也能"溜到"剩余的一个"缝隙位置"!从而自然得到"三角形三个内角的和等于180°"!

对于前者,可调动学生的基本经验:"经过直线外一点有且只有一条直线平行于已知直线"和"平行线的性质",具体为:在边BC上任取一点D,过点D作DE∥AB、DF∥AC,依次得到∠EDC=∠B、∠FDB=∠C、∠A(=∠BFD)=∠FDE圯∠A+∠B+∠C=∠BDC=180°.显然,这么处理符合学生的认知特征和学习心理,既可望又可及!见图1、图2.

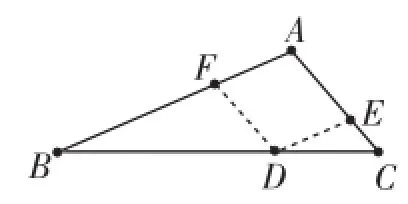
图1

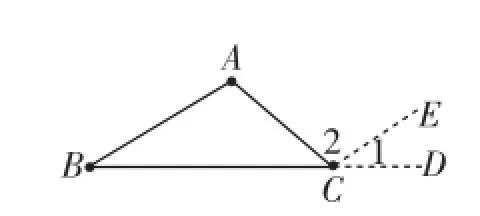
图2

2.文本呈现

第46页动脑筋图2-12(2),可以将∠A、∠B剪下并移至顶点C处拼接成一个角.

解读:操作的本质:把三角形的三个内角"没有缝隙"地聚合在顶点C上,从操作中让学生发现其和为一个平角即180°!

发问:你不妨试试,由于工具和操作的"误差"积累,最后一个角的"在右边的边"是否一定和内角∠ACB的"在左边的边"在同一直线上?揭示:论证的必须性!同时揭示在证明之前,必须把BC边反向延长!也只是把两个内角"请到"顶点C处!和上面第一图弱化后的方法一模一样!既有方法上的"一脉相承",更有方法上的同性化归和基本经验积累的伏笔和铺垫,不可小视教材编写的意图和解读!

3.文本呈现

第46页"由此受到启发:".

解读:在操作方法的基本经验的积累之下,发现基本经验的重要性,也告诉同学们站在经验的高度下是我们数学学习的规定动作和由此及彼产生自选动作的源泉!其次,提醒数学方法的它寻,古云"欲穷千里目"只好"更上一层楼",这正是新课标积极倡导的主题!

4.文本呈现

第47页议一议:一个三角形的三个内角中,最多有几个直角?几个钝角?

解读:教材目的是为了揭示三角形的第二种分类法(按角).

发问:三角形中的内角就只有直角和钝角吗?应该还有锐角,故这个议题少了一个分支!建议改为"议一议:一个三角形的三个内角中,最多有几个锐角?几个直角?几个钝角?"

其次,如何把此议题与三角形分类有机地结合起来?方法很重要,否则上下文过渡不自然、逻辑不清晰!即必须既注意逻辑链的培养,又必须注意思维链的生成!

做法:一个角很自由,可以是?(锐角、直角、钝角),但把它放在三角形"环境"中,可就受约束了,受控于? (三个内角的和为180度!)从而自然提出了议题:"议一议:一个三角形的三个内角中,最多有几个锐角?几个直角?几个钝角?"顺理成章地按角分类了!

5.文本呈现

第47页"外角"定义,第48页探究:在图2-15中,外角∠ACD和与它不相邻的内角∠A、∠B之间有什么大小关系?

解读:教材是直接呈现外角定义和直接证明外角和内角关系这个性质的.

发问:为何不能充分利用动脑筋图,站在已有经验和一手资料的肩膀上更深入地研究和启迪学生,为学生研读课本做有效阅读的示范呢?

做法:镜头回放,再次审视第46页剪拼法图2-12(2),你会发现什么?(特殊的现象)

如:发现∠ACD是把分散的内角∠A、∠B集中在内角∠ACB的顶点处,发现∠ACD与内角∠ACB在位置上共顶点、共一边,另一边互为反向延长线,发现∠ACD与内角∠ACB在数量上互补,发现∠ACD与两个内角∠A、∠B的和相等等,大量的信息资源"咕噜咕噜"地流动起来了!于是基于特殊的事情"特事特办"的原则,采取如下措施.

①基于∠ACD的位置,与内角∠ACB"两共一反"起名为三角形的一个外角,于是定义出:与三角形的一个内角共顶点、共一边,另一边互为反向延长线,这样的角就叫三角形的一个外角;②基于∠ACD的数量特征,与内角∠ACB互补.结合首例证明得出"三角形的一个外角等于和它不相邻的两个内角的和",于是一气呵成地、自然过渡地、深入而浅显地、直观轻松地解决了后两个知识点!再在理解一个的基础上,展开三角形外角数量及其关系的探寻、位置变式下的数量关系巩固训练等!

聪明的自然会发出另一个声音:镜头回放,审视第46页折叠图2-12(1),变化一下,你又会发现什么特殊的现象?既然可让"上面"的顶点翻折到一边上,我也可以翻折到三角形内部,亦可以翻折到三角形的外部,这正是我们常见的经典题(见图3、4、5)的自然来头!

6.文本呈现

关于练习题和习题:第46页练习1、2、3和第49页A组第4、5题和B组第7、8题.

解读:教材第46页练习1两个小题基本意图是运用三角形内角和及方程组的方法,建议增加一小问:按角分类它会是什么类型的三角形(下同)?其次允许思路与方法的多样性!练习2基本意图同上及三角形角平分线定义的运用,练习3基本意图纯粹是三角形外角性质的运用.揭示从"课本练习"定"课堂达标(基本要求)".

再看第49页A组第4、5题和B组第7、8题,除了本课时的要求,还结合了本阶段的基本要求.特别是B组第7题有一般的规律,若让点P自由运动到三角形内部(本题)、BC边上、三角形外部,则别有一番风采!将可极大地激发学生的学习兴趣和思维的活力,更引领了变化的思想方法和分类的动态特征与科学探究的一般操作方式!还有B组第8题一道经典的五角星题,思维的展开性更广,但可归结到用三角形外角性质两次(整合四个角)与最后一个未算的角组合成一个三角形,用内角和即可得五个角的和为180度!思维更上一个高度,不易.进一步展开,六角形、七角形等又如何破解呢?基于此,下面列出的目标要求中最后一个目标可通过第四节课即再上一节习题课来达成!揭示:从"习题题目"呈"课后巩固(阶段要求)".

于是总体归纳出:本节的知识点主体是"三角形的内角和、三角形按角分类、三角形的外角";本节的目标要求是"理解并掌握三角形的内角和等于180度、会应用该性质进行相关计算,掌握三角形的分类、能(在按边分类基础上)从角的角度对三角形进行分类,理解三角形外角的概念、掌握三角形外角的性质、能熟练应用三角形的外角及内角和进行相关计算等".至此,当时给出了如下粗糙的设计.

二、基本设计

1.知识再现

问题:(1)三角形及相关概念?(2)三角形按边分类? (3)三角形的三种重要"线段"?(4)三角形的三边关系?

基本意图:通过温习,创造三角形的研究"环境",做"热身"活动."分类"复习是为本节按角分类的对比铺垫. "三边关系"的复习更是为了过渡的需要,设计为:三角形的研究从两类元素入手,即?(边和角)既然上节已经研究了三边关系,自然本节会研究?点题:三角形三内角的关系(呼之即出)!有什么关系?如何理解?受何启发?进入第二个环节.

2.阅读练习

(1)阅读教科书第46-48页.问题:哪些知识点?相关问题?你的理解?你的困惑?(2)尝试练习,第48页练习1、2、3.

基本意图:通过自学阅读,让学生寻找解决问题的方法,培养自学阅读能力和整体把握文本的能力,给学生一个自由思考的空间去发现、去完善、去质疑;通过练习去验证自学的效果.

3.合作交流

问题(1):你对教材翻折图和剪拼图的操作性理解?如何用数学的眼光看?

意图与思路:(1)揭示"知识点①三角形的内角和性质";(2)翻折操作你试一试,能否一次性完成?数学本质是什么?能否"弱化"一下操作,也达成让三个内角集中在一边上?(引出两个角是通过平行来移动,另一个角"搭便车"也移到了规定的位置!)剪拼操作,你试一试?数学本质是什么?你能绝对肯定一定构成一个平角吗?我们必须怎么做才能让他人相信?(引出证明的必须性);还有其他方法吗?(结合上学期的练习经历和本节的启示)

问题(2):三角形除按边分类外,还有什么分类方法?

意图与思路:(1)揭示"知识点②三角形按边分类的方法";(2)(接上面过渡为)既然三角形内角和为180度,但作为角,单独看,可以是?(锐角、直角、钝角)加入到三角形中,受控于?(三内角和180度)在一个三角形中最多有几个锐角、直角、钝角呢?探究引出第二种分类方法!再让学生自己举出锐角三角形、直角三角形、钝角三角形的具体例子!

问题(3):再次审视第46页剪拼法图2-12(2),你会发现什么?(特殊的现象)

意图与思路:(1)揭示"知识点③三角形的外角性质";(2)(接上面过渡为)上面这些结论的得出,离不开动脑筋图,所以我们再来审视剪拼法图2-12(2),你会发现什么特殊的现象?基于∠ACD的位置与内角∠ACB "两共一反"揭示外角定义、与相邻内角和不相邻两内角的数量特征展开引领揭示外角性质!再变换图式具体理解三角形外角个数与关系等.

4.拓展提升

问题(1):达标练习,教科书第48页练习1、2、3;问题(2):拓展思考,第46页折叠图2-12(1),上面顶点是翻折到一边上,还可以翻折到?(三角形内部、外部)见拓展题图3、图4、图5;若∠A=30°,则∠1+∠2=();一般规律?

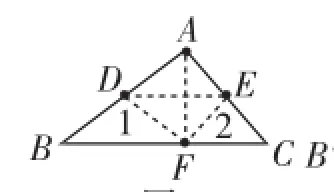
图3

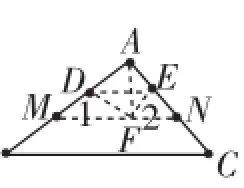
图4

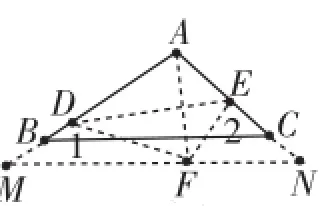
图5

意图与思路:(1)巩固本节知识与方法,书上练习是达成目标,拓展思考是为了发展学生的变式能力;(2)先做基本练习,台上台下互动,展示思路与过程,再依据课本变式,让经典题目找到课本原型,凸显重视课本、开发课本、对比学习的重要性!具体说:重点研究特例图图3,显然原内角∠A=∠DFE.方法1:利用内角和;方法2:连接AF,把∠1、∠2分别看做是△ADF、△AEF的外角,利用外角性质即得∠1+∠2=2∠A;再看图4、图5,一般猜想结论,运用方法1,怎么办?化归法,即过F点作BC的平行线MN交AB、AC两边或延长线于点M、N,构成与图3一样的三角形去做!若用方法2,方法照旧立得!一道阅读探究题立马成型!再从中比较方法的优劣,体会数学思想的魅力,使教学达到一个新的高潮!

5.小结作业

意图与思路:(1)关于小结,由于知识点多、思想方法多、知识联系紧、发散空间大,故仅从知识点、方法点、疑惑点入手更紧凑!(2)关于作业,由于知识容量大,故本节主要进行基本训练,即做第49页A组第4题和第5题、B组第7题;至于提升练习,在下节习题课中呈现!(以上是笔者当时现场的做法,不当之处,恳请同仁指教!)

三、基本结论

(1)有句广告词:疼则不通,通则不痛,说明打通、"活络"筋脉的重要性!教材解读亦如此!窃以为若视高质量的备课是专利成果的话,则有效的课堂教学就是成果的产业化[3](产业化含义:即集知识、思想方法、技能与能力、情感态度、人文素质为一体的数学素养在课堂这条生产线上应运而生)!足见备课设计的重要性.众所周知,备课需备学生、备教法、备学法、备媒体等,但都需与教材内容相匹配,足见解读教材的重要性.

(2)对教材做宏观、微观解读,不仅包括导引、正文文本,还要关注教材后面的各层次的习题,对于"课本内容"[2],我们解读的方法是:先找准新、旧知识联系的中心问题,一般直接来自于文本的导入与过渡语,再围绕之展开从简单到复杂、从基本到组合的问题演绎,即中心问题演绎法,也就是从"课本内容"看"知识体系(前后关联)"、从"课本练习"定"课堂达标(基本要求)"、从"习题题目"呈"课后巩固(阶段要求)".

(3)优化设计(本文略)源于基本设计,而基本设计源于常态下的教材解读,而教材解读乃真实状态下基本功的现实表现,因此,加强常态下的教材解读是教师专业"真实"成长的必修课和必由之路!

1.义务教育课程标准试验教科书.数学(初中)[M].长沙:湖南教育出版社,2014.

2.陈金红."典例导题.问题驱动"案例片段[J].中学数学(下),2013(1).

3.陈金红.你真的看过教材?[J].湖南教育(C版), 2014(12).

4.陈金红,郭作华.改革课堂提升效益成功的"三个方略"[J].数学教学研究,2015(7).

5.陈金红,郭作华.常见但有时不可视而不见[J].教育科学论坛(综合版),2015(8).

6.陈金红,郭作华.你真的看过教材上的习题吗?[J].湖南教育(D版),2015(9).

7.陈金红."理解教材"的灵动思考与教学创新[J].中学数学(下),2013(8).

*本文系全国教育科学"十二五"规划2013年度教育部规划课题FHB130512"生命课堂视野下的教学案例研究"阶段性成果.