"二次根式的运算(第1课时)"课例分析

浙江省象山县象山港书院　周林祥

"二次根式的运算(第1课时)"课例分析

一、背景介绍

《义务教育数学课程标准(2011年版)》(以下简称"课标(2011年版)")倡导过程教育以全面发挥数学的育人功能.但在以浙教版义务教育教科书数学八年级下册第一章第3节"二次根式的运算(第1课时)"为载体的"多人同课异构"式的教研活动中发现,课堂教学普遍存在认知过程短暂(特别是内化过程缺失)的问题,导致学生失去了发展能力与个性及感悟其蕴含的数学思想方法的机会.网上查阅同类课例发现也有类似的现象.基于过程教育的"二次根式的运算(第1课时)"怎样教学?笔者在重复式观课与反思的基础上,将形成的教学经验进行再实践,得到了同仁的认可.现将其整理出来,以飨读者.

二、教学实录

环节1:经历回顾并提出问题的过程---明确研究的问题

师:我们知道,二次根式与分式一样,都是特殊的代数式,因此,二次根式的研究内容和研究方法可以与分式类比.分式研究了哪些内容?

生1:研究了分式的概念、分式的性质、分式的运算、分式的应用.

师:好的.我们已知道二次根式的概念和二次根式的性质,大家认为还应该研究什么?

生2:还应该研究二次根式的运算和应用.

师:好的.二次根式怎样运算?这节课先研究二次根式的乘除运算.(揭示课题)

环节2:探索二次根式的乘除运算---生成二次根式乘除运算法则

师:现在请大家计算下列各题.

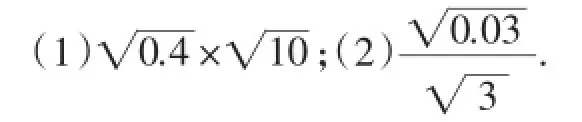
(约2分钟后)

师:谁来展示(1)的计算过程?

师:好的.生3是将小数化为分数后用二次根式的性质进行计算;生4是二次根式性质的逆用.谁来展示(2)的计算过程?

师:好的.生5是将小数化为分数后用二次根式的性质进行计算;生6是二次根式性质的逆用.计算上述各题,用二次根式的性质简单还是逆用二次根式的性质简单?

生7:逆用二次根式的性质简单.

环节3:参与尝试二次根式运算的活动---合作计算有代表性的算式

师:现在请大家计算下列各题.

(待学生尝试计算后)

师:谁来展示(1)的计算过程?

师:好的.谁来展示(2)的计算过程?

师:好的.谁来展示(3)的计算过程?

师:好的.这两种计算过程,尽管采用的方法不同,但策略相同---将其分母有理化.谁来展示(4)的计算过程?

师:好的.一般地,二次根式乘除运算要经历哪几个步骤?

生14:先用二次根式的乘除法则,再化简二次根式.

师:不错.一般地,二次根式乘除运算要经历以下几个步骤:

(1)运用法则,将问题转化为根号内的实数运算;

(2)完成根号内相乘、相除(约分)等运算;

(3)化简二次根式.

师:这是一般方法,有时也可灵活处理(例如(3)).二次根式运算的结果,如果能够化简,那么应把它化简为最简二次根式.下面我们一起来解决下列问题.

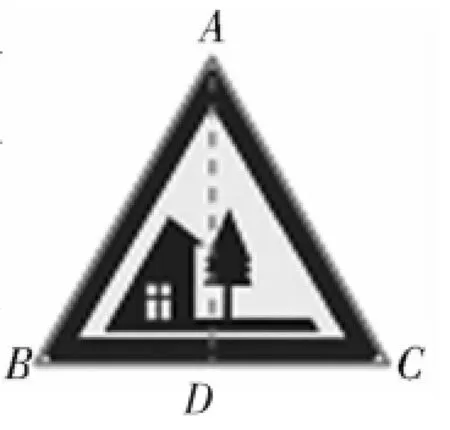
图1

师:要求这个路标的面积,只要知道什么?

生15:只要知道三角形的高.

师:好的.如图1,作AD⊥BC于点D.要求AD,只要知道什么?

生16:只要知道BD.若知道BD,就能用勾股定理求AD了.

师:好的.BD能求吗?

师:好的.谁来陈述解题过程?

师:好的.如果题目没有预定精确度要求,那么结果可以用最简二次根式表示.解决这个问题经历了哪几个步骤?

生19:先结合图形分析求解思路,再书写求解过程.

师:不错.一般地,用代数式解决实际问题的基本步骤是"根据题意画出图形→在图形上标注已知条件→结合图形分析求解思路→用代数式表示未知量→通过有关运算求出未知量".表示与运算是用代数式解决实际问题的思想方法,在表示的过程中经常会用到勾股定理、面积关系等.

(接下来,教师要求学生完成课本中的练习题,并请几个同学在黑板上演示.待学生完成任务后,教师组织学生进行交互反馈与评价)

环节4:参与回顾与思考的活动---合作进行反思与总结

首先,教师出示下列"问题清单",并要求学生围绕"问题清单"进行回顾与思考.

(1)本节课研究了哪些内容?我们是怎样研究的?

(2)一般地,二次根式乘除运算要经历哪几个步骤?

(3)用二次根式及其运算解决实际问题要经历哪几个步骤?

(4)用二次根式或含二次根式的代数式表示未知量有哪些经验?

其次,教师组织学生合作交流,同时教师边倾听、边评价.

最后,在此基础上,教师总结本节课的研究内容与研究方法.

三、教学分析

二次根式的乘除运算法则是二次根式性质的逆用,二次根式乘除运算的方法是需要学生掌握的技术性知识,其具体到抽象的研究方法具有普适性.生成二次根式的乘除运算法则的过程和用二次根式的乘除运算法则进行二次根式乘除运算的过程,有能力发展点、个性和创新精神培养点,其蕴含的归纳思想、化归思想等及用二次根式及其运算解决实际问题的过程和蕴含的数形结合思想、方程思想等,对发展学生的智力有积极的影响."课标(2011年版)"(课程内容)对二次根式运算的教学要求是"了解二次根式(根号下仅限于数)加、减、乘、除运算法则,会用它们进行有关的简单四则运算".教材安排例2的意图是进一步让学生体会代数中的表示与运算的思想方法.目前在这节课的教学中普遍存在生成算法的认知过程短暂和用算法进行运算之后的算理说明过程缺失的问题.本节课根据"课标(2011年版)" (课程内容)对涉及内容的教学要求和教材的教学意图,以有代表性的"题材"为载体,从学生已有的知识与经验出发,运用从具体到抽象的思维策略和教师价值引导与学生自主建构相结合的适度开放的方式,引导学生经历了完整的认知过程.在"回顾并提出问题"的教学中,既有回顾分式研究内容的过程,以通过类比明确二次根式的研究内容,又有类比基础上提出问题的过程,以揭示课题和感悟研究二次根式运算的必要性.在"生成法则"的教学中,既有"计算、比较、归纳"的过程,以生成二次根式乘除运算的法则,又有生成法则之后的教师总结性讲解,以明确二次根式乘除运算的法则是二次根式性质的逆用.在"法则应用"的教学中,既有用生成的法则计算有代表性算式的过程,以巩固法则和发展计算技能,又有计算之后反思的过程,以明确二次根式乘除运算的步骤.在"解决实际问题"的教学中,既有解题之前的分析,以明确求解思路,又有解题之后的反思,以感悟其蕴含的表示与运算的思想方法,积淀用二次根式或含二次根式的代数式表示未知量的数学活动经验.在"回顾与思考"的教学中,既有教师价值引导下学生的思考与交流,又有教师的总结性讲解.这体现了过程教育和以学为中心的思想,也遵循了技能教学的基本规范,能实现"能通过具体算式的计算,感悟逆用二次根式的性质能化简运算过程,并知道二次根式的运算法则是由二次根式的性质得到的;会用二次根式的运算法则进行简单的二次根式的乘除运算,会用二次根式或含二次根式的代数式表示简单问题中的未知量"的教学目标.因此,在算法教学中要实现知识、技能、能力、态度的完美统一,需要教师增强揭示算法所蕴含的思维活动过程的自觉性,而引导学生经历实质性思维过程需要教师贯彻启发式教学思想.以符合"最近发展区"理论的题材为载体,从学生已有的知识与经验出发,运用从具体到抽象的思维策略和教师价值引导与学生自主建构相结合的适度开放的方式,能使学生经历教学过程中的思维站点,从而能促进学生全面、和谐发展.

1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.

2.范良火.义务教育教科书数学(八年级下册)[M].杭州:浙江教育出版社,2014.

3.王伟,邬云德.寓"过程教育"于"二元一次方程"教学探索与点评[J].中学数学(下),2014(2).