反"逼"的课堂更精彩*---以"平面直角坐标系"省优质课为例

南师大附中新城初中　何君青

反"逼"的课堂更精彩*
---以"平面直角坐标系"省优质课为例

近几年国家积极推进新一轮基础教育课程改革,旨在不断加大义务教育阶段减负的力度.可见如何打造初中数学高效课堂,成为数学教师共同探讨的热点问题.当今数学课堂上很多教师常常让学生讨论、交流,或者动手画一画、量一量、折一折,便问学生有何发现,看似探究味十足,但学生其实是被动式地接受知识,不能根本性地发现数学的本质,思维也未得到任何发展.经过多年的探索实践,笔者发现学生的思维在一定程度上不得不"逼",一些简单的问题或直观的结论学生往往是凭借记忆或感觉而得出的,并不能领悟问题的实质,所以教师在教学的过程中需举例正反对比,不停地让学生感觉难以回答,形成认知冲突,于是学生才会积极地在头脑中搜索知识,这样思维碰撞后才能"逼"出最深层的思想,课堂才会有别样的精彩.

2015年11月,江苏省初中数学优质课观摩及评比活动在淮安清江中学举行,笔者有幸作为南京市的代表参加比赛,荣获一等奖,在授课过程中就用到了反"逼"的做法,略有收获,故撰文与同行交流.

一、片段再现

教师:你能描述点P所在的位置吗?(如图1)为了让同学看得更直观,老师在黑板上制作一个类似的模型.

学生1:右上方.

教师:能理解这3个字的请举手.能帮老师解释一下,所谓的右是什么?所谓的上是什么?

学生2:要在黑板上先画两条直线,一条水平直线,一条垂直直线.

教师:(根据学生的描述画出两条相互垂直的直线)有了这两条线作为参照,右上方可以理解了,但右上方的点只有这一个吗?

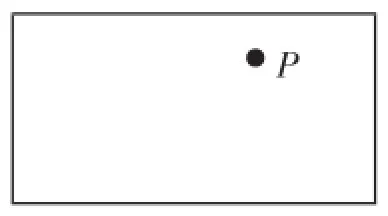
图1

众生:不是.

教师:你能更精确地描述点P所在的位置吗?

学生3:在两条直线上标上刻度,再过点P作两条直线的垂线,将垂足表示的数用有序实数对表示.

教师:(根据学生的描述进行相应的操作)能描述点P所在的精确位置吗?

学生4:(3,2).

教师:再给你一点Q(课前在黑板上确定好大概位置,使P、Q两点关于铅直直线对称),你能精确地描述点Q所在的位置吗?

学生5:和之前一样的方法,(教师操作完成后)可以记为(-3,2).

教师:(继续追问)(-3,2)?这-3从何来的?

学生5:将左边记为负数,不就是-3了?

教师:(继续追问)灵感从何而来?

学生5:数轴.

教师:非常好,有了这个参照物,就能精确地描述点P和Q的位置了,观察一下,说说你对这个参照物的认识.

学生6:它是由两条数轴组成的,而且是垂直的.

教师:观察得很仔细,有了它就可以统一管理平面内的所有点了,数学上将其称为平面直角坐标系,今天就来学习它.(之后介绍平面直角坐标系相关概念)

学生7:(-2,-3).

教师:(继续追问)为什么?

学生7:过点A分别作x轴、y轴的垂线,将垂足对应的实数组合起来形成一对有序实数,所以是(-2,-3).

教师:再给你一点B,请你精确地描述它所在的位置.

学生8:(1,-2).类似的方法,过点B分别作x轴、y轴的垂线,将垂足对应的实数组合起来形成一对有序实数,所以是(1,-2).

教师:也就是说,有了平面直角坐标系,平面内的点就能用有序实数对表示了.

教师:再给你一点C,你能写出与它相对应的有序实数对吗?

学生9:(3,-1).

教师:更一般的,如果Q是平面直角坐标系中的一点,你能确定与它相对应的有序实数对吗?

学生10:过点Q分别作x轴、y轴的垂线,将垂足对应的实数组合起来形成一对有序实数.

教师:反过来,又会怎么样呢?带着疑问一起研究.若给你一对有序实数(3,1),你能在平面直角坐标系中,确定一个与它相对应的点D吗?

学生11:(上黑板画好后再回答)过x轴上表示3的点画x轴的垂线,再过y轴上表示1的点画y轴的垂线,两条垂线的交点即为点D.

教师:再给你一对有序实数(-2,4),你能在平面直角坐标系中,确定一个与它相对应的点E吗?

学生12:过x轴上表示-2的点画x轴的垂线,再过y轴上表示4的点画y轴的垂线,两条垂线的交点即为点E.

教师:通过确定点D、点E的活动,你发现了什么问题?

学生13:有平面直角坐标系后,一对有序实数可以确定一个点的位置.

教师:回顾整个过程,一共总结出了两句话,你能合起来说一遍吗?

学生14:在平面直角坐标系中,一对有序实数可以确定一个点的位置;反过来,任意一点的位置都可以用一对有序实数来表示.简单点说就是建立平面直角坐标系后,平面内的点与有序实数对一一对应.

二、片段解析

此授课片段旨在得到两个结论:其一是构建平面直角坐标系的必要性;其二是建立平面直角坐标系后平面内的点与有序实数对的一一对应.这两个结论的教学都是教师在授课时难以把握的教学环节,教师常常都是直接告诉学生相关结论,再进行练习,让学生加深对其本质的理解,可这样的做法让学生印象不深,不能体会到学习的乐趣.

在体会平面直角坐标系的必要性时,笔者设计的环节充分考虑到学生的认知规律,进行了生动化的教学,首先笔者让学生描述点P的位置,学生很快能想到想要描述点P的位置必须借助参照物,随之在平面中构建两条互相垂直的直线,接着笔者追问:你能精确地描述点P的位置吗?学生想到用距离进行描述,继而再给予一个对称点Q让学生精确描述它的位置,学生的思维被反"逼",感悟到用距离描述会让这两个点的描述方式相同,必须要对这两个点的精确位置加以区分,可以用表示具有相反意义的量进行区别,从而构建出的两条互相垂直的直线"进化"成数轴,构建出了平面直角坐标系的雏形,再通过说一说对参照物的认识过程,让学生亲身经历概念形成的全过程,感受数学概念形成的自然性与合理性,加深学生对平面直角坐标系概念的理解.

在领悟建立平面直角坐标系后,平面内的点与有序实数对一一对应的内涵时,笔者接着上面的研究继续操作,让学生先描述点A的精确位置,此点的作用既是学生巩固之前的描述方法,又是用有序实数对表示点的开始,再让学生描述点B的精确位置,此点的作用是让学生巩固用有序实数对来表示点,之后,笔者配合幽默的语言,让学生迅速感知到平面直角坐标系的作用,自主回答出平面内的点可以用有序实数对来表示,接着再让学生写出与点C相对应的有序实数对,此处的问法和之前不同,上升到规范的语言,进一步让学生掌握在平面直角坐标系中由点的位置写出与它相对应的有序实数对的方法,可以说这3个点缺一不可,每个点都有着不能或缺的作用.随后话锋一转,研究新问题,给学生一对有序实数(3,1),让其在平面直角坐标系中确定一个与它相对应的点D,学生上黑板操作完成后,进行巩固,再给学生一对有序实数(-2,4),让其在平面直角坐标系中确定一个与它相对应的点E,再次反"逼"学生:这个活动又说明了什么问题?使学生感知到建立平面直角坐标系后,一对有序实数可以确定一个点的位置.环环相扣的设计,快速让学生归纳出一一对应的概念,显得十分自然,学生也有很深刻的理解,彻底攻破本节课的难点.

三、教学反思

数学课堂教学要符合学生的认知规律.它不仅包括数学的结果,也包括数学结果的形成过程和蕴含的数学思想方法.教师在课堂教学时要有利于学生体验与理解、思考与探索.课堂教学内容的组织要重视过程,处理好过程与结果的关系;要重视直接经验,处理好直接经验与间接经验的关系.故笔者认为,课堂教学内容的呈现更应注重层次性和多样性,尽可能让学生深刻认识到概念的形成过程,多使用反"逼"的手段是大有裨益的.

在具体操作时,从一节课的开始到一节课的结束都可以问题为核心,不停地根据学生的回答继而追问、反问,用一个又一个的问题"逼"学生展示自己,"逼"学生说出自己的最真实想法,不停地使学生的知识内化,转为生成经验,也"逼"出一节课知识之间的规律.所以无论何时,数学的课堂上不得不反"逼",这样才能探数学之实质,究数学之本质.

*本文系南京市教育科学"十二五"规划立项课题《"跑班"分层模式下初中数学课堂教学与考试评价研究》(课题编号: L/2015/181)的研究成果.

教师:现在再给你一点A(在黑板上任意点出一点),你能精确地描述它所在的位置吗?