能力立意,类比引路,迁移互助---例谈一类正方形动点问题的探究与思考

江苏省太仓市第一中学　朱建良

能力立意,类比引路,迁移互助
---例谈一类正方形动点问题的探究与思考

类比是指数学问题之间及问题本身的条件与结构之间的同与异,矛盾的分析和转化,是对类似的程度进行比较,再寻求突破以使问题得到解决的一种思维方式.类比探究是指对教师创设的问题情境进行变式,如改变条件、改变结论、一般化、特殊化、类比等形式,把数学问题引向更为广阔的数学思维领域,引申出新的更有价值的问题或做出新的发现.

心理学把先前的学习对后续学习的影响称为迁移,美国教育家布鲁纳认为学习的迁移可分为特殊迁移和一般迁移.在教学过程中,一般迁移分为侧向迁移和纵向迁移,侧向迁移指概念、规则或问题解决的方法在新情境中的运用,纵向迁移是指运用已有的概念和规则去解决新的问题.

类比是学习数学的法宝,类比有拨云见日之效,迁移使问题自然过渡,豁然开朗,类比、迁移交互碰撞,使数学思维灵活鲜动,焕发生机.本文以一类正方形动点的中考试题为例,深入挖掘中考试题中蕴含的教学价值,从类比、迁移的角度谈谈几何图形变化的规律,请同行指正.

一、问题启智,类比探究

在例题教学中,充分挖掘问题的内涵,多方位、多角度地在运动变化的状态下化一般为特殊,从"变"认识"不变"的规律,深化对问题的理解,体验数学知识间的联系,揭示问题的本质,实现由侧向迁移向纵向迁移转化,形成理性思维,获得新的发现.

(2014年浙江丽水第23题)提出问题:(1)如图1,在正方形ABCD中,点E、H分别在BC、AB上,若AE⊥DH于点O,求证:AE=DH.

问题解析:证Rt△ABE≌Rt△DAH,则AE=DH.

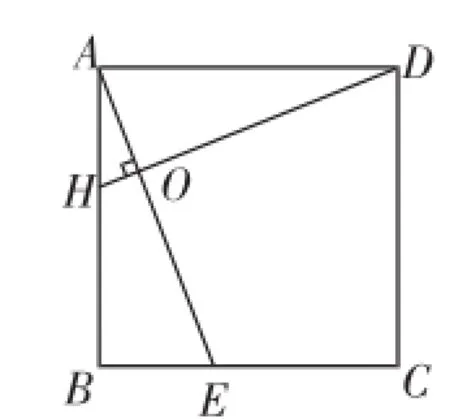
图1

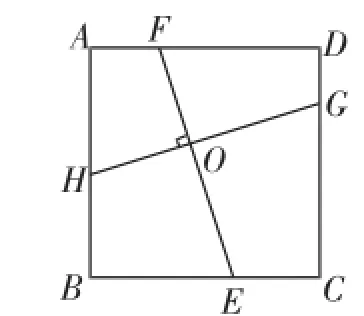
图2

类比探究:(2)如图2,在正方形ABCD中,点H、E、G、F分别在AB、BC、CD、DA上,若EF⊥HG于点O,探索线段EF与HG的数量关系,并说明理由.

问题解析:过G作GN⊥AB于N,过F作FM⊥BC于M,证Rt△GNH≌Rt△FME.如图3,将GH平移至DN处,将EF平移至MA处,依据问题(1)的结论得出DN=AM.

在几何图形比较中理清图形的特征的内在联系,把握两个直角三角形全等的不变因素,通过添加辅助线搬移三角形,构造出相等的线段、相等的角,引导学生学会解读铺垫材料,领悟方法,创造性地纵向迁移知识与方法,另辟蹊径,解决问题.

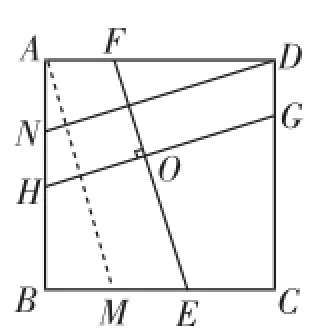
图3

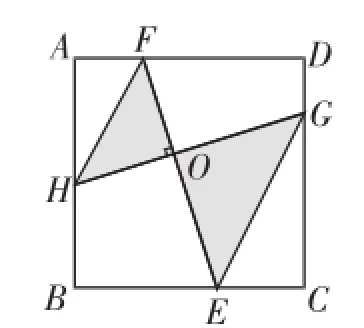
图4

综合运用:(3)在(2)的条件下,HF∥GE,如图4所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.

问题解析:过F作FP⊥BC于P.

面积求解的关键是构造直角三角形,求出线段EF的长度,由两三角形全等迁移至三角形相似,精心设计的面积求解问题,是几何知识内在联系的交叉点,有意识地潜移默化启发学生领悟蕴含于几何图形之中的化归等数学思想,有思维价值的问题导向,引导学生感悟纵向迁移之蕴意,有效地拓展了学生思维的广度和深度.

二、左右逢缘,殊途同归

由上述问题探究两线段数量关系到探究它们的位置关系,同样的问题背景变式探究思维方向,广开思路,在探究思考中获得对正方形动点问题较为全面的体验和理解,侧向迁移、纵向迁移交融,挑战性问题链激活学生的"再发现"思维.

变式1:(2014年山东烟台第25题)在正方形ABCD中,动点E、F分别从D、C出发,以相同的速度在直线DC、CB上移动.

(1)如图5,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE和DF的位置关系,并说明理由.

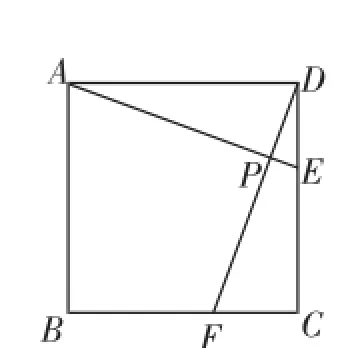
图5

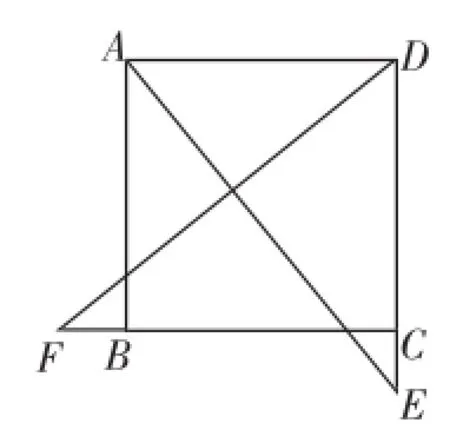
图6

(2)如图6,当E、F分别移动到边DC、CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答"是"或"否",不需要证明)

问题解析:(1)证Rt△ADE≌Rt△DCF,则AE=DF,∠DAE=∠CDF,则AE⊥DF.

(2)成立.

(3)如图7,当E、F分别移动到边CD、BC的延长线上时,连接AE和DF,(1)中的结论还成立吗?请说明理由.

问题解析:延长FD交AE于G,同理可证AE=DF,∠DAE=∠CDF,则AE⊥DF.

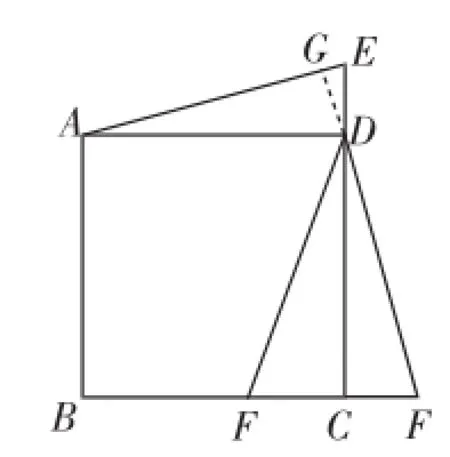
图7

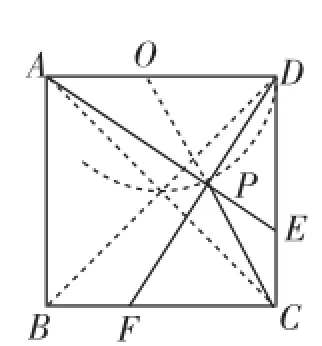
图8

围绕构建全等三角形展开探究,设问的角度创新,辅助线添法没有统一规律,但俗话说:千法万法不如得法,变式1的问题(1)(2)(3)在动态变化中,揭示出几何知识的内在联系,动态演变的几何图形将构建全等三角形的知识技能落实在学生的头脑中,体验了类比思想在数学解题中的应用,促进了知识的深化.

(4)如图8,当E、F分别在直线DC、CB上移动时,连接AE和DF交于点P,由于点E、F的移动,使得点P也随之运动,请你画出点P运动路径的草图,若AD=2,试求出线段CP的最小值.

问题解析:由∠APD=90°,知点P的路径是一段以AD为直径的圆弧,以AD的中点为O,在Rt△ODC中,OC=

探究动点P的运动路径,联想圆中直径所对的圆周角是直角,计算线段CP的最小值,构造直角三角形,转化问题,化繁为简,通过类比,引导学生构造起自己的数学理解力,实现数学知识的再发现,如何添加辅助线就"呼之欲出"了,而不再是"横空出世".以此题为例,引导学生对几何图形的构造有更深刻的认识和体会,反思: (1)如何构造?(2)在什么情况下应添加辅助线构造图形,从而解决问题?(3)添加辅助线的依据是什么?

三、返璞归真,触类旁通

由因导果,知果溯因,在观察、实验、归纳、类比中去猜想、去验证,理解几何动态问题的本质,追根溯源,横向类比,纵向迁移.深入挖掘中考数学试题的教学价值,对同一类问题从不同角度进行变式、延伸和拓展,把类比方法进一步迁移,训练学生的数学思维"同中求异" "异中求同".

变式2:(2014年日照第23题)(1)如图9,在正方形ABCD中,E是AB上一点,F是AD的延长线上一点,且DF= BE,求证:CE=CF.

问题解析:证Rt△CBE≌Rt△CDF,则CE=CF.

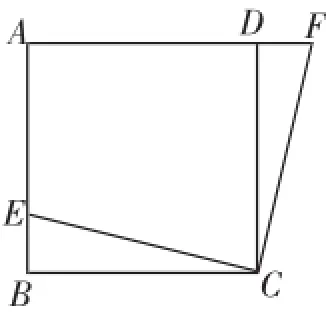
图9

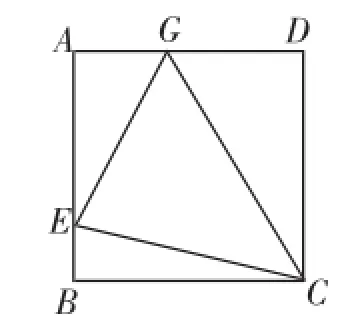
图10

(2)如图10,在正方形ABCD中,E是AB上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.

问题解析:延长AD至F,使DF=BE,连接CF,证Rt△CBE≌Rt△CDF,再证△ECG≌△FCG,则GE=GF,则GE=DF+GD=BE+GD.

引导学生应用转化思想,把复杂的几何图形分解为基本图形,两次构造全等三角形解决问题,较好地建构新知,提炼结论,揭示关键,通过添加辅助线既发展了学生的思维,又使化归思想进一步明朗化.

(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图11,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.

问题解析:过C作CG⊥AD,交AD的延长线于G,证正方形ABCG,则AG=BC,DE=BE+DG,即10=4+DG,则DG=6.设AB=x,则AE=x-4,AD=x-6.在Rt△AED中,由DE2=AD2+AE2,得102=(x-6)2+(x-4)2,解得x=12或x=-2(舍),即AB=12.S梯形ABCD=108.

本题从条件出发"直接补图",外补构造正方形,体现了转化思想,构造直角三角形,将分散的条件集中起来,类比探究,联系勾股定理等知识,找到几何图形的结构特征和条件之间的逻辑通道,使原来较为抽象、隐含的条件清晰地显示出来,进而将问题化繁为简,化难为易.根据问题中的条件与结论,对问题进行再探究的过程是一个思维提升的过程,是增加思维高度和深度的有效学习过程.

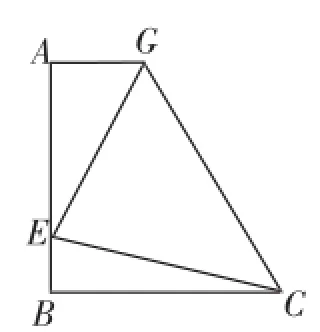
图11

四、教学思考

1."举三反一"---从现象到本质

把正方形情境下动点问题的一种类型的题归纳整理,便于学生在系列探究中挖掘问题及解法的本质联系及规律,同是构造全等三角形,但辅助线添加思路灵活多变,较好地帮助学生通过剖析同一类型的几何问题的解法,归纳其性质,把握问题的核心思想,收到解一题、通一类、会一片的"举一反三"之实效.

多题归一,就是在数学问题的类比、迁移中,发现一条基本的解题思路,就是对一道典型题和多道题的解题思路进一步收敛,以开放度、有层次性、有思维量的问题链形式层层设疑,引导学生自主探究,明白道理,掌握方法,启迪思维.

2.问题驱动---从"变"到"不变"

呈现有意义的动点问题,设置问题有铺垫,层次性强,基于问题驱动探究两条线段的数量与位置关系,求解问题涉及知识和方法不尽相同,有时可以通过具体到抽象、特殊到一般的归纳得到结论,再加以证明,有时可以根据定义和定理,由条件直接进行演绎推理得到结论,有时通过类比、联想先合情推理,再演绎推理求解.随着数学思维层层深入,解剖探讨隐藏在运动变化的几何图形背后的数学本质,拓宽学生分析问题能力的空间,提升学生的思维水平和思维层次,透过正方形的动点问题的表面看出几何图形变化所隐藏的数学思想方法,引导学生以后遇到此类问题"有法可依""有章可循",有思路、有方法.

3.方法引领---从"结果"到"过程"

引导学生会思考,是数学教学的重要目的之一,数学教学不应该是"结果"教学,而应是"过程"的教学,学生以现有的知识结构和研究方法为基础,按照数学知识的结构和内在逻辑的发展趋势,由浅入深、从多角度对问题进行深化过程分析,积累解题策略,有效消除了思维"浅尝辄止"的隐忧,探究既是一种学习方式,也是一个学习过程.

本案例通过专题分类探究,在"变"中寻到一致,在"比"中透出差异,从思维角度聚焦正方形边上动点的变化规律,引导学生经历数学知识"由薄到厚",再经历"由厚到薄"的探究过程,看清问题的本质,学会了思考问题的方法,领悟了解决问题的策略,提升了有效思维水平,深化了学生对类比、化归、转化等数学思想的认识,提升了学生的解题能力,促进了学生数学认知结构的发展和完善.

1.张建良.从"看出"向"证出"提升---一道复习题教学的启示[J].中学数学(下),2013(10).