浅析中考中的三大类特殊图形旋转问题归类剖析

江苏省张家港市第二中学　陈晓芳

浅析中考中的三大类特殊图形旋转问题归类剖析

中学阶段涉及三种基本的全等变换,分别是平移、旋转和翻折.这些全等变换具有如下的基本特征和解决思路:图形在变换前后的基本性质不变,分析这些图形变换时,对给定的图形进行某种位置变化以后,在变化过后的图形中分析有关图形之间的对应关系.这类问题的共同特点是:考查该知识与其他知识之间的联系,解题灵活多变,注重考查学生分析问题和解决问题的能力;结论也相对开放,注重考查学生的推理、猜想、探索能力.

对于三种基本的全等变化,以旋转变换考查的力度最强,出现的相关试题也最多.根据旋转的定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度成为与原来相等的图形叫做图形的旋转,这个定点叫做旋转中心,图形转动的角称为旋转角.图形旋转时,图形中的每一点旋转的角都相等,都等于图形的旋转角.下面就来剖析一下中考中的旋转类问题的几种基本考试模型.

一、正三角形类型

在等边△ABC中,P为三角形内一点,将△ABP绕A点按逆时针方向旋转60°后得到AB与AC重合.通过以上的变化过程,将图1中的PA、PB、PC三条线段变化成图2中的一个△P′CP中,此时△P′AP也应该为等边三角形(正三角形).

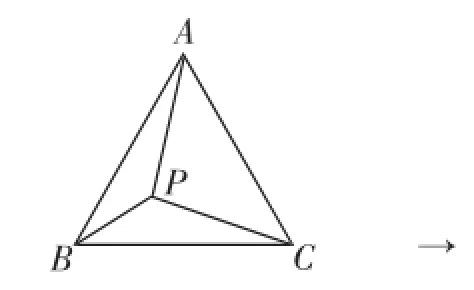
图1

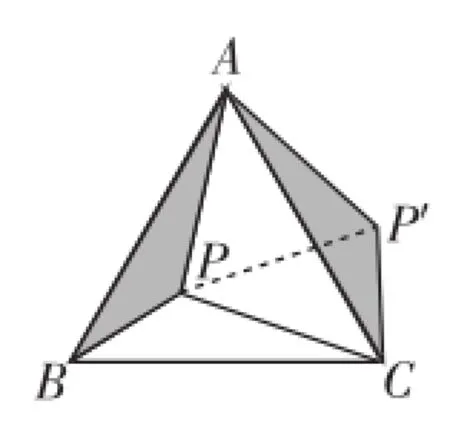
图2

二、正方形类型

在正方形ABCD中,P为正方形ABCD内一点,将△ABP绕B点按顺时针方向旋转90°,使得BA与BC重合.经过如下变化:将图3中的PA、PB、PC三条线段变化成图4中的△CPP′中,此时可以得到等腰直角三角形△BPP′.

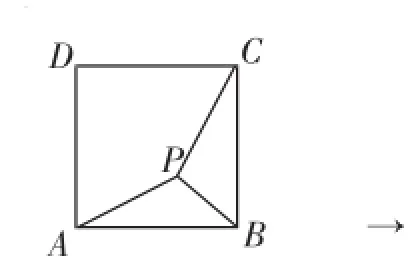
图3

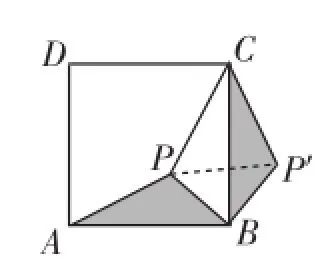
图4

三、等腰直角三角形类型

如图5,在等腰直角三角形△ABC中,∠C=90°,P为△ABC内一点,将△APC绕C点按逆时针方向旋转90°,使得AC与BC重合.经过这样旋转变化,在图6中的一个△P′CP为等腰直角三角形.

图5

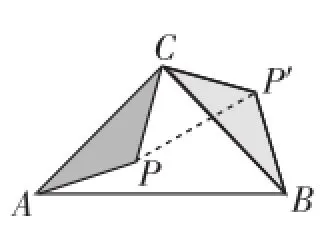
图6

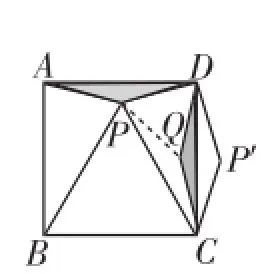
图7

例1如图7,正方形ABCD内有一点P,∠PAD=∠PDA=15°,连接PB、PC,请问:△PBC是等边三角形吗?为什么?

解析:解决问题的关键是得出∠PCD=∠PBA=30°,由前面的分析过程可得,如果将△APD绕点D逆时针方向旋转90°,使A与C重合,这个问题就得到很好的解决了.由此可知,旋转变化作为几何变换中的最常见的变换情况,它一般先会对给定的图形进行相应的旋转变化,通过改变位置产生新的情况,然后在新出现的图形中分析相关图形之间的内在联系,从而揭示出解决问题的一般方法,最终完美地解决问题.

例2(2015年黑龙江省齐齐哈尔市)如图8,在正方形CGEF和正方形ABCD中,点B、C、G在同一条直线上,AE的中点为M,延长DM交EF于点N,连接FM,可得DM= FM,DM⊥FM(证明过程不必书写).

(1)在图9中,当点B、C、F在同一条直线上时,延长DM交EG于点N,其余条件不变,请你思考一下线段FM与DM存在怎样的数量关系和位置关系?写出猜想,并进行证明.

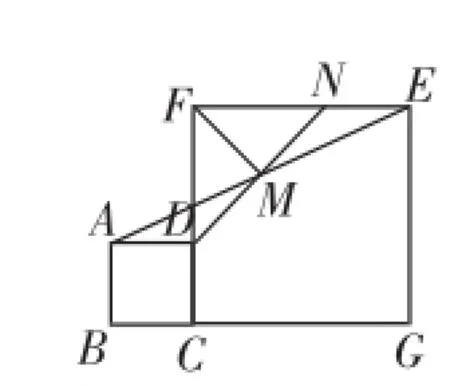
图8

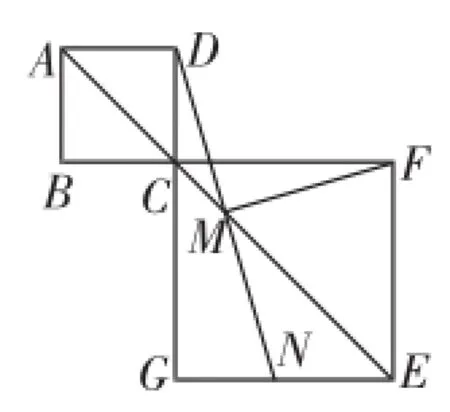
图9

(2)在图10中,当点E、B、C在同一条直线上时,延长DM交CE的延长线于点N,不改变其他条件,探究线段DM与FM有怎样的关系?直接写出你的猜想.

分析:本题考查了图形的证明,涉及正方形的性质、三角形全等的判定及性质,解题的关键是通过构造全等三角形,实现线段的转化及等腰三角形三线合一性质的应用.可以先证明△MAD≌△AEN,得到DM=MN;再证明△DCF≌△NEF,得到DF=FN,应用等腰三角形三线合一的性质得到DM⊥FM.

解:(1)在图9中,关系为DM=FM,DM⊥FM.

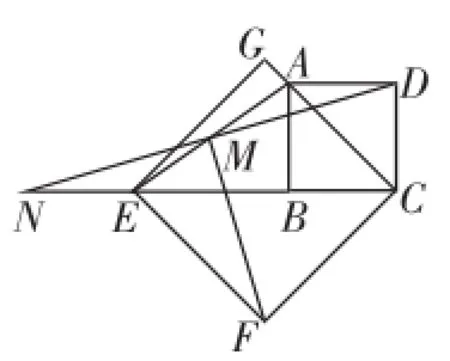
图10

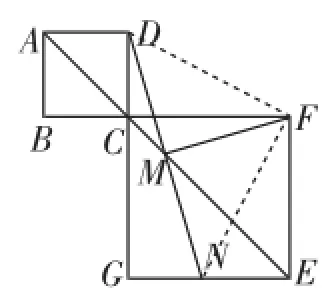
图11

证明如下:如图11,连接DF、NF.

因为四边形ABCD和四边形CGEF都是正方形,

所以AD∥BC,BC∥GE,所以AD∥GE,

所以∠DAM=∠NEM.

因为M是AE的中点,所以AM=EM.

因为∠AMD=∠EMN,所以△MAD≌△MEN.

所以DM=MN,AD=NE.

因为AD=CD,所以CD=NE.

因为CF=EF,∠FCD=∠FEN=90°,

所以△DCF≌△NEF.

所以DF=FN,∠CFD=∠EFN.

因为∠EFN+∠CFN=90°,

所以∠CFD+∠CFN=90°,即∠DFN=90°.

所以DM=FM,DM⊥FM.

(2)图12中,连接DF、NF、MF.

因为四边形ABCD是正方形,所以AD∥BC.

所以∠ADM=∠ENM.

因为M是AE的中点,

所以AM=EM.

因为∠AMD=∠EMN,

所以△MAD≌△MEN.

所以DM=MN,AD=NE.

因为AD=CD,所以CD=NE.

因为∠FCD=∠DCB+∠BCF=90°+45°=135°,

∠FEN=180°-∠BEF=180°-45°=135°,

所以∠FCD=∠FEN.

因为CF=EF,所以△DCF≌△NEF.

所以DF=FN,∠CFD=∠EFN.

因为∠EFD+∠CFD=90°.

所以∠EFN+∠CFD=90°,即∠DFN=90°.

所以△FND为等腰直角三角形.

因为MN=MD,所以DM=FM,DM⊥FM.

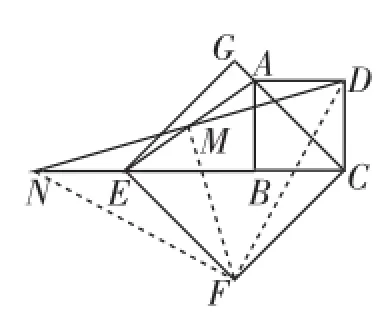
图12

通过以上中考实例的解答,再联系一下图形的旋转思想,是否有更为简单的做法呢?不妨动手试一试.通过这个中考实例,可以看到旋转变化的本质就是抓住变化前后的不变性给予解决.