多角度探究一道硬币自转问题

山东省临沂市第十四中学　李传富

多角度探究一道硬币自转问题

一、问题的提出

例1(2009年广东省佛山市数学中考试题)如图1,将两枚同样大小的硬币放在桌上,固定其中一枚,而另一枚则沿着其边缘滚动一周,这时滚动的硬币滚动了().

A.1圈B.1.5圈C.2圈D.2.5圈

图1

二、问题的探究

解答本题首先要弄清楚自转的含义.自转原本指物体绕着自己的轴心转动,硬币自转指硬币绕着圆心旋转,自转1圈指硬币转360度.

不少人以为自转了一圈,而事实上是两圈.不信,可以拿两枚硬币动手实验一下(硬币我们都有,这个题不会做的时候,我们可以直接从口袋掏出2个硬币自己转一下,答案就出来了.没有硬币也不用沮丧,找两个其他圆形物品,或者直接拿圆规画两个等圆,再剪切一下就可得出).把其中一枚硬币固定(用定圆O表示固定的硬币),另一枚慢慢地沿定圆的圆周无滑动地滚动(用动圆O′表示滚动的硬币),如图2.点A、B、C分别表示动圆O′上位于最下端、最右端和最上端处的点,动圆O′从位置Ⅰ(定圆O的正上方)沿顺时针方向滚动四分之一圆周时,滚动到位置Ⅱ(定圆O的正右方),利用对称性可知此时点B滚动到动圆O′的最左端.再根据点A、B的相对位置可以确定此时点A位于动圆O′的最上端,根据点B、C的相对位置可以确定此时点C位于动圆O′的最下端,根据点A的位置变化(由位于动圆O′的最下端变为最上端)可知此时动圆已滚动半圈(从点C的位置变化也可以看出这点).当动圆O′继续滚动到位置Ⅲ(定圆O的正下方)时,点A又回到动圆O′的最下端,可知此时动圆已滚动一圈.当动圆继续滚动,回到初始位置时,它已滚动了两圈.

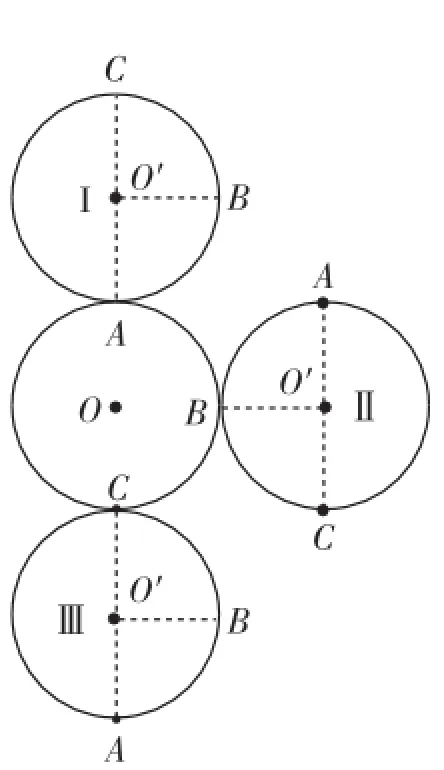
图2

为什么是自转两圈而不是一圈呢?不少人即使面对实验结果仍想不通.还是让我们从2009年河北省的数学中考试卷寻找答案吧.

例2如图3至图7,⊙O均做无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.

阅读理解:(1)如图3,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.

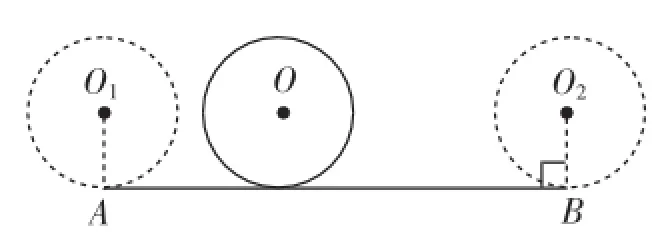
图3

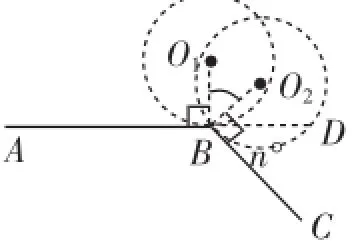
图4

(2)如图4,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的∠O1BO2=n°,⊙O在点B处自转周.

实践应用:(1)在阅读理解的(1)中,若AB=2c,则⊙O自转_________周;若AB=l,则⊙O自转_________周.在阅读理解的(2)中,若∠ABC=120°,则⊙O在点B处自转_________周;若∠ABC=60°,则⊙O在点B处自转_________周.

1位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转_________周.

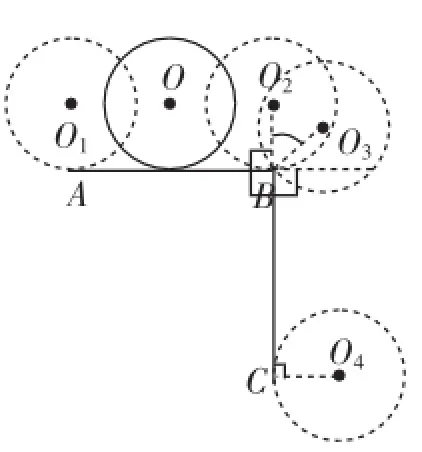
图5

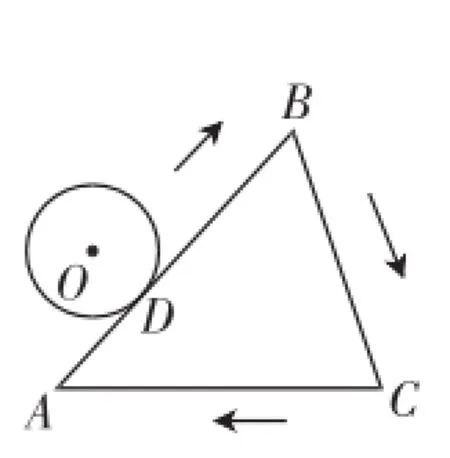
图6

拓展联想:(1)如图6,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.

(2)如图7,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.

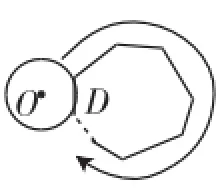
图7

图8

从上面的中考题我们能获得什么启示呢?一枚硬币沿着另一枚硬币的边缘滚动属于硬币在曲线上滚动,解答时比较困难.如果我们将其转化为硬币在直线上滚动,问题就简单多了,这是河北省中考题给我们的一个启示.

如图8,⊙O在直线l上滚动,设⊙O的半径为r,当⊙O自转1圈时,圆心O经过的路径长是2πr;当⊙O自转2圈时,圆心O经过的路径长是4πr;当⊙O自转3圈时,圆心O经过的路径长是6πr;…;当⊙O自转n圈时,圆心O经过的路径长是2nπr.反之,当圆心O经过的路径长是2πr时,⊙O自转1圈;当圆心O经过的路径长是4πr时,⊙O自转2圈;当圆心O经过的路径长是6πr时,⊙O自转3圈;…;当圆心O经过的路径长是2nπr时,⊙O自转n圈.因此,当圆在直线上滚动时,圆心经过的路径的长度等于圆滚动过的长度,圆滚动的圈数等于圆心O经过的路径长除以圆O的周长.

设图1中两枚硬币的半径都为r,硬币滚动时圆心经过的路径长为2π.2r=4πr,而硬币的周长为2πr,所以硬币滚动的圈数为=2.

上面的解答过程实际也用到了一种"以静制动"的解题策略:硬币滚动时,虽然圆上的每点都在运动,各个点的运动规律也不便把握,但硬币的圆心始终在一个固定的圆上运动,这是解答本题的关键.抓住了这点,问题就迎刃而解了.

从图4也可以看出,当把一条长为l的线段AB折过α度角,动圆(半径为r)沿这条直线滚动时,动圆从折线一端A滚动到另一端B时,转了圈多圈.从图7可以看出,如果把长为l的线段AB折成多边形时,动圆沿这个多边形的外周滚动时,从多边形上的某点A开始,回到点A停止,动圆转了1圈加上外角和与360°之比这样多的圈数.而多边形的外角和为360°,所以动圆转了圈多1圈.因此我们可以将圆沿着圆滚动问题转化为圆沿着多边形滚动问题解答,这是河北省中考题给我们的另一个启示.

一个圆可以看成一个边数无限增加的多边形,所以,上面的多边形换成周长为2πr的圆之后,结果也是一样的(如图9).因此若设图1中两枚硬币的半径都为r,则硬币滚动的圈数为+1=2圈.

图9

上面的解答过程实际又用到了一种转化和积分的思想,即圆在曲线上的滚动问题转化为圆在直线上的滚动问题,把圆看成一个边数无限增加的多边形.

方法总结:从上面可以看出,解答硬币沿硬币滚动问题,既可以亲自动手用实验的方法进行解答,也可以将硬币沿硬币滚动问题转化为硬币沿直线滚动问题,根据硬币圆心经过的路径长进行解答,还可以将硬币沿硬币滚动问题转化为硬币沿多边形滚动问题进行解答.其中将硬币沿硬币滚动问题转化为硬币沿直线滚动问题解答方便快捷,一般情况下我们尽量使用这种方法解答此类问题.

三、问题的拓展

原中考题是两枚同样大小的硬币,如果两枚硬币的大小不同,又该怎样计算?

例3如图10,一个小圆币,绕一个直径4倍大的圆片边缘滚动一周,回到原处.试问:在以上过程中,小圆币一共转了几圈?

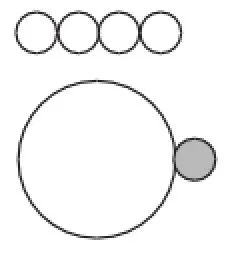
图10

图11

解析:如图11,设小圆币的半径为r,则大圆片的半径为4r,小圆币的圆心绕大圆片边缘滚动一周旋转的路径长为2π.5r=10πr,而小圆币的周长为2πr,所以小圆币滚动的圈数为=5.

例3是小圆沿大圆滚动,如果大圆沿小圆滚动,情况又该怎样呢?

例4如图12,两枚大小不同的硬币⊙O1和⊙O2,其中⊙O1的半径为⊙O2的半径的2倍,⊙O2固定不动,⊙O1沿⊙O2周围滚动,滚动时,两枚硬币总是保持有一点相接触(相切).当硬币⊙O1沿⊙O2周围滚动一圈,回到原来的位置时,硬币⊙O1自转了_________圈.

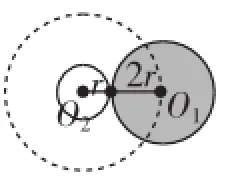
图12

解析:如图12,设小硬币的半径为r,则大硬币的半径为2r,大硬币的圆心绕小硬币边缘滚动一周旋转的路径长为2π.3r=6πr,而大硬币的周长为2π.2r=4πr,所以大硬币滚动的圈数为=1.5.

原中考题是一枚硬币在另一枚硬币的外面边缘滚动,如果是一枚硬币在另一枚硬币的内部边缘滚动,情况又该怎样呢?

例5半径为15cm的小铁环沿着半径为60cm的大铁环的内侧做无滑动的滚动,当小铁环沿大铁环内侧滚动一周回到原位时,问小铁环自身转了几圈?

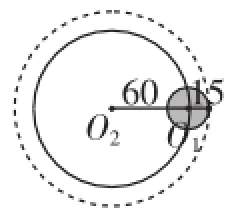
图13

解析:如图13,小铁环的圆心绕大铁环边缘滚动一周旋转的路径长为2π.(60-15)=90πcm,而小铁环的周长为2π.15=30πcm,所以小铁环滚动的圈数为=3.

原中考题是硬币绕一枚硬币滚动,如果绕多枚硬币滚动,情况又该怎样呢?

例6如图14,将4枚半径为1cm的硬币放在桌上,固定其中三枚,而另一枚则沿着它们的边缘从⊙O滚动到⊙O′,这时硬币滚动的路程为________,转了______圈.

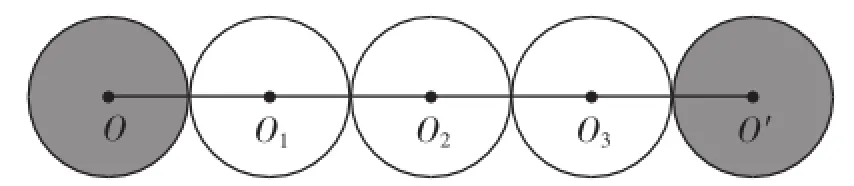
图14

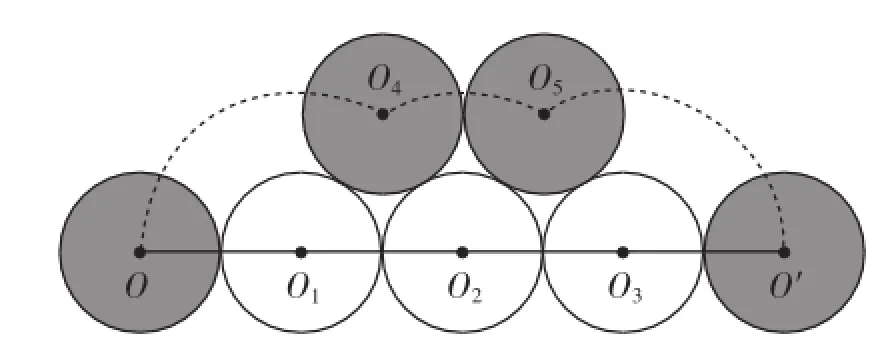
图15

解析:硬币滚动的路径分为三段,如图15所示,从⊙O滚动到⊙O4,其路径是一个半径为2cm,圆心角为120°的扇形,路径长为cm;从⊙O滚动到⊙O,其45路径是一个半径为2cm,圆心角为60°的扇形,路径长为cm;从⊙O滚动到⊙O′,其路径是一个半径为2cm,5

例7如图16,将5枚1元的硬币放在桌上,固定其中四枚,而另一枚则沿着它们的边缘滚动一周又回到原来的位置,这枚硬币自转了_________圈.

图16

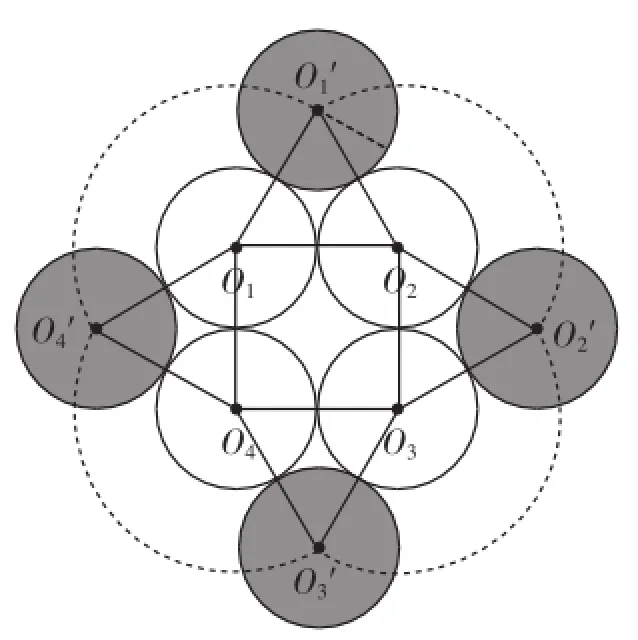
图17

解析:设硬币的半径为r,硬币滚动的路径分为四段,如图17所示,从⊙O1′滚动到⊙O2′,从⊙O2′滚动到⊙O3′,从⊙O3′滚动到⊙O4′,从⊙O4′滚动到⊙O1′,这四段都是一个半径为2r,圆心角为360°-60°-60°-90°=150°的扇形,所以硬币从⊙O1′回到原来的位置滚动的路程l=,而硬币的周长为2πr,所以硬币滚动的圈数为