背景熟悉,方法常规,突出考查能力---2015年陕西中考数学第25题评析

陕西师范大学附属中学　程自顺

背景熟悉,方法常规,突出考查能力
---2015年陕西中考数学第25题评析

一、题目呈现

如图,在每一个四边形ABCD中,均有AD∥BC, CD⊥BC,∠ABC=60°,AD=8,BC=12.

(1)如图1,点M是四边形ABCD的边AD上一点,则△BMC的面积为________.

(2)如图2,点N是四边形ABCD的边AD上任意一点,请你求出△BNC的周长的最小值.

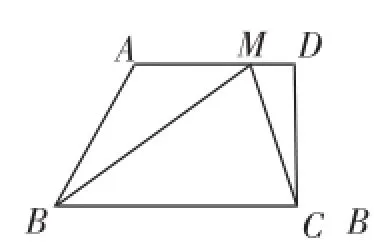
图1

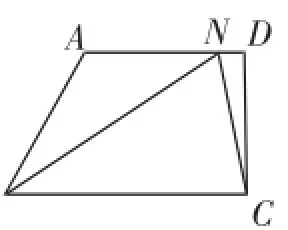
图3

(3)如图3,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.

二、解法评析

1.关于第一问

求△BMC的面积,由于BC=12,故只需求出BC边上的高(即平行线AD与BC之间的距离),比如CD的长,作出梯形的常用辅助线都可以解决,如图4(作高)、5(平移一腰)、6(补成矩形)、7(延长两腰)所示,借助含30°角的直角三角形三边之间的关系计算出高为4姨摇3,进而得到所求面积为24姨摇3,涉及特殊三角形、特殊平行四边形(矩形)等数学知识.由于只是填空,不需要写分析、思考和计算的过程,故节约了考生在此问的作答时间,为解决后续问题提供时间保障.总体来看,该问起点低,入口宽,方法多样,绝大部分学生都能获得成功,为解决后续问题增添了信心!

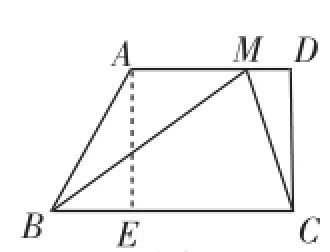
图4

图5

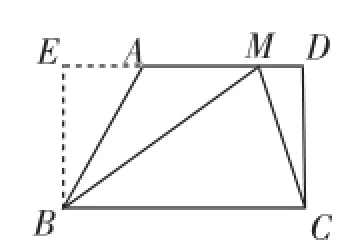
图6

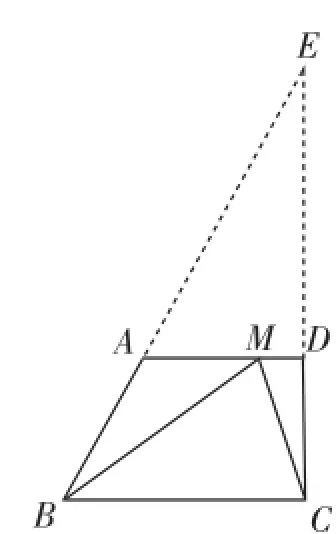
图7

2.关于第二问

求△BNC的周长的最小值,由于BC=12,故只需求出NB+NC的最小值,问题转化成"已知B、C是直线AD外的定点,N是直线AD上的动点,求NB+NC的最小值",即为课本上出现过、学生很熟悉的将军饮马问题:

图8

如图8,延长CD至C′,使得DC′= DC,连接NC′,连接C′B交AD于点N′,连接N′C,则NB+NC=NB+NC′≥C′B=N′B+N′C′=N′B+N′C,所以△BNC的周长的最小值为BC+C′B=

因为D是C′C的中点,且N′D∥BC,所以N′是C′B的中点从而N′C=N′B,即△BNC的周长最小时△BNC为等腰三角形(△BN′C).由第一问知:当点N在边AD上运动时,△BNC的面积不变,故第二问反映了一个事实"在一切同底边并且面积相等的三角形中,以等腰三角形的周长最短."(参考《初中数学竞赛中的平面几何》(周春荔编著)第257页例4),即第二问有等周问题的背景.

将军饮马问题是中考数学的热点,大都以正方形、菱形、圆、平面直角坐标系等为背景,也是学生平时练习中接触的高频题目,对大部分考生而言,该问情境虽新,题意及解法却并不陌生,可以很好地考查学生对数学问题的理解能力和对数学方法的迁移能力.第二问设问简洁、清新,根植于课本,有数学模型可依,有解题方法可寻,难度中等,中等程度及以上的考生即可获得满分,有一定的区分度.

3.关于第三问

在初中,只学习锐角的三角函数,故看到第三问,首先提出的问题是:对于边AD上的任意点P,∠BPC都是锐角吗?事实上,由于4>6,故以BC为直径的圆O与AD相离,如图9,则∠BPC<∠BQC=90°.

关于"是否存在"的回答,可以先计算出三个特殊位置处cos∠BPC的值.如图10,当点P与点D重合时,;当点P与点A重

2XACXBK=S△ABC得,从而cos∠BPC=

进而AK=

;当点P与点N′重合时,同理可求出cos∠BPC=cos∠BN′C=.显然,最后一种情况时

cos∠BPC的值最小.

图9

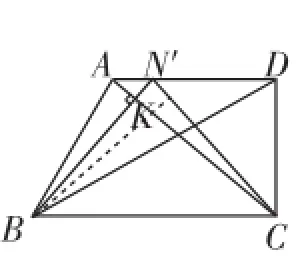
图10

图11

回头来看,点N′其实非常特殊,它是BC的中垂线与AD的交点,如图11,将四边形ABCD补成矩形EBCD,从对称来看,只需考虑点P在N′D上的情况,由计算有cos∠BN′C∠BPC.

如图12,作出△BN′C的外接圆,由O′N′⊥AD知其与AD相切,当边AD上的点P与点N′不重合时,点P都在圆外,有∠BN′C>∠BPC.

此时,还可以换个角度来计算.

方法2:cos∠BN′C=cos2∠BN′O=2cos2∠BN′O-1=2X

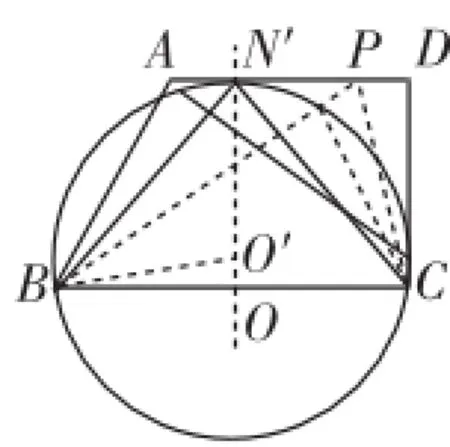
图12

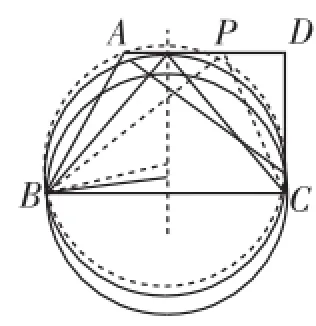
图13

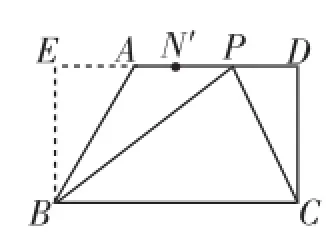
图14

第三问"道是无圆却有圆",涉及"先猜后证"的思想、几何直观(直觉)的能力和探索性思维,是全卷最具选拔性的地方,难度较大,考查学生对数学知识、方法的融会贯通程度和解决问题的创新意识,对学生综合运用所学数学知识、方法、思想和基本活动经验分析问题、解决问题的能力要求较高,具有明显的区分度.

从教师进行研究的角度,不囿于初中的数学知识,还有如下思路.

解法1:由正弦定理有BC sin∠BP C=2R,如图13,当△BPC的外接圆的半径R最小即其与AD相切时, sin∠BPC的值最大,∠BPC最大,cos∠BPC的值最小,计算略.

解法2:如图14,设N′P=a,由余弦定理,得cos∠BPC=.显然,当a=0时(P与N′重合),cos∠BPC取得最小值

解法3:由面积公式有S△BPC=XPBXPCXsin∠BPC,

而面积为定值,所以若∠BPC最大,只需要sin∠BPC的值最大,就需要PBXPC的值最小,由解法2得PBXPC=显然,当a=0时(P与N′重合),PBXPC的值最小,计算略.

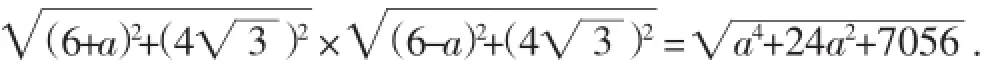
解法4:如图15,B(0,0)、C(12,0),设P(a,4),其中4≤a≤12.

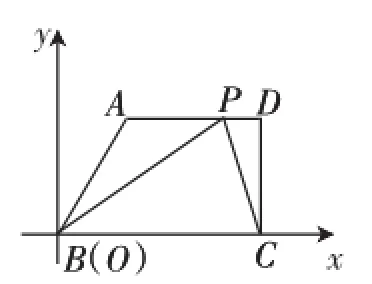
图15

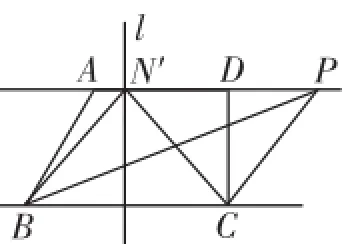
图16

三、思考

第25题以(直角)梯形为载体,研究夹在平行线之间的一边固定的三角形的面积、周长和张角问题,涉及三角形、四边形、圆、勾股定理、三角函数、一元二次方程等众多数学知识,三个小问一气呵成,前后关联.更一般的情况是,如图16,已知AD∥BC,P为AD上的一个动点,有△BPC,明显地,以线段BC的中垂线l为对称轴,即在点N′两侧,存在一对以BC为公共边的全等三角形,故只需考虑l一侧的情况,由于"平行线之间的距离处处相等",故△BPC的面积不变(变化中的不变);直观地可以看到,当点P从"远方"向点N′移动时,△BPC的周长在减小,∠BPC在增大,至点N′处(与点N′重合),△BPC的周长最短,∠BPC最大.退到问题的全貌,有助于整体把握、分析、探索、解决问题,正如华罗庚先生所说,解题时先足够地退,退到我们最易看清楚问题的地方,认透了,钻深了,然后上去,善于"退",足够地"退",退到原始而不失去重要性的地方,这是学好数学的一个诀窍.

本题体现了能力立意的命题思路,背景是熟悉的,要解决的问题是清楚的,求面积(等积变换)、求周长(线段和的最小值)、求最大张角(角的大小比较)分别在课本上都能找到模型和方法,依次为平行线之间的距离、将军饮马问题、与圆周角相关的角的大小比较,因此解决方法也是常规的;问题设计时,由易到难,由定量到定性,从定值到最值,从确定性问题到探索性问题,层层递进,学生对问题的解决也相当于完整地经历了问题提出、发现、分析与解决的研究过程,对学生综合运用数学知识解决新问题的能力,尤其是平时积累的基本数学活动经验的深度考查非常到位.在教学中,建议回归课本,注重基础,加强对数学基本能力的训练,对基本问题进行深入探讨,渗透数学发现与探究的方法,重视数学思维训练和基本数学活动经验的积累.

最后,笔者认为,整个题目的叙述显得臃肿,对边AD上的点的交待有重复,第三问求cos∠BPC的最小值,不指明∠BPC是锐角有些别扭,指明∠BPC是锐角又少了些探索的味道且有方法提示的嫌疑,因此可以进行适当修改,使其更具数学味道.

如图17,在四边形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12,点P是边AD上的一点.

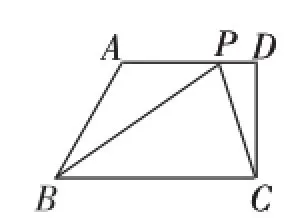
图17

(1)求△BPC的面积;

(2)求△BPC的周长的最小值;

(3)求∠BPC最大时点P的位置.

1.周春荔.初中数学竞赛中的平面几何[M].北京:中国物资出版社,2004.

2.程自顺.以不变应万变,会转化是关键---2013年陕西中考数学第23题阅卷反馈[J].中学数学(下), 2014(3).