"兰利问题"求解的多种途径

山东省临沂市临港经济开发区第四中学　李艳娜

"兰利问题"求解的多种途径

一、问题再现

如图1,△ABC中,AB=AC,∠A=20°,若E在AB上,D在AC上,∠CBD=50°,∠BCE=60°,求∠CED的度数.

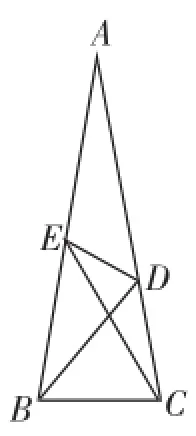
图1

这个问题的历史非常悠久,保守估计也有上百年的历史,其最初的来源现在已经不得而知了.1922年,英国数学家兰利在《数学公报》杂志上发表了一篇题为《一个问题》的文章,向人们详细介绍了这个问题.这可能是该问题第一次正式出现在公众的视野中,因此它也被称为"兰利问题".

第一次看到兰利问题,相信同学们肯定会说"这还不容易",随即拿起身边的铅笔,在草稿纸上涂画起来.不过,大家马上就会发现,仅仅去寻找角度上的数量关系,很快便会陷入僵局.即使将要求的角设为x,列出的方程也无法提供任何有用的信息.事实上,兰利问题远没有那么简单.解决这个问题不仅需要作出不止一条辅助线,而且还要构造出大量新的三角形!不过,虽然解题步骤异常烦琐,但里面所用到的知识点都是大家已经学过的.难怪很多人都把这个问题称为"史上最难的初等几何问题".

虽然这是一道"史上最难的初等几何问题",但用到的知识点都是大家已经学过的,所以我们应该相信经过思考和努力,能够解答这个问题.

亲爱的同学们,你敢向这道难题挑战吗?如果你经过思考和努力,仍然没有破解这道难题,也不要懈气.

二、解法探究

实际上,△ABC是一个比较特殊的等腰三角形,它的顶角为20°,两个底角都为80°,注意到底角与顶角之差为60°,且BC=CD,若以∠ABC为底角,BC为一腰作等腰三角形BCF,并连接DF,这样不仅可以得到一个等边三角形CDF,还可以得到两个等腰三角形CEF和DEF,再求∠CED就方便多了.

解法1:由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.

由∠BDC=180°-∠CBD-∠ACB=180° -50°-80°=50°=∠CBD,得BC=CD.

作CF=BC交AB于点F,连接DF,则CF= CD,∠ABC=∠BFC=80°.

∠BCF=180°-2∠ABC=180°-2X80°=20°.

∠ACF=∠ACB-∠BCF=80°-20°=60°.

则△CDF是等边三角形.则CF=DF,∠CFD=60°.

∠BFD=∠BFC+∠CFD=80°+60°=140°.

∠FCE=∠BCE-∠BCF=60°-20°=40°,∠FEC=180°-∠ABC-∠BCE=180°-80°-60°=40°=∠FCE,则EF=CF.又CF=DF,则EF=DF.

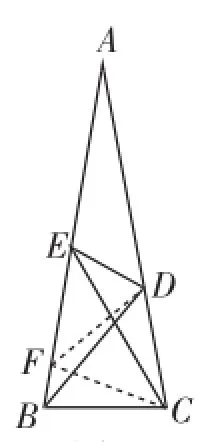
图2

则∠CED=∠DEF-∠FEC=70°-40°=30°.

点评:辅助线CF在本解法中起着至关重要的作用,它沟通了△BFC、△DEF、△CEF和△CDF之间的联系.正如一盘棋赛,看似死局的一方如果走动其中一枚关键的棋子,其他棋子都跟着动起来,全盘皆活.另外我们发现,点F是△CDE的外接圆(该圆半径正好等于等腰三角形ABC的底边长)的圆心,因此在得出EF=CF后,可以确定点F是△CDE的外接圆圆心,由同弧所对的圆周角与圆心角的关系立即可得∠CED=∠DFC=30°.

如果再能注意到BC=CD,联想到正弦定理和余弦定理,若设BC=CD=1,则在△BCE中可以求出CE,而∠DCE=20°,利用余弦定理又可以求出DE之长,然后在△CDE中利用正弦定理求∠CED的度数.

解法2:设BC=CD=1.

在△CDE中,∠DCE=∠ACB-∠BCE=80°-60°=20°.

由余弦定理,得DE2=CD2+CE2-2CD.CE.cos∠DCE= 12+(2cos40°)2-2.2cos40°.cos20°=12+(2cos40°)2-2. 2cos40°cos20°=12+(2cos40°)2-2(cos60°+cos20°)=1+ 4cos240°-1-2cos20°=4cos240°-2cos20°=2(1+cos80°)-2cos20°=2+2cos80°-2cos20°=2+2(cos80°-cos20°)=2+ 2(-2sin50°sin30°)=2-2sin50°=2-2cos40°=2(1-cos40°)= 2.2sin220°=(2sin20°)2.

则DE=2sin20°.

点评:本解法利用正弦定理和余弦定理求解,思路清晰,目的性强,解答的关键是求出DE=2sin20°.

图3

三、改变部分条件探究

如果将兰利问题中的条件"∠CBD=50°"改为"∠CBD=70°",问题中的"求∠CED的度数"改为"求∠BDE的度数",又该如何求解呢?

如图3,△ABC中,AB=AC,∠A= 20°,若E在AB上,D在AC上,∠CBD= 70°,∠BCE=60°,求∠BDE的度数.

已知条件仅将"∠CBD=50°"改为"∠CBD=70°",题目难度大大增加.不过我们可以借助兰利问题及其求解思路助解.解法1:由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.∠BDC=180°-∠ACB-∠CBD=180°-80°-70°=30°,∠ACE=∠ACB-∠BCE=80°-60°=20°.

在∠ABC内部作∠MBC=50°,BM交AC于点M.

∠DBM=∠CBD-∠MBC=70°-50°=20°.

∠BMC=180°-∠MBC-∠ACB=180°-50°-80°=50°=∠MBC.

则BC=CM,∠DBM=∠ACE.

作CN=BC交AB于点N,连接MN、EM,如图4.

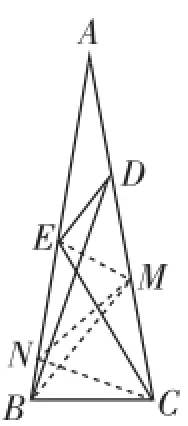
图4

则CN=CM,∠ABC=∠BNC=80°,∠BCN=20°,∠ECN=∠BCE-∠BCN=60°-20°=40°,∠ACN=∠ACB-∠BCN=80°-20°=60°.

则△CMN是等边三角形.则CN=MN,∠CMN=∠CNM=60°.

则∠BNM=∠BNC+∠CNM=80°+60°= 140°.

∠CEN=∠BNC-∠ECN=80°-40°=40° =∠ECN,则CN=EN.

则EN=MN.则∠EMN=70°.

∠EMD=180°-∠CMN-∠EMN=180°-60°-70°=50°=∠BMC.

则∠BMD=∠CME.又∠DBM=∠ACE,则△DBM∽△ECM.

则∠EDM=∠CBM=50°.则∠BDE=∠EDM-∠BDC= 50°-30°=20°.

点评:上述解法借助求解兰利问题的图形及其辅助线,通过两次三角形相似求解,降低了解答难度.这也启发我们学习数学要注意利用已有资源(数学结论、解题方法、思路等)帮助我们解决问题.

如果注意到BC是△BCD和△BCE的公共边,利用正弦定理可以用含BC的式子表示出BD和BE之长,而∠ABD=10°,利用余弦定理可以求出DE之长,然后在△BDE中利用正弦定理求∠BDE的度数.

解法2:设BC=1.

在△BDE中,由余弦定理,得DE2=

即(sin40°DE)2=(sin60°)2+(2sin80°sin40°)2-2. sin60°.2sin80°.cos10°.sin40°

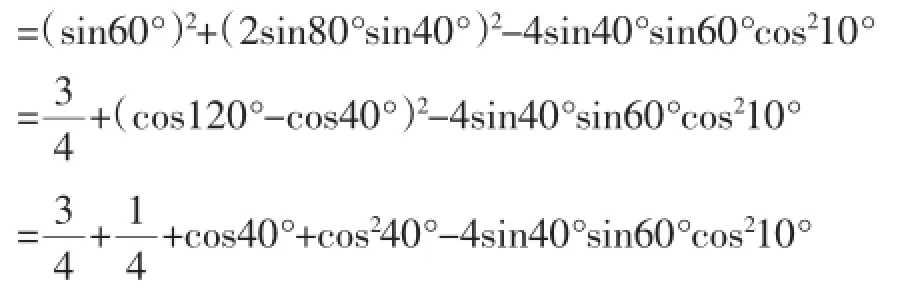
=1+cos40°+cos240°-4sin40°sin60°cos210°

=2cos220°+cos240°-2sin40°sin60°.2cos210°

=2cos220°+cos240°+(cos100°-cos20°)(1+cos20°)

=2cos220°+cos240°+cos100°-cos20°+cos100°cos20°-cos220°

=cos220°+cos240°+cos100°-cos20°+cos100°cos20°

=cos220°++cos80°)

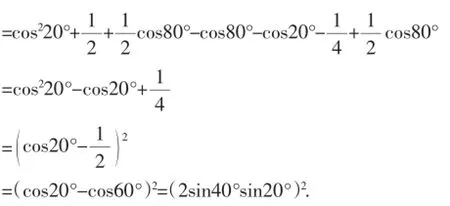
则sin40°DE=2sin40°sin20°.则DE=2sin20°.

则∠BDE=180°-∠ABD-∠BED=180°-10°-150°= 20°.

四、弱化条件探究

如果将兰利问题中的条件"若E在AB上,D在AC上,∠CBD=50°,∠BCE=60°"改为"在AB上取一点D,使AD= BC",问题中的"求∠CED的度数"改为"求∠ACD的度数",又该如何求解呢?

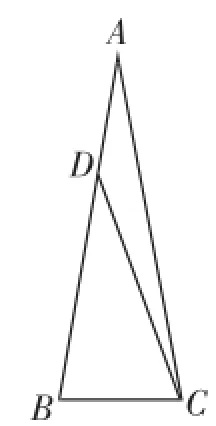
图5

图6

如图5,△ABC中,AB=AC,∠A=20°,在AB上取一点D,使AD=BC,求∠ACD的度数.

为了利用条件"AD=BC",可以BC为边构造等边三角形,并连接AE,借助全等三角形求解.

解法1:如图6,以BC为边构造等边三角形BCE,连接AE.

由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.

易证△ADC≌△CEA,则∠ACD=∠EAC=10°.

当然,由AD=BC,可设AD=BC=1,然后在△ABC中,利用正弦定理求出AC,在△ACD中,利用余弦定理求出CD,在△ACD中,利用正弦定理求∠ACD的度数.

解法2:设AD=BC=1.

在△ACD中,由余弦定理,得CD2=AD2+AC2-2AD. AC.cosA

=12+(1+2cos20°)2-2(1+2cos20°)cos20°

=1+1+4cos20°+4cos220°-2cos20°-4cos220°

=2+2cos20°=2(1+cos20°)

=2.2cos210°=(2cos10°)2,则CD=2cos10°.

则sin∠ACD=sin10°.则∠ACD=10°.

可以看出,兰利问题及根据兰利问题改编的问题(一般都是竞赛题),都可以利用初中方法和高中方法求解,利用初中方法求解需要作的辅助线一般不少于两条,而且辅助线的作法非常巧妙,不容易想到.而利用高中三角知识求解思路清晰、解题目标明确,但在利用余弦定理求某一线段长时难度较大,不仅运算量大,而且需要对三角知识掌握得比较娴熟.可见利用初中方法和高中方法解决兰利问题及根据兰利问题改编的问题各有千秋!