一道填空题的高零分率引发的思考的再思考

浙江省德清县三合中心学校　沈国

一道填空题的高零分率引发的思考的再思考

原题:如图1,在平面直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿x轴的正方向移动,点B在∠xOy的平分线上移动,则点C到原点O的最大距离是_________.

图1

图2

在文1中朱玉祥老师重点分析了该题的高零分率的原因,主要探究了该题的命题者是怎样一步步赋予它如此高的难度.朱老师从该题的"源头"梯子滑动问题开始,到变换角度求△AOB的最大面积,再到求一个顶点与原点的最大距离,最后变换到A、B两动点放在锐角的两边上滑动,清晰地展现了该题是如何一步一步变化过来的,难度是如何一点点上升的.笔者阅读之后受益匪浅,十分赞同朱老师的观点,作为一道填空题的压轴题,学生如果没有经历过这样一个试题改编的过程,不借助"梯子"是很难一步跨越的.

文1中原题的答案如下所示.

如图2,连接OC,交AB于E,当OC⊥AB时,OC有最大值(理由如题3).此时OC也平分AB,且∠ACE=30°.

设OA=OB=x,作BF⊥OA,垂足为F.

在Rt△BOF中,因为∠BOF=45°,所以BF=OB.sin45° =xX.在Rt△AFB中,因为AF2+BF2=AB2,所以

文1中的题3及其解题思路如下所示.

(2009.山东)如图3,已知边长为a的正三角形ABC,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC的长的最大值是_________.

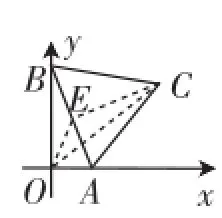
图3

连接OC,取AB的中点E,连接CE、OE,如图3,显然OC≤OE+CE,而OE与CE的和是个定量,所以当A、B在滑动中使OC经过点E,也就是OC=OE+CE时,OC的长度最大.此时,△AOB为等腰直角三角形(面积最大),所以,而△ABC是等边三角形,AB=a,所以OC的最大值为

笔者阅读完原题的答案及题3的解题过程后,对原题答案中的"当OC⊥AB时,OC有最大值(理由如题3)"这句话产生了几点疑问.

疑问一:当OC⊥AB时,OC是否最大?

疑问二:"理由如题3",这样说理学生能接受吗?这两道题是属于本质相同的问题吗?

疑问三:有没有更好的方法,有没有能让学生接受并可以理解的方法?

笔者对这三个疑问的思考如下所示.

对于疑问一,笔者好像无法根据题3的解题思路来证明,只能借助几何画板来证实当OC⊥AB时OC确实最大(如图4).

OC=4.07611厘米OC=4.13981厘米OC=4.09916厘米

图4

对于疑问二,笔者认为题3的说理过程学生能理解,也能接受,因为依据的是三角形三边的关系,即三角形中两边之和大于第三边,但是能否用此来作为原题中OC取得最大值的依据,笔者认为值得商榷.题3中OC≤OE+CE,且OE与CE都是定值,当O、C、E三点共线时OC最大.而原题中(如图5),OC≤OE+CE,但OE是个变量,为什么三点共线时OC最大呢?对于这点,朱老师好像没解释清楚,只是说题3中OC取得最大值时△AOB为等腰直角三角形(面积最大),然后朱老师就认为原题中OC取得最大值时△AOB也为等腰三角形.笔者认为这样说理不科学,依据的是一种解题经验,而不是真正意义上说理的依据.这里学生即便做过题3,且能找到OC最大时的位置,如果让他马上做原题,我相信绝大部分学生还是束手无策,即使能做对也是猜对了OC取得最大值时的位置,至于为什么此时OC最大他也说不清楚.

那么这两道题的本质是否相同?应该说原题是题3的一个变式,题3是一种特殊情况,原题是一般情况,但是这种变式已经改变了点E运动的轨迹,题3中点E运动的路径是圆弧(如图6),而原题中点E运动的路径则是椭圆(如图7),虽然圆是椭圆的一种特殊情况,但是在这里当OC取得最大值时用同样的说理过程好像不够严密.可能朱老师站的角度还要高,能一下子就洞察到这两种情况的本质是一样的,但是我们又该如何面对我们的学生呢?接下来就是笔者对疑问三的思考.

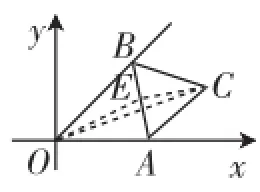
图5

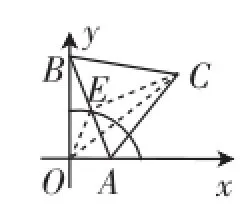
图6

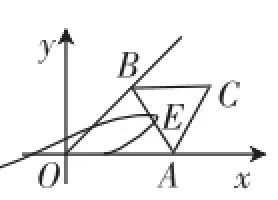
图7

题3是抓住了AB的中点E找到了解题的突破口,利用同样的方法来解决原题则不行,既然两道题是属于本质相同的题目,那么这两题肯定有相通的地方.笔者注意到虽然原题做了适当的改编,但是也有相同的地方,即两道题中AB的长是定值,以及在边AB运动的过程中其所对的角度也都一直没变,这样笔者就想到了可以通过构造辅助圆来解决原题.因为我们知道,当一个三角形的一边长不变,其所对角度也一定时,这个三角形的外接圆的半径是不变的.这样解决原题就更简单了,如图8,构造△AOB的外接圆⊙H,因为圆周角∠AOB=45°,所以圆心角∠AHB=90°.因为AB=2,所以AH= BH=.连接CH交AB于E,进一步可得CH⊥AB于E,所以EH=1,CE=,所以CH=1+.因为OC≤OH+CH,而OH与CH的和是个定值,所以当O、H、C三点共线时,OC的长度最大,即OC=OH+CH=1++.

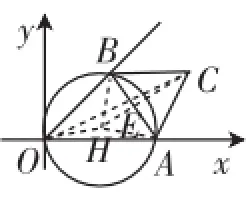
图8

对于这种方法,学生只要能理解⊙H的大小不变,后面的解题过程理解起来应该没问题.这种解法跟题3的解法是一样的,这种方法才是这两道题的通法,只不过题3中,点E和△AOB的外心是互相重合的,且点E又刚好是AB的中点,由于思维的定势,做原题时学生也会先去找AB的中点,由于OE的长是变化的,所以就没法往下做了,阻断了学生的思路.题3中可以根据直角三角形斜边上的中线等于斜边的一半确定OE的长不变,没有必要画出辅助圆,所以做原题时学生没有这方面的经验,也就想不到要构造辅助圆,从而就不能像题3一样将OC的长转化成小于或等于两条固定线段长度之和,就找不到解决问题的突破口,正是由于这些原因,才真正导致原题这么高的零分率吧.根本原因是学生对于构造辅助圆的问题不够熟练,所以我们在平时教学中,还是应该让学生多关注一下这类题目,如下面的两道很有新意的题目.

题目1:(2010.德清县自主招生)今有一副三角板(如图9),中间各有一个直径为4cm的圆洞,现将三角板a的30°角的那一头插入三角板b的圆洞内(如图10),则三角板a通过三角板b的圆洞的那一部分的最大面积为_________cm2.(不计三角板的厚度,精确到0.1cm2)

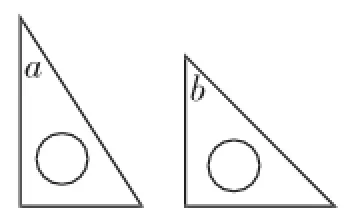
图9

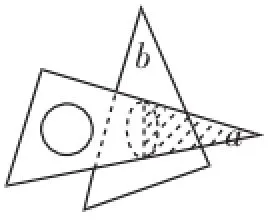
图10

题目2:(2014.武汉模拟)如图11,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为().

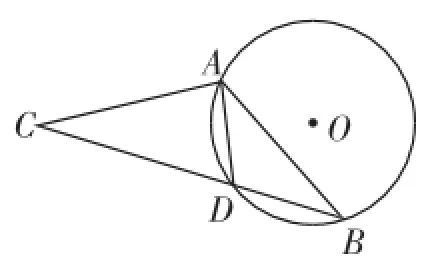
图11

总之,在教学中,我们要引导学生用数学的眼光去审视问题、探究问题,高度把握数学题的本质.在学生认知和技能的最近发展区的基础上,通过变式、类比对习题进行再研究,寻求问题的增长点,从而达到做一题、会一类、通一片.同时我们也要关注学生分析问题的思路,关注推理的严谨性,关注合理表述、规范书写,从而提高教学的有效性及针对性.

1.朱玉祥.一道填空题的高零分率引发的思考[J].中学数学教学参考(中),2014(4).

2.朱松林.变式延伸从最近发展区开始[J].中学数学(下),2013(1).

3.杨绍平.贵有解题思路重在推理严谨---南京市2013年中考数学第25题评析[J].中学数学(下), 2013(9).