定积分的几何意义在定积分计算中的应用

杨磊，景宇哲

（1.大连财经学院基础部，辽宁大连116000；2.大连经济技术开发区第一中学，辽宁大连116000）



定积分的几何意义在定积分计算中的应用

杨磊，景宇哲

（1.大连财经学院基础部，辽宁大连116000；2.大连经济技术开发区第一中学，辽宁大连116000）

摘要：利用定积分的几何意义计算定积分，使计算化繁为简，拓宽了解题思路.

关键词：定积分；几何意义；不等式

1　定积分的几何意义

定积分起源于求不规则图形的面积和体积等实际问题.古希腊的阿基米德用“穷举法”，我国的刘徽用“割圆术”，都曾计算过一些几何体的面积和体积，这些均为定积分的雏形.直到17世纪中叶，牛顿和莱布尼兹先后提出了定积分的概念，并发现了定积分与微分之间的内在联系，给出了定积分计算的一般方法，从而才使定积分成为解决有关实际问题的有力工具.

定积分的概念是一个教学难点，因为定积分是一个特殊的极限过程，与之前的数列极限和函数极限有很大区别.阐述定积分概念的经典引例是求曲边梯形的面积，而这个引例很好地阐述了定积分的几何意义.通过定积分的几何意义，把一个抽象的定积分运算与形象的几何图形结合在一起，使学生对概念的理解更加深刻.因为定积分的性质都可以用它的几何意义进行很好的解释，所以繁琐的定积分计算和定积分的抽象证明，都可以试着从它的几何意义这个角度来考虑问题，往往会得到简便快捷的解题方法.

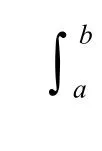
图1定积分的几何意义

由定积分的几何意义可以看出，定积分的值等于由被积函数所围图形面积的代数和.如果已知被积函数的图像，由此曲线所围的图形是规则的或是可以通过“割补法”凑成规则图形，那么定积分也可以从被积函数所围的几何图形的面积中求得.

2　利用定积分的几何意义求定积分

例1［2］设a＞1，求证：.

方法1求证的等式左侧直接通过积分的计算方法，利用牛顿-莱布尼兹公式可以得到等式右侧的结果.

方法2等式左侧第1个积分的被积函数为y=lnx（1≤x≤a），积分变量是x，第2个积分的被积函数为x=ey（0≤y≤lna），积分变量是y.通过观察，这2个被积函数互为反函数，它们的图像是同一条曲线，并且积分上、下限均对应彼此的定义域（见图2）.根据定积分的几何意义，由曲线lnx，x=1，x=a及x轴所围的图形与由曲线ey，y=0，y=lna及y轴所围的图形正好组合成一个矩形，而矩形的面积等于这2个定积分的和.

证明阴影矩形的面积等于aln a，矩形被分成A和B 2部分（见图2），A的面积等于，B的面积等于，于是得到=alna.

可以将这个具体的结论推广到一般情形.

命题［3］设函数y=f（x）在区间［a，b］（0＜a＜b）上非负且单调增加，反函数为x=f-1（y），则有（y）dy=bf（b）-af（a）.

证明因为f（x）与f-1（y）互为反函数，而［a，b］和［f（a），f（b）］分别是函数f（x）的定义域和值域（或反函数f-1（y））的值域和定义域），函数f（x）与f-1（y）的图像是同一条曲线（见图3）.因此，f（x）与f-1（y）在各自区间上定积分的和等于阴影部分的面积，阴影图形的面积等于bf（b）-af（a），即（y）dy=bf（b）-af（a）.

这一类定积分的特点是被积函数单调递增，存在反函数.函数f（x）与其反函数f-1（y）的定积分的和可以转化成求规则图形的面积.

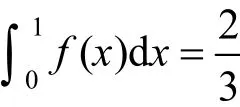
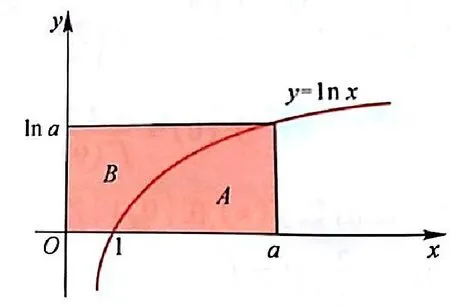
图2例1题解图示

图3命题图示

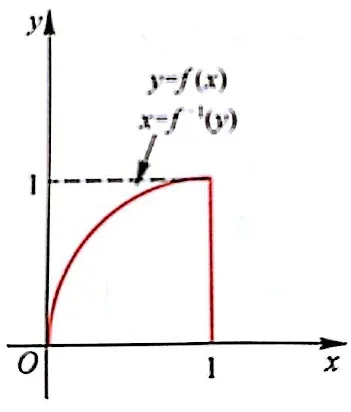
图4例2题解图示

3　利用定积分的几何意义证明不等式

在不等式的证明中，可以根据不等式中函数的特点，结合定积分的几何意义，提供一些解题技巧，使证明变得简单.

例4［4］若a＞b＞0，求证：ln a-ln b .

图5例3题解图示

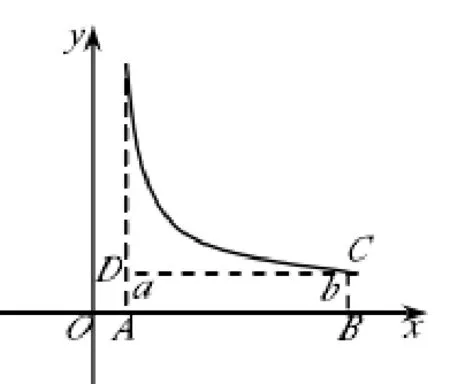
图6例4题解图示

图7例5题解图示

可以看出，定积分的几何意义可以将复杂、抽象的函数关系变得简单、直观.而解决不等式证明的关键就在于将不等式的一端函数转化成曲边梯形的面积，另一端函数转化成规则图形的面积（如矩形、三角形和直边梯形等），然后再利用熟悉的方法来解决问题.根据函数表达式的特点，利用定积分的几何意义可以把问题的数与形很好地结合在一起［5-8］.

参考文献：

［1］张顺燕.数学的思想、方法和应用［M］.北京：北京大学出版社，2002：332

［2］王志超.高等数学轻松学［M］.北京：北京航空航天大学出版社，2015：109

［3］郭镜明，韩云瑞，章栋恩，等.美国微积分教材精粹选编［M］.北京：高等教育出版社，2012：123-126

［4］王建娥.定积分的几何意义在中学数学中的应用［J］.福建中学数学，2010（12）：14-15

［5］吴赣昌.高等数学［M］.北京：中国人民大学出版社，2009：152-153

［6］刘兴薇.关于定积分概念和性质的应用研究［J］.科技资讯，2013（25）：208-210

［7］郑玉军.定积分中两个公式的推广与应用［J］.湖南科技学院学报，2015，36（5）：25-27

［8］罗威.定积分计算中的若干技巧［J］.沈阳师范大学学报：自然科学版，2010，28（2）：165-168

The application of the geometric meaning of definite integral in the definite integral calculation

YANG Lei，JING Yu-zhe
（1. Department of Basic Course，Dalian University of Finance and Economics，Dallian 116000，China；2. No.1 Middle School of Dalian Economic and Technological Development Zone，Dalian 116000，China）

Abstract：Researched the calculation of definite integral using the geometric meaning of the definite integral，it make the calculation simple，increase the problem solving methods.

Key words：definite integral；geometric meaning；inequation

中图分类号：O175.12∶G642.0

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.015

文章编号：1007-9831（2016）05-0051-04

收稿日期：2016-03-04

基金项目：黑龙江省高等教育教学改革项目（JG2014010966）

作者简介：杨磊（1979-），女，黑龙江哈尔滨人，讲师，硕士，从事计算数学研究.E-mail：dfxyjcbyl@126.com