化归在独立院校高等数学课程教学中的应用

刘伟

（天津师范大学 津沽学院，天津 300387）



化归在独立院校高等数学课程教学中的应用

刘伟

（天津师范大学 津沽学院，天津 300387）

摘要：高等数学是独立院校理工类专业的必修课程，但是独立院校学生的数学基础相对薄弱.研究了如何利用化归思想提高独立院校高等数学课程的教学质量.

关键词：化归；极限；泰勒公式；反常积分；高等数学

高等数学是独立院校理工类专业学生的必修课程，但是独立院校学生的数学基础相对薄弱.虽然目前国内出版了针对独立院校理工类专业使用的高等数学教材，但是不同院校不同专业学生的差距较大.因此，教师在教学过程中，不能拘泥于教材，要充分了解学生的情况，对教材的内容进行适当的取舍或加工，采用适合学生特点的教学方法进行教学.

独立院校学生基础较薄弱，教师在课堂教学中重视数学思想方法的传授［1］，有助于学生更好地理解和掌握所学知识.由于种种原因，很多独立院校高等数学课程的课时非但没有增加，反而减少.虽然很多针对独立院校编写的高等数学教材已经对知识进行了精简，但是实际教学中依然很难将课程知识全部讲完.

因此，教师在教学中应改变教学观念，从教知识转变到教数学的思想方法，注重培养学生的数学思维.即使课程内容不能讲完，但是学生掌握了思想方法，在课下自学时就会容易得多.本文针对独立院校的特点，研究了化归思想在高等数学教学中的作用.

1　化归的含义及作用

化归既是人们思考或解决问题的基本方法，也是一种数学的思维方式.善于使用化归是数学家思维方式的重要特点，也是其在思维方法上的独特之处［2］.

化归是转化和归结的简称，其基本思想是：人们在解决问题时，常常是将待解决的问题A，通过某种转化手段，归结为另一个问题B，而问题B是相对较易解决或已有固定解决程式的问题，且通过对问题B的解决可得到原问题A的解答［3］.

化归方法和逻辑演绎方法是数学家特别重视的2种方法，原问题的解和新问题的解之间具有十分明确的逻辑关系和数学关系，通过化归可以很快地找到问题解决的思路［4］.

在教学中渗透化归思想有十分重要的意义.但是化归作为一种数学思想方法，在教材中体现的并不像概念和定理等那样明显，如果教师不在教学中去渗透，学生很难对化归思想有着深刻的理解，因此教学中要加强对化归思想的渗透与训练.

高中所学习的解析几何内容就是化归方法应用的典范，解析几何是将几何问题转化为代数问题.但是化归不仅限于解析几何，如解二元一次方程组是通过加减消元法或代入消元法化为一元一次方程.初学一元二次方程时，并不是先讲公式解法，而是通过配方法将其化为2个一元一次方程的乘积，进而进一步求解.这些问题的解决，都体现了将新问题转化为已解决问题的方法，也就是化归方法.数学史上的经典问题或重大创造，很多都是利用化归方法，如解析几何及尺规作图三大难题的解决.可以看出，数学知识的学习，就是不断将新问题化归为已解决问题，只不过在转化过程中往往需要用到很多技巧等.化归正是新知识与旧知识之间的桥梁，学生掌握了化归方法，对于理解知识，优化其数学认知结构都有很大的帮助.

2　化归在高等数学教学中的应用

对于高等数学知识而言，学生初学时往往感觉到知识内容抽象，难度大，不易理解.从化归的角度来看，这是因为学生面对新知识时，往往看到的是书上一个个抽象的概念和定理，不能用化归的方法找到新知识与旧知识间的联系，将新旧知识割裂开来，造成了学习上的困难.因此，教师在教学过程中更应注重利用化归来帮助学生搭建起新旧知识间的桥梁，提高教学效率［5］.

2.1 极限教学

求极限经常需要复杂的恒等变形，学生在解题过程中往往感到题目常做常新.教师在教学过程中固然要重视各种题型的讲解和训练，但是也要重视相关性质和定理的教学.仔细阅读教材，可以发现教材的编排很好地体现了化归的思想，新问题总是转化为已解决的问题.只是作为教科书，化归的思想是隐藏在字里行间，没有明确地写出来.而教师在教学过程中正是要将这一点告诉学生，这样学生才能明白教材的编写意图，这也有利于帮助学生建立良好的认知结构，同时掌握研究数学问题的方法.

以针对独立院校理工类专业编写的《高等数学》［6］46为例，教材中以例题的形式证明了，并不加证明地给出了，但教材中并没有指出为什么这样安排.作为教师要明确，有了，，，利用极限的四则运算法则、复合函数的极限及无穷小量性质等，就可以将很多极限问题转化成这3个已经解决的问题.

2.2 泰勒公式教学

泰勒公式一直是高等数学课程中的教学难点.泰勒公式的实质是利用多项式函数对足够光滑的函数进行局部逼近［8］.其教学主要有2个难点，一是学生不了解n次多项式函数.这是由于中学数学课程中并没有对3次以上的n次多项式函数进行深入研究，所以刚进入大学阶段的学生对于n次多项式函数的光滑性以及图像的走势一无所知.二是学生在之前的学习中没有接触过“以曲代曲”的思想方法.因此，教师要首先帮助学生了解多项式函数的特点，才能帮助学生产生有效的化归.

在泰勒公式教学中，教师可以先给出一些具体的函数，如f1（x）=x4-2x3+4x2-3x+5，f2（x）=ln（2x+1），f3（x）=sin2x，通过计算这些函数在x分别取1，1.1，1.01时的函数值，使学生体会多项式函数在计算方面的优点.为了引导学生想到“以曲代曲”的方法，需要让学生再利用微分近似计算x=1.01时f2（x）=ln（2x+1）的值.使学生再一次体会“以直代曲”在近似计算中的作用.“以直代曲”本身就是一种化归的方法，这样就能进一步帮助学生引出“以曲代曲”，最终推导出泰勒公式.

2.3 反常积分教学

反常积分包括无穷区间上的反常积分（或无穷积分）和无界函数的反常积分（或瑕积分）.以无穷积

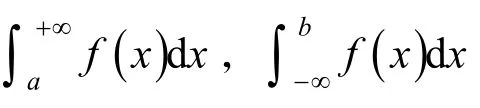
3　结语

化归在高等数学学习的很多方面还有体现，如重积分、曲线积分和曲面积分最终都是化为定积分来进行计算，求解二阶以及高阶常系数齐次线性方程的特征根法就是把微分方程的求解问题化为代数方程的求根问题等.由于高等数学知识点多，公式繁杂，学生常常感到难学.其原因往往在于学生只学会了记公式做题，而没有从化归的角度，从本质上理解知识之间的联系，导致每做一道题都感觉到是新题.因此，教师在教学时更要注意渗透化归思想，帮助学生找到新旧知识间的联系，培养学生掌握数学思想方法，提高他们的思维能力.应当注意到，学生对化归的掌握不是一次完成的，化归的方法也是多样的，教师在备课中要充分了解教材的整体安排与学生的认知特点，才能更好地促进教学，最终提高学生的学习效果.

参考文献：

［1］ 米山国藏.数学的精神、思想和方法［M］.成都：四川教育出版社，1986

［2］ 郑毓信.数学方法论入门［M］.杭州：浙江教育出版社，2006

［3］ 钱佩玲.数学思想方法与中学数学［M］.北京：北京师范大学出版社，2008

［4］ 张奠宙，过伯祥.数学方法论稿［M］.上海：上海教育出版社，1996

［5］ 姬利娜，郑群珍.化归思想在常微分方程教学中的应用［J］.河南教育学院学报：自然科学版，2012（3）：53-54

［6］ 徐兵.高等数学［M］.2版.北京：高等教育出版社，2010

［7］ 王尚志.普通高中数学课程分析与实施策略［M］.北京：北京师范大学出版社，2010

［8］ 杨小远，孙玉泉.泰勒公式与插值逼近的教学与实践［J］.高等数学研究，2012，15（4）：82-85

The application of reduction method in advanced mathematics teaching in independent colleges

LIU Wei
（Jingu College，Tianjin Normal University，Tianjin 300387，China）

Abstract：Advanced mathematics is a required course for science and engineering majors in independent colleges. However，the students in independent college have relative poor mathematical foundation.Discusses how to use the reduction method to improve the teaching of higher mathematics course in independent colleges from the perspective of reduction method.

Key words：reduction method；limit；Taylor's formula；improper integral；advanced mathematics

中图分类号：O13∶G642.0

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.019

文章编号：1007-9831（2016）05-0066-04

收稿日期：2016-01-01

基金项目：天津师范大学津沽学院教育教学研究课题（JKⅧ1407541）——数字媒体技术专业高等数学教学探索

作者简介：刘伟（1987-），男，河北唐山人，助教，硕士，从事数学学习论与数学课程论研究.E-mail：reaiyilin@163.com