若干数学竞赛试题的统一解法之注记

刘春平

(扬州大学数学科学学院，江苏扬州225002)



若干数学竞赛试题的统一解法之注记

刘春平

(扬州大学数学科学学院，江苏扬州225002)

[摘要]利用一个关于定积分的等式，给出了文献[1]中若干数学竞赛题的一种直接计算方法.

[关键词]数学竞赛； 定积分； 换元法

在文献[1]中，作者给出了一个关于积分的命题：

设f(x),g(x)为[a,b](b>a)上的连续函数.若

f(x)=f(a+b-x),g(x)+g(a+b-x)=m(常数)，

则有

(1)

然后用此命题对若干国内外数学竞赛试题进行了统一解答.这种将不同试题归类并提升到理论高度的文章[1,2]无论对教师的教学还是对学生的解题均有极好的启发作用.

在教学过程中，部分学生反映：命题中函数f(x),g(x)的选取并非一目了然，这在某种程度上影响了解题速度. 重新考察文献[1]中列举的竞赛题，我们发现这类定积分中被积函数具有某种“特殊性”，利用一个关于定积分的等式可直接计算. 下面，本文对此进行详细说明.

首先证明一个关于定积分的等式，它也是教科书上[3]的一道习题:

设f(x)为[a,b]上的连续函数，则

(2)

证令u=a+b-x,则

(3)

利用(2)式，对几道竞赛题重新解答如下.

试题(A)的解答.

由

试题(B)的解答.

由

知IB=1.

试题(C)的解答.

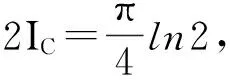
试题(D)的解答.

由

试题(E)的解答.

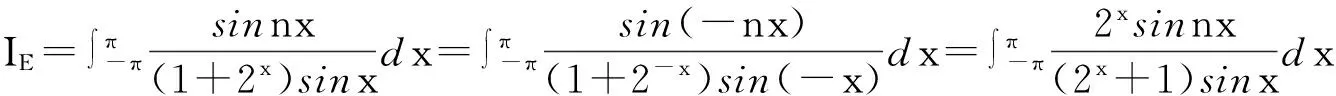
由

知n为偶数时,IE=0;n为奇数时，IE=π.

试题(F)的解答.

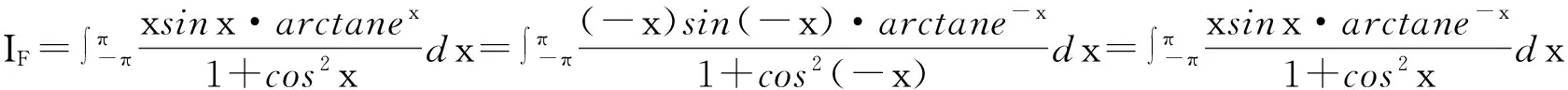
注意到

有

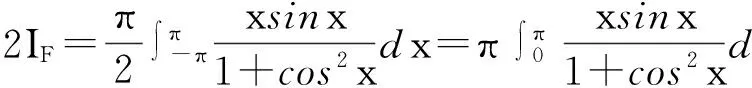
再由

得

解题思路便非常清晰了.

综上所述，当f(x)+f(a+b-x)为易积函数时，利用

[参考文献]

[1]潘杰，苏化明. 若干数学竞赛试题的统一解法[J]. 大学数学，2014，30(6)：111—114.

[2]苏化明，潘杰. 高等数学问题推广的几种方式[J]. 大学数学，2004，20(5)：64—69.

[3]同济大学数学系.高等数学上册[M]. 6版.北京: 高等教育出版社，2007: 253-254.

A Note on a Unified Solution to Several Mathematical Emulation Problems

LIUChun-ping

(Institute of Mathematics, Yangzhou University, Yangzhou Jiangsu 225002, China)

Abstract:By means of an equation on definite integral, one direct calculation method of several Mathematical Emulation problems recorded in literature [1] has been proposed.

Key words:mathematical emulation; definite integral； integration by substitution

[收稿日期]2016-01-17

[基金项目]江苏高校品牌专业建设工程资助项目(PPZY2015B109)

[作者简介]刘春平(1964-),女，博士，教授，从事微分方程研究.Email：liucp@yzu.edu.cn

[中图分类号]O172

[文献标识码]C

[文章编号]1672-1454(2016)02-0097-03