常系数非齐次线性微分方程特解的教学探讨

房庆祥，　张宝琳

(中国计量学院理学院，杭州310018)



常系数非齐次线性微分方程特解的教学探讨

房庆祥，张宝琳

(中国计量学院理学院，杭州310018)

[摘要]利用待定系数法和比较系数法求解一类高阶常系数非齐次线性常微分方程的特解，得到求解该类问题的一般公式，并给出算例说明其应用.

[关键词]线性常微分方程； 特解； 公式

1引言

求解常系数线性常微分方程是常微分方程和高等数学的重要内容，一般教材中介绍的方法主要有比较系数法、复数法、拉普拉斯变换法和常数变易法等[1-6].这些方法运算量较大，不利于手工求解.近年来，不少高校教师对求解常系数非齐次线性常微分方程的特解问题进行探讨，得到一些有益的结论.文献[7]将常系数线性微分方程转化为一阶常系数线性微分方程组，得到积分形式的特解公式.文献[8]对n阶常系数非齐次线性常微分方程的特解进行了探讨，得到不同形式的特解公式.文献[9]给出了求一类高阶非齐次线性微分方程(组)特解的矩阵解法.文献[10]提出一种求高阶常系数非齐次线性微分方程通解的逆特征算子分解方法.文献[11]研究一类具有多项式系数的二阶线性微分方程有多项式型特解和通解的充要条件，并给出判别和求解的Maple算法.上述文献中得到的结果拓宽了求解常系数非齐次线性微分方程特解的途径，为常微分方程教学提供了很好的素材，但公式表达形式不够简洁，不利于应用.文献[12]研究二阶常系数非齐次微分方程的求解方法，利用齐次方程的特征多项式表示特解，形式较简洁，易于记忆.本文把文献[12]的结论推广到n阶常系数非齐次微分方程的情形，得到求解高阶微分方程特解的一般公式.此公式形式简单，应用方便.

2高阶线性微分方程的特解公式

本文考虑如下常系数非齐次线性常微分方程特解的求解问题

(1)

其中f(t)=Aeαtcosβt或Aeαtsinβt，且a1,a2,…,an,A,α,β是实常数.

方程(1)对应的齐次微分方程的特征多项式为

F(λ)=λn+a1λn-1+…+an-1λ+an.

(2)

关于方程(1)的特解我们有如下结论.

定理1当f(t)=Aeαtcosβt时，如果α+iβ是F(λ)的k重根，则方程(1)的一个特解为

(3)

当f(t)=Aeαtsinβt时，如果α+iβ是F(λ)的k重根，则方程(1)的一个特解为

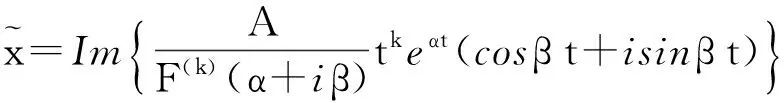
(4)

其中k≥0为整数.

证只证f(t)=Aeαtcosβt的情形，f(t)=Aeαtsinβt的情形类似.

易知，当f(t)=Aeαtcosβt时，微分方程

L[x]=Ae(α+iβ)t

(5)

的特解的实部是方程(1)的特解.

当k=0或1时，结论易证.

当k>1时，方程(5)的特解可设为

(6)

其中B为待定常数.

经简单计算可知, 当m≤k时

(7)

当m>k时，

(8)

+an-1Btk-1e(α+iβ)t(k+(α+iβ)t)+anBtke(α+iβ)t=Ae(α+iβ)t,

上式两边同除以e(α+iβ)t，然后比较多项式的系数可得

(9)

从而

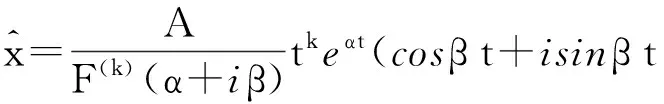
(10)

因此，表达式(3)是方程(1)的特解.

3微分方程特解公式的应用

本节举例说明定理1的应用.

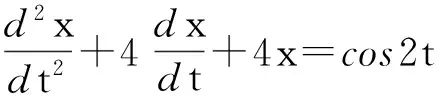
解因2i不是特征多项式

F(λ)=λ2+4λ+4=(λ+2)2

的根，根据定理1可得方程的一个特解为

注1例1是教材[1]中的例题.用定理1中的公式求解显然比用待定系法更简洁明了.

解因i是特征多项式

F(λ)=λ3+λ=λ(λ2+1)

的单根，根据定理1可得方程的一个特解为

解因i是特征多项式F(λ)=λ6+3λ4+3λ2+1=(λ2+1)3的3重根，根据定理1可得方程的一个特解为

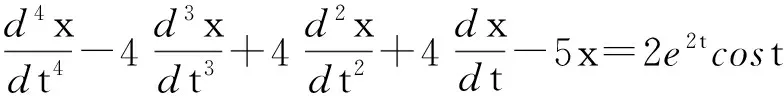
解因2+i是特征多项式

F(λ)=λ4-4λ3+4λ2+4λ-5=(λ+1)(λ-1)(λ-2-i)(λ-2+i)

的单根，根据定理1可得方程的一个特解为

解因1不是特征多项式

F(λ)=λ3+3λ2+3λ+1=(λ+1)3

的根，根据定理1可得方程的一个特解为

解分别考察方程

(11)

和

(12)

的解.

因-1+2i不是特征多项式

F(λ)=λ3+λ2-2=(λ-1)(λ+1-i)(λ+1+i)

的根，根据定理1可得方程(11)的一个特解为

因-1+i是特征多项式F(λ)=λ3+λ2-2的单根，根据定理1可得方程(12)的一个特解为

由叠加原理可得原方程的一个特解为

4结论

本文利用待定系数法和比较系数法得到求解一类高阶常系数非齐次线性常微分方程特解的一般公式，并举例说明公式的应用.本文得到的求解公式形式简洁，计算量较小，易于学生接受.

[参考文献]

[1]王高雄，周之铭，朱思铭，等.常微分方程[M].北京：高等教育出版社，2007.

[2]张伟年，杜正东，徐冰.常微分方程[M].北京：高等教育出版社，2006.

[3]丁同仁.常微分方程[M].北京：高等教育出版社，2010.

[4]焦宝聪.常微分方程[M].北京：清华大学出版社，2008.

[5]同济大学数学系.高等数学[M].北京：高等教育出版社，2006.

[6]庄万.常微分方程习题解[M].济南：山东科学技术出版社，2003.

[7]陈利娅，赖霞.常系数非齐次线性微分方程特解的另一种求法[J].高等数学研究，2010，13(4)：75-77.

[8]杨继明，苏亚丽，李周红.常系数非齐次线性微分方程的特解公式[J].数学的实践与认识，2011，41(7)：244-246.

[9]戴中林.求高阶非齐次微分方程(组)特解的矩阵解法[J].大学数学，2013，29(6)：125-129.

[10]郑华盛.高阶常系数非齐次线性微分方程的逆特征算子分解法[J].大学数学，2014，30(4)：76-81.

[11]胡亦郑，李素梅，罗勇.一类多项式系数二阶线性微分方程解法的研究[J].大学数学，2015，31(3)：27-33.

[12]张守贵.一类二阶常系数微分方程特解的教学探讨[J].重庆工商大学学报(自然科学版)，2012，29(12)：11-14.

Discussion on the Special Solution to a Class of Higher-order Ordinary Coefficient Differential Equations

FANGQing-xiang，ZHANGBao-lin

(School of Sciences, China Jiliang University, Hangzhou 310018, China)

Abstract:The special solution to a class of higher-order nonhomogeneous ordinary coefficient linear differential equations is investigated based on undetermined coefficient method and comparative coefficient way. The general formulas for solving this kind of problems are obtained. Some examples are given to show the practicability of the formulas.

Key words:higher-order ordinary differential equation; special solution; formula

[收稿日期]2015-12-07；[修改日期] 2016-03-04

[基金项目]中国计量学院教改项目(HEX2014019)，国家自然科学基金(11401549)

[作者简介]房庆祥(1974-)，男，硕士，副教授，主要从事复杂网络同步理论研究.Email:fangqx@cjlu.edu.cn

[中图分类号]O175.1

[文献标识码]C

[文章编号]1672-1454(2016)02-0102-04