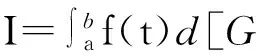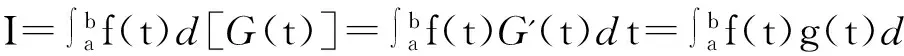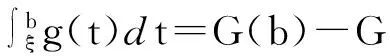Stieltjes积分在微积分教学中的应用

杜晓明

(华南理工大学数学学院， 广州510640)



Stieltjes积分在微积分教学中的应用

杜晓明

(华南理工大学数学学院， 广州510640)

[摘要]初学者在学习微积分时，容易对分部积分法、Abel判别法、Dirichlet判别法、积分第二中值定理等形式相近的内容产生混淆疑惑.Stieltjes积分能对这些内容作统一的处理，并给出十分直观的几何解释.

[关键词]Stieltjes积分； 分部积分； Abel判别法； Dirichlet判别法； 积分第二中值定理

1引言

2Stieltjes 积分

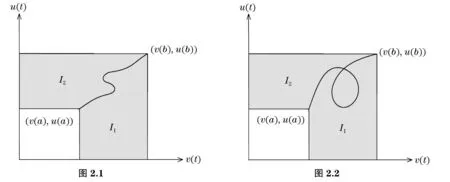
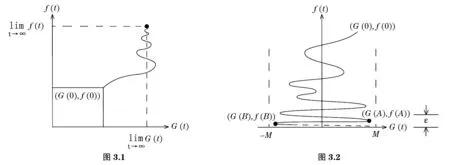
设f(t),G(t)为[a,b]上的函数.对于分划a=x0

若在max|xi-xi-1|→0时S的极限存在，且值为I，则它为 Stieltjes 积分, 可记为

若还有条件G(t)可导并且导数它的导数是g(t)，则以上积分还可改写成

几何意义：在一些特殊的情形之下，Stieltjes积分有明显的几何意义.当t在[a,b]之间变化时，坐标为(G(t),f(t))的点在坐标平面上给出一条曲线.

(a) 如果f(t)和G(t)都是连续单调递增的函数，则G(t)有反函数，曲线可以看作是f与G的反函数的复合函数的图像，I就是曲线下方与x轴所围住区域的面积(图1.1).

(b) 如果f(t)单调递增但G(t)不单调递增，则横坐标不再单调递增，曲线如图1.2.I同样是曲线右下方与x轴所围住区域的面积，只是这时纵坐标没法写成横坐标的函数.

(c) 如果f(t)和G(t)都不单调，则曲线可能发生自交，从而在中间形成一段闭曲线围住平面上某区域.这时曲线段围住区域的面积也要计入，正负号与曲线转圈的方向有关(图1.3，1.4).若围住区域的边界曲线是顺时针走一圈，则该部分的面积要重复计算，如图1.3，I=S1+2S2.若边界曲线是逆时针走一圈，则该部分的面积要被减去，如图1.4，I=S1-S2.

3分部积分法

几何意义：

记上面等式左方两项分别为I1，I2.则无论v(t)与u(t)是否单调，I1，I2均为Stieltjes型积分，分别对应着点(v(t),u(t))在t从a到b变化时画出的曲线右下方的面积和左上方的面积.这块面积等于两个矩形的面积之差(如图2.1).当曲线自交时，同样会在中间形成一段闭曲线围住平面上一块区域.这块区域的面积，在计算I1及I2时，在一边要重复计算，另一边要被减去(如图2.2).

于是两块面积的和I1+I2仍然为两个矩形面积之差.这两个矩形的面积分别为u(b)v(b)，u(a)v(a).

4广义积分收敛性的Abel判别法和Dirichlet判别法

几何意义：

5积分第二中值定理

g(t)在[a,b]上可积，f(t)在[a,b]上单调.则存在

ξ∈[a,b]，使得

几何意义：

[参考文献]

[1]菲尔金哥尔茨.微积分学教程(第三卷)[M]. 8版. 北京：高等教育出版社，2006:65-74.

The Application of Stieltjes Integral in the Teaching of Calculus

DUXiao-ming

(South China University of China, Guangzhou 510640, China)

Abstract:When learning calculus, many beginners confuse with the integration by parts, Abel's test, Dirichlet's test and the second mean value theorem for definite integrals. Stieltjes integral can handle these contents universally and give very intuitive graphical interpretations.

Key words:Stieltjes integral; integration by parts; Abel’s test; Dirichlet’s test; second mean value theorem

[收稿日期]2015-11-02；[修改日期] 2016-03-04

[基金项目]国家自然科学基金(11401219)

[作者简介]杜晓明(1980-),男，博士，讲师，从事低维拓扑研究.Email:scxmdu@scut.edu.cn

[中图分类号]O172.2

[文献标识码]C

[文章编号]1672-1454(2016)02-0114-04