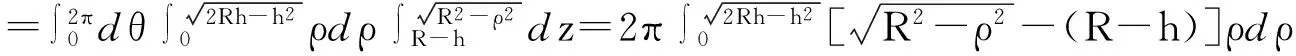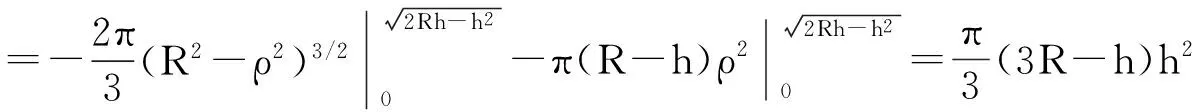球缺体积公式的多种证明

戴习民，　朱晓临，　张仁琼

(1.合肥工业大学数学学院,合肥230009；　2.合肥工业大学图书馆,合肥230009)



球缺体积公式的多种证明

戴习民1，朱晓临1，张仁琼2

(1.合肥工业大学数学学院,合肥230009；2.合肥工业大学图书馆,合肥230009)

[摘要]仅介绍球缺体积公式的七种证明方法，供大家在微积分的教与学中参考.

[关键词]球缺体积公式； 积分； 极坐标； 柱面积分； 球面积分； 极限

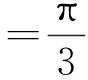
本文仅给出球缺的体积公式的多种证法，供大家在教学中参考.

证法一利用三重积分，采用“先二后一”法，本法是命题组给出的参考答案.

设球缺所在的球体表面的方程为x2+y2+z2=R2，球缺的中轴线为z轴，记球缺所在的区域为Ω，根据球缺的定义，0

证法二利用柱面坐标的三重积分，其球面方程同证法一，其体积为

本证法本质上与证法一是一致的.

证法六球面方程同上，其球面圆锥形区域为

利用球面坐标的三重积分得，球缺体积=球面底圆锥的体积-平底圆锥的体积，于是

证法七利用微元法求其体积，设球缺的高0

从而所求球缺体积

[参考文献]

[1]同济大学数学系.高等数学(上、下册)[M]. 6版.北京：高等教育出版社，2012.

A Variety of Proving Methods for the Hemispherical Segment Volume Formula

DAIXi-min1,ZHUXiao-lin1,ZHANGRen-qiong2

(1. Department of Mathematics, Hefei University of Technology, Hefei 230009,China;2. Library of HeFei University of Technology, Hefei 230009,China)

Abstract:Seven methods of proving the hemispherical segment volume formula are introduced in the paper,which offer reference in the teaching and learning of calculus.

Key words:hemispherical segment volume formula; integral;polar coordinates; column integral; spherical surface integral; limit

[收稿日期]2015-12-18

[基金项目]安徽省重点教研项目(2014jyxm),名师工作室(2015msgzs126),安徽省图工委重点项目(TGW14A02)

[作者简介]戴习民(1964-)，男，硕士，副教授，从事最优化理论和方法的应用研究.Email: daiximin@126.com

[中图分类号]O172

[文献标识码]C

[文章编号]1672-1454(2016)02-0100-02