有限交换环上常循环码研究

开晓山，　朱士信

(1.合肥工业大学 数学学院，合肥230009；　2.东南大学移动通信国家重点实验室，南京210096)



有限交换环上常循环码研究

开晓山1,2，朱士信1,2

(1.合肥工业大学 数学学院，合肥230009；2.东南大学移动通信国家重点实验室，南京210096)

[摘要]有限交换环上常循环码在代数编码理论研究中占有重要的地位，特别是在构造有限域上高纠错性能非线性码中有着重要的应用. 本文介绍了有限交换环上常循环码的研究进展，阐述了研究有限交换环上常循环码结构的一般方法及相关问题，分析了如何利用等距Gray映射构造有限域上的线性码.

[关键词]有限交换环； 纠错码； 常循环码； Gray映射； 生成多项式

1引言

纠错码理论产生于二十世纪四十年代后期, 经过七十多年的发展，有限域上纠错码理论逐渐走向成熟，经典的纠错码如Hamming码、BCH码与RS码等在实践中得到了广泛的应用，并且渗透到信息各个领域. 随着有限域上经典纠错码理论的深入发展，有限环上的纠错码也引起了人们的兴趣. 上世纪七十年代，众多学者对整数剩余类环m上线性码与循环码进行了研究[1-3]. 至上世纪九十年代，有限环上的纠错码研究获得了实质性突破，Nechaev[4]与Hammons等人[5]独立地证明了一些高效的二元非线性码可以看作是4上循环码的二元像，由此解决了二元非线性Preparate码与Kerdock码关于距离计数器具有形式对偶性这一困扰编码界二十多年的疑惑. 自此，有限环上纠错码理论研究成为代数编码理论研究的重要组成部分. 1997年，我国代数学家万哲先院士编写了有限环上纠错码理论专著《Quaternary Codes》[6]，标志着有限环上纠错码理论进入全面发展时期.

有限交换环上的常循环码是经典循环码的自然推广，由于这类码具有丰富的代数结构，自然地受到了学者的关注. Wolfmman在文献[7]中首次引入4上的负循环码，证明了4上线性负循环码的二元像是循环码，并且利用Gray映射得到了二元非线性优码. 此后，人们对有限交换环上的常循环码进行了广泛的研究(参见文献[8-16])，重点探讨各种有限交换环上的常循环码的结构. 本文主要介绍有限交换环上常循环码的研究状况及问题，我们将从有限交换链环与有限交换非链环两方面入手阐述其上常循环码的研究进展及研究方法.

2有限链环上的常循环码

性质2.1[17]设R是有限链环，其特征是pm(p是素数).设a是R的最大理想的生成元，幂零指数是t，则存在整数l与单位δ使得p=δal，其中1≤l≤t.

β=ξ0+aξ1+…+at-1ξt-1,ξi∈T.

任取(c0,c1,…,cn-1)∈Rn，对于给定R的一个单位λ，称变换

τλ(c0,c1,…,cn-1)=(λcn-1,c0,…,cn-2)

为Rn上的λ-常循环移位. 若R上长为n的线性码C在λ-常循环移位下不变，即

(c0,c1,…,cn-1)∈C，

得

(λcn-1,c0,…,cn-2)∈C，

这个多项式称为码字c的多项式表示. 本文中，视码字与其多项式表示为同一概念. 易见，在商环R[x]/〈xn-λ〉中，xc(x)对应于c(x)的一个λ-常循环移位. 由此得到下面结论：

性质2.2有限链环R上长为n的线性码C是λ-常循环码当且仅当C是商环R[x]/〈xn-λ〉的理想.

因此，研究R上长为n的λ-常循环码就转化为分析商环R[x]/〈xn-λ〉的结构，给出它的理想分类. 通常，随λ的选取不同，商环R[x]/〈xn-λ〉的结构也不同. 然而，当码长n与R的剩余域的特征p互素时，对不同的λ，商环R[x]/〈xn-λ〉的结构都相同. 文献[18]分类它的所有理想，并给出了它的每个理想的生成元. 下面，分两种情形讨论当n=ps时，商环R[x]/〈xn-λ〉的结构.

情形1λ=γ+ηa，其中γ∈T*，η是R的单位.

因为γ∈T*且T*是一个阶为pr-1的循环群，所以γpr=γ. 令ν=γpr-s，则νps=γ.

记R1=R[x]/〈xps-λ〉.设r(x)∈R1，显然r(x)可以惟一地表示成

r(x)=r0+r1(x-ν)+r2(x-ν)2+…+rps-1(x-ν)ps-1，

其中ri∈R, 0≤i≤ps-1.

引理2.3设

r(x)=r0+r1(x-ν)+r2(x-ν)2+…+rps-1(x-ν)ps-1∈R1，

证首先证明x-ν是R1中的幂零元. 在R1中，

注意到

无论p是奇素数还是偶素数，都存在多项式h(x)∈R[x]使得

(x-ν)ps=aη+ph(x).

由性质2.1得到

(x-ν)ps=a[η+δal-1h(x)]，

从而(x-ν)pst=0. 于是，x-ν是R1中的幂零元. 将r(x)可写成

其中r∈R,g(x)∈R1.

上式的常数项为

于是，h(x)可以表示为

其中bi∈R, 1≤i≤ps-1. 因此

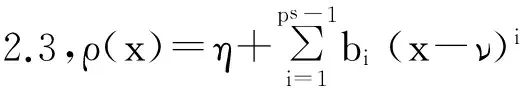
证设r(x)是R1中的任意元素，则r(x)可以表示成

r(x)=r0+ar1+(x-ν)g(x),

其中r0∈T,r1∈R,g(x)∈R1. 若r0=0，则

r(x)=ar1+(x-ν)g(x).

根据引理2.3，

a=(x-ν)psρ(x)-1，

其中ρ(x)是R1中的单位. 因此，存在h(x)∈R1使得

r(x)=(x-ν)h(x).

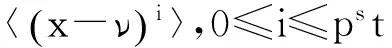
推论2.6设C是R上长为ps的η-常循环码，则

情形2λ=γ+ηaι，其中γ∈T*，η是R的单位，ι≥2.

记Rι=R[x]/〈xps-λ〉.设r(x)∈Rι，则r(x)可以惟一地表示成

r(x)=r0+r1(x-ν)+r2(x-ν)2+…+rps-1(x-ν)ps-1，

引理2.7在Rι中，当2≤ι≤l时，

其中β(x)是Rι中的单位. 因此，x-ν的幂零指数是psh，其中h=t/gcd(t,ι).

证类似于引理2.4的证明，容易得到

因为a的幂零指数是t，所以aι的幂零指数为h=t/gcd(t,ι). 注意到

是Rι中的可逆元， 因此x-ν是Rι中的幂零元，且幂零指数为h=t/gcd(t,ι).

定理2.8当2≤ι≤l时，环Rι是有限局部环，但不是有限链环，其最大理想是〈a,x-ν〉.

证设r(x)是Rι中的任意元素，则r(x)可以表示成

r(x)=r0+ar1+(x-ν)g(x),

a=(x-ν)f1(x)+[xps-(γ+ηaι)]f2(x).

取x=ν得到

a[1+ηaι-1f2(v)]=0，

从而a=0，矛盾，故a∉〈x-ν〉. 显然，x-ν∉〈a〉. 因此，〈a,x-ν〉不是主理想，这表明Rι不是有限链环.

当ι>l时，同样可以证明商环R[x]/〈xn-λ〉是局部环，但不是链环. 在这种情况下，通常不易确定R[x]/〈xn-λ〉中幂零元x-ν的幂零指数，因而很难对R[x]/〈xn-λ〉中的理想进行分类. 如何有效地给出R上长为ps的所有的λ-常循环码通常是一个很复杂的问题(参见文献[19-22])，利用离散的傅里叶变换可以将研究有限环R上任意长度N=psn(其中n与p互素)常循环码的结构问题转化为研究R的扩环上长为ps的常循环码(参见文献[10,16,23,24]). 因此，分类R上长为ps的λ-常循环码对研究有限环上常循环码具有重要的意义.

3有限非链环上的常循环码

随着有限链环上常循环码的研究深入，人们对一些有限非链环上的常循环码进行了探讨.Zhu等人在文献[25]中首先研究了四元非链环F2+vF2(其中v2=v)上循环码，给出了F2+vF2上循环码的性质与结构；随后，Zhu与Wang在文献[26]中研究了更一般的有限非链环Fp+vFp(其中v2=v)上(1-2v)-常循环码的结构，并利用等距映射得到Fp上最优码. 下面，我们介绍文献[26]如何利用Fp+vFp上常循环构造有限域上最优码.

有限环Fp+vFp(其中v2=v)是半局部环，它有两个最大理想〈v〉与〈1-v〉. 根据中国剩余定理

Fp+vFp=〈v〉⊕〈1-v〉.

因此，Fp+vFp上长为n的常循环码能分解两个线性码的直和，从而可以给出Fp+vFp上长为n的常循环码的结构，这是解决此类有限非链环上常循环码结构的一般方法. 下面进行具体说明. 设C是Fp+vFp上长为n的线性码，定义两个Fp上长为n的线性码如下：

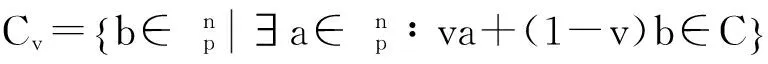
因此，线性码C可以表示为

C=vC1-v⊕(1-v)Cv.

若C=vC1-v⊕(1-v)Cv是Fp+vFp上长为n的(1-2v)-常循环码当且仅当C1-v与Cv分别为Fp上长为n的负循环码与循环码. 由此得到了Fp+vFp上长为n的(1-2v)-常循环码的结构.

定理3.1若C=vC1-v⊕(1-v)Cv是Fp+vFp上长为n的(1-2v)-常循环码，则

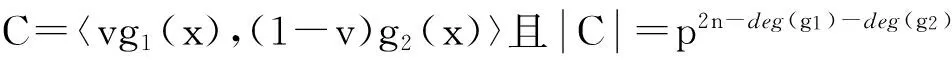
其中g1(x),g2(x)分别是C1-v与Cv的首一生成多项式.

φ：∀c=r+vq∈Fp+vFp，φ(c)=(-q,2r+q).

显然，映射φ可以拓展到(Fp+vFp)n上. 同时，定义Fp+vFp中元素的Gray重量如下：

定理3.2若C=vC1-v⊕(1-v)Cv是Fp+vFp上长为n的(1-2v)-常循环码，且

C=〈vg1(x),(1-v)g2(x)〉，

其中g1(x),g2(x)分别是C1-v与Cv的首一生成多项式，则φ(C)=〈g1(x)g2(x)〉.

定理3.2给出了Fp+vFp上长为n的(1-2v)-常循环码的Gray像，据此可以构造有限域Fp上线性码，文献[26]利用这个方法构造了三元[8,5,3]最优码. 该研究表明：利用某些有限非链环上的常循环码可以构造有限域上参数较好的线性码，因此有限非链环上纠错码的研究具有重要的意义. 随后，学者们对一些有限非链环上常循环码进行了研究(参见文献[27-29]). 这里，我们着重介绍文献[28]中利用有限非链环F2+uF2+vF2+uvF2上(1+u)-常循环码构造二元最优的线性码的研究情况. 为了方便，记

R=F2+uF2+vF2+uvF2，

其中u2=v2=0，uv=vu. 首先，注意有限环F2+uF2+vF2+uvF2是有限局部环，但不是链环，其惟一最大理想为

与环Fp+vFp不同，该环不能进行直和分解，因此上述分解方法不适于环R上常循环码的结构分析. 对于这类环上常循环码，目前常采用环同态的方法分析它们的结构. 下面进行具体说明. 记

Rn=R[x]/〈xn-(1+u)〉，Sn=(F2+uF2)[x]/〈xn-(1+u)〉.

考虑由R到F2+uF2的环同态

φ：∀e=a+ub+vc+uvd∈R，φ(e)=a+ub.

显然，φ可以拓展到Rn到Sn的环同态映射：

φ(c0+c1x+…+cn-1xn-1)=φ(c0)+φ(c1)x+…+φ(cn-1)xn-1.

设C是R上长为n的(1+u)-常循环码，定义两个F2+uF2上长为n的线性码如下：

将φ作用于码C，可以得到由C到Res(C)的环同态：φ(a+vb)=a，a,b∈Sn. 注意到Kerφ=Tor(C)且φ(C)=Res(C)，根据有限群第一同构定理，

利用上述环同态，文献[28]得到了码C的结构.

定理3.3设f(x)是x2n-1在F2[x]中的因子，h(x)=(x2n-1)/f(x). 若C是R上长为n=2km(其中m是奇数)的(1+u)-常循环码，则

C=〈f(x)+vp(x)+uvq(x),vg(x)〉，

(*)

其中在F2[x]中

且

deg(g(x))>deg(p(x))，deg(g(x))>deg(q(x)).

根据定理3.3中给出的码C的结构，利用码C的挠码与剩余码，在某种条件下就可以确定码C的Gray距离，从而构造长为4n的二元线性码.

定理3.4设C是R上长为n=2km(其中m是奇数)的(1+u)-常循环码，其形式如(*)式，若Res(C)与Tor(C)的Lee距离分别为d1,d2，且d1≥2d2，则C的Gray距离为2d2.

文献[28]利用上述方法构造了一些二元最优线性码，如[24,8,8]，[28,12,8]，[60,53,4]等. 由此可见，这类有限非连环上的常循环码也是构造二元最优线性码较好的码源. 因此，深入对该类环上纠错码的研究是十分必要的. 由于生成多项式惟一性不易判定，因此这类码的数目难以确定，因此R上形式不同的(1+u)-常循环码可能产生同一个二元线性码. 同时，完全确定每一个R上(1+u)-常循环码的Gray距离也是比较困难的. 这两个问题是目前研究这类有限非链环上常循环码遇到的主要困难，它的解决还需要进一步寻求新的方法.

4结论

本文主要从有限链环与有限非链环两方面介绍了有限交换环上常循环码的研究现状，具体阐述了研究有限交换环上常循环码结构的一般方法，分析了如何利用等距Gray映射构造有限域上的线性码. 有限交换环上常循环码是一类重要的线性码，它包含循环码与负循环码作为子类. 有限交换环上线性码可以构造各种序列，例如CDMA序列、调频序列与低相关性序列，还用于无线通讯的纠错编码方案. 因此，有限交换环上常循环码在理论与应用方面都具有广泛潜力. 最近，有限环上常循环码也被用于量子纠错码的构造(参见[30-32])，因此探讨有限交换环上常循环码的应用是一个重要的课题. 然而，分类有限交换环上任意长度的常循环码非常复杂，它是环上编码理论中非常具有挑战性的问题. 我们期待更多学者加入环上纠错码研究行列，共同推进该方向的应用与发展.

[参考文献]

[1]Blake I F. Codes over integer residue rings[J]. Information and Control, 1975, 29: 295-300.

[2]Spiegel E. Codes overm[J]. Information and Control, 1977, 35: 48-51.

[3]Shankar P. On BCH codes over arbitrary integer rings[J]. IEEE Trans. Inform.Theory, 1979, 25 (4): 480-483.

[4]Nechaev A A. Kerdock codes in cyclic form[J]. Dis. Math. Appl., 1991, 1 (4): 365-384.

[5]Hammons A R, Kumar P R, Calderbank A R, Sloane N J A, Sole P. The4-linearity of Kerdock, Preparata, Goethals, and related codes[J]. IEEE Trans. Inform. Theory, 1994, 40 (2): 301-319.

[6]Wan Z X. Quaternary codes[M]. Singapore：World Scientific, 1997.

[7]Wolfmann J. Negacyclic and cyclic codes over4[J]. IEEE Trans. Inform. Theory, 1999, 45 (7) : 2527-2532.

[8]Tapia-Recillas H, Vega G. A generalization of negacyclic codes[C]// In Proc. Int. Workshop on Coding and Cryptography, 2001: 519-529.

[9]Ling S, Blackford T.pk+1-Linear codes[J]. IEEE Trans. Inform. Theory, 2002, 48 (7) : 2592-2605.

[10]Blackford T. Negacyclic codes over4of even length[J]. IEEE Trans. Inform. Theory, 2003, 49 (6) : 1417-1424.

[11]Sǎlǎgean A. Repeated-root cyclic and negacyclic codes over finite chain rings[J]. Dis. Appl. Math., 2006, 154: 413-419.

[12]Dinh H Q. Complete distances of all negacyclic codes of length 2sover2a[J]. IEEE Trans. Inform. Theory, 2007, 53 (1): 4252-4262.

[13]Qian J F, Zhang L N, Zhu S X. (1+u)Constacyclic and cyclic codes overF2+uF2[J]. Appl. Math. Lett., 2006, 19: 820-823.

[14]Amarra M C V, Nemenzo F R. On (1-u)-cyclic codes overFpk+uFpk[J]. Appl. Math. Lett., 2008, 21: 1129-1133.

[15]Abualrub T, Siap I. Constayclic codes overF2+uF2[J]. J. Franklin. Inst., 2009, 346: 520-529.

[16]Kai X S, Zhu S X, Li P. (1+λu)-Constacyclic codes overFp[u]/[J]. J. Franklin. Inst., 2010, 347: 751-762.

[17]McDonald B R. Finite Rings with Identity[M]. New York: Dekker, 1974.

[18]Dinh H Q, López-permauth S R. Cyclic and negacyclic codes over finite chain rings[J]. IEEE Trans. Inform. Theory, 2004, 50 (8) : 1728-1744.

[19]Abualrub A, Oehmke R. On the generators of4cyclic codes of length 2e[J]. IEEE Trans. Inform. Theory, 2003, 49 (9): 2126-2133.

[20]Kiah H M, Leung K H, Ling S. Cyclic codes overGR(p2,m) of lengthpk[J]. Finite Fields Appl., 2008, 14: 834-846.

[21]Dinh H Q. Constacyclic codes of lengthpsoverFpm+uFpm[J]. J. Algebra, 2010, 324: 940-950.

[22]Sobhani R. Complete classification of (δ+αu2)-constacyclic codes of lengthpkoverFpm+uFpm+u2Fpm[J]. Finite Fields Appl., 2015, 34: 123-138.

[23]Dougherty S T, Ling S. Cyclic codes over4of even length[J]. Des. Codes Crypt., 2006, 39 (2): 127-153.

[24]Dougherty S T, Park Y H. On modular cyclic codes[J]. Finite Fields Appl., 2007, 13: 31-57.

[25]Zhu S X, Wang Y, Shi M J. Some results on cyclic codes overF2+vF2[J]. IEEE Trans. Inform. Theory, 2010, 56(4): 1680-1684.

[26]Zhu S X, Wang L Q. A family of constacyclic codes overFp+vFpand its Gray image[J]. Discrete Mathematics, 2011, 311: 2677-2682.

[27]Karadeniz S, Yildiz B. (1+v)-Constacyclic codes overF2+uF2+vF2+uvF2[J]. J. Franklin. Inst., 2011, 348: 2625-2631.

[28]Kai X S, Zhu S X, Wang L Q. A family of constacyclic codes overF2+uF2+vF2+uvF2[J]. J. Syst. Sci. Complexity, 2012, 25(5): 1032-1040.

[30]Kai X S, Zhu S X. Quaternary construction of quantum codes from cyclic codes overF4+uF4[J]. Int. J. Quantum Inform., 2011, 9(2): 689-700.

[31]Qian J F, Ma W P, Guo W M. Quantum codes from cyclic codes over finite ring[J]. Int. J. Quantum Inform., 2009, 7(6): 1277-1283.

[32]Ashraf M, Mohammad G. Construction of quantum codes from cyclic codes overFp+vFp[J]. Int. J. Inform. Coding Theory, 2015, 3(2): 137-144.

Research on Constacyclic Codes over Finite Commutative Rings

KAIXiao-shan1,2,ZHUShi-xin1,2

(1. School of Mathematics, Hefei University of Technology, Hefei 230009, China;2. National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract:Constacyclic codes over finite commutative rings play a significant role in algebraic coding theory, especially have important applications for constructing nonlinear codes over finite fields with high error-correcting performance. In this paper, we introduce recent progress of constacyclic codes over finite commutative rings, set forth general methods of studying constacyclic codes over finite commutative rings and related problems, and analyze how to construct linear codes over finite fields by using isometric Gray maps.

Key words:finite commutative ring; error-correcting code; constacyclic code; Gray map; generator polynomial

[收稿日期]2016-03-20

[基金项目]国家自然科学基金(61370089，61572168)；东南大学移动通信国家重点实验室开放研究基金(2014D04)

[作者简介]开晓山(1975-)，男，博士，副教授，从事代数编码理论研究.Email:kxs6@sina.com

[中图分类号]O157.4

[文献标识码]A

[文章编号]1672-1454(2016)02-0001-07