新正线性算子在Orlicz空间内逼近的强逆不等式
赵佳婧, 吴嘎日迪
(内蒙古师范大学数学科学学院, 呼和浩特010022)
新正线性算子在Orlicz空间内逼近的强逆不等式
赵佳婧,吴嘎日迪
(内蒙古师范大学数学科学学院, 呼和浩特010022)
[摘要]Agrawal和Thamer定义了一类新正线性算子,本文利用光滑模、Hardy-Littlewood极大函数、N函数的凸性及Jensen不等式,讨论了该算子在Orlicz空间内逼近的性质,给出并证明了该算子在Orlicz空间内逼近的强型逆定理.
[关键词]算子; Orlicz空间; 逼近; 强逆不等式
1引言和主要结果
关于算子逼近的问题,在连续空间和Lp空间中已有大量研究成果,Agrawal等[1]定义了一类新的正线性算子
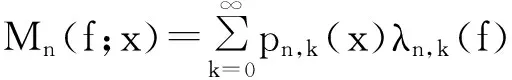
其中

约定pn,k(x)=0,k<0.权函数φ2(x)=x(1+x).李景斌[2]等研究了该算子在Lp空间内的逼近性质,文献[3]讨论了该算子在Orlicz空间内逼近的正逆定理,本文将在此基础上进一步研究该算子在Orlicz空间内逼近的强型逆定理.

的可测函数的全体{u(x)},由文献[4]知,上述Orlicz范数还可以由
文中C表示与n和x都无关的常数,不同位置取值不一定相同.
本文的主要结果如下:
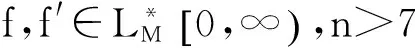

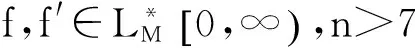

文献[5]定义了K-泛函和二阶光滑模


和一阶连续模

则有
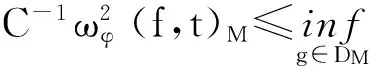

其中

P(D)g(x)=(φ2(x)g′(x))′.
2若干引理
引理1[6]对任意n∈N,k≥0,x∈[0,∞),有



证由Taylor展式

以及矩量估计式[1]有
Mn(f;x)-f(x)

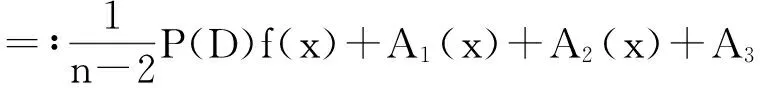
由文献[7]的引理1.1知

则有
‖A1‖M≤2n-1‖f′‖M,‖A2‖M≤24n-2‖φ2f″‖M,
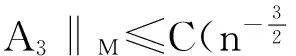
由此可以完成引理2的证明.

‖(Mnf)′‖M≤C‖f′‖M.
(1)
‖(Mnf)″‖M≤Cn‖f′‖M.
(2)
‖(Mnf)‴‖M≤Cn2‖f′‖M.
(3)
证这里只证(3)式,类似可得(1),(2)式.
记an(k)=λn,k(f), Δan(k)=an(k+1)-an(k), Δran(k)=Δ(Δr-1an(k)), r∈N.由文献[7]知
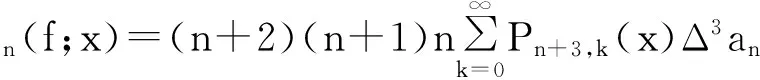
并且当k≥0时,有

经过计算可得
Δ3an(k)=an(k+3)-3an(k+2)+3an(k+1)-an(k)
=Δan(k+2)-2Δan(k+1)+Δan(k)

则有
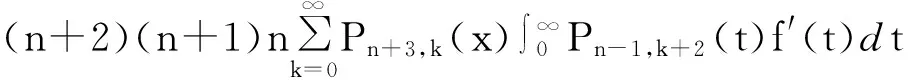


=∶‖I1‖M+2‖I2‖M+‖I3‖M.
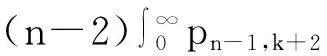

则有‖I1‖M≤Cn2‖f′‖M.同理可得‖I2‖M≤Cn2‖f′‖M,‖I3‖M≤Cn2‖f′‖M,(3)式得证.


证由文献[7]知

利用Hölder不等式知
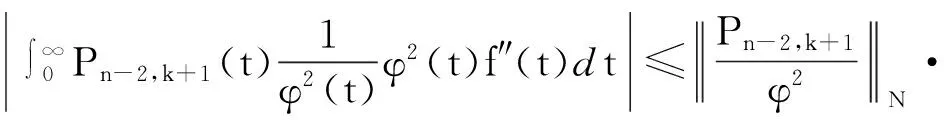
而



因此


可用类似于文献[7]中引理1.3的讨论方法得出

所以有


‖φ2g″‖M≤C(p)‖P(D)g‖M,
‖g′‖M≤C(p)‖P(D)g‖M.
证仿照文献[8]中引理5的证明过程,即可完成本引理的证明.
3定理的证明

(4)

(5)

(6)

(7)
利用引理2和引理5,结合(4)-(7)式得
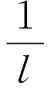




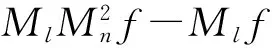
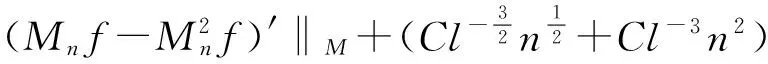
当l≥Ln时,由文献[6],以及文献[3]的引理3和引理5知
‖Mnf‖M≤C‖f‖M,‖φ2(Mnf)″‖M≤Cn‖f‖M,
则有
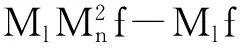

从而有

因此



定理2的证明由K-泛函和光滑模的等价性,结合引理5可得

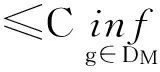
[参考文献]
[1]Agrawal P N,Thamer K J.Approximation of unbounded functions by a new sequence of linear position operators[J].Journal of Mathematical Analysis and Applications,1998,225(2):660-672.
[2]李景斌.一类新线性正算子的Steckin-Marchaund型不等式[J].兰州大学学报,2008,44(6):107-111.
[3]赵佳婧,吴嘎日迪.一类新线性正算子在Orlicz空间内的逼近[J].内蒙古师范大学学报,2016, 45(2):1-4.
[4]吴从炘,王廷辅.奥尔里奇空间及其应用[M].哈尔滨:黑龙江科学技术出版社,1983.
[5]Ditzian Z,Totik V.Moduli of Smoothness[M].New York:Springer-Verlag,1987.
[6]Heilmann M.Direct and converse results for operators of Baskakov-Durrmeyer type[J].Approx Theory& Its Appl,1989,5(1):105-127.
[7]刘国军,等.一类线性正算子Lp空间逼近的强逆不等式[J].四川师范大学学报,2014,37(6):814-819.
[8]丁春梅.Baskakov-Durrmeyer型算子的强逆不等式[J].信阳师范学院学报,1999,12(1):8-13.
[9]Ramazanov A R K.On approximation and rational functions in Orlicz spaces[J].Analysis Mathematica, 1984(10):117-132.
[10]Wu Garidi.On Approximation by Polynomials in Orlicz Spaces[J].Approximation Theory and its Applications,1991,7(3):97-110.
Approximation of New Positive Linear Operators Strong Converse Inequality in Orlicz Space
ZHAOJia-jing,WUGaridi
(College of Mathematics Science,Inner Mongolia Normal University,Huhhot 010022, China)
Abstract:Agrawal and Thamer gives a definition to a new class of positive linear operators. This dissertation discusses about the nature of its approach within the Orlicz Space on the basis of analyzing the following four concepts modulus of smoothness, Hardy-Littlewood great function,N-function and Jensen inequality,showing us proof of the approximation strong type inverse theorem.
Key words:operator;Orlicz space;approximation; strong converse inequality
[收稿日期]2015-11-24;[修改日期] 2016-03-25
[基金项目]国家自然科学基金(11161033);内蒙古师范大学人才工程基金(RCPY-2-2012-K-036)
[作者简介]赵佳婧(1990-),女,硕士研究生,从事函数逼近论方面的研究. Email:961604159@qq.com
[中图分类号]O174.41
[文献标识码]A
[文章编号]1672-1454(2016)02-0017-05

