一些特殊类型的变系数二阶线性微分方程解法的研究

文　武

(四川文理学院教务处，四川达州635000)



一些特殊类型的变系数二阶线性微分方程解法的研究

文武

(四川文理学院教务处，四川达州635000)

[摘要]运用变量变换的方法将一些特殊类型的变系数二阶线性微分方程化为常系数二阶线性微分方程，或已知齐次方程的一个解来求出齐次方程的另一个线性无关解，从而达到按照常系数二阶线性微分方程的特殊方法和利用常数变易法来求方程的通解的目的，同时纠正了文献[3]的结论和例子2的错误.

[关键词]变系数二阶线性微分方程； 特殊类型； 变量变换； 常数变易法； 通解

1引言

在大量的实际问题中，变系数二阶线性微分方程，一般说来都是不容易求解的.但是有些特殊类型的变系数二阶线性微分方程，则可以通过变量变换的方法将一些特殊类型的变系数二阶线性微分方程化为常系数二阶线性微分方程或者可求出另一个线性无关解的齐次线性方程.笔者认为不同的方程类型应该采取不同的方法来处理，有些特殊的方程可以采用专门的方法来求解就比较容易.在此，对一些特殊类型的变系数二阶线性微分方程解法的进行研究.

2研究结论

定义任何一个二阶线性微分方程

y″+P(x)y′+Q(x)y=f(x)，

(1)

总可以通过变换y=u(x)v(x)使原方程变为不含一阶导数项的方程

则称r(x)为常微分方程的不变式.

定理1变系数二阶线性微分方程y″+P(x)y′+Q(x)y=f(x)，经过线性变换y=u(x)v(x)可化为可解类型的方程

证作线性变换

y=u(x)v(x)，

(2)

这里u(x)，v(x)分别是待定和未知的函数(u是待定函数，v是未知函数)，作变换的目的是将函数y用函数v来代替). 为此，将(2)代入(1)，得

u(x)v″+[2u′(x)+P(x)u(x)]v′+[u″(x)+P(x)u′(x)+Q(x)u(x)]v=f(x)，

(3)

由此可见，方程(1)可经过线性齐次变换

(4)

化为关于v的不含一阶导数项的线性方程

(5)

因方程(1)在形如(4)的变换下，欲使方程(3)的对应齐次方程化为分离变量的可解类型方程，特别地，令v′的系数为0，即有2u′(x)+P(x)u(x)=0，得

将其代入(3)整理，得

(6)

从而函数r(x)的确定形式不会改变，即r(x)为方程(1)的不变式，且r(x)为可积函数时，方程(1)可经变换(4)化为可解类型的方程.

推论1当

为常数时，方程方(1)可化为常系数二阶线性微分方程.

推论3当

定理2变系数二阶线性微分方程y″+P(x)y′+Q(x)y=f(x)，经过线性变换

可化为常系数二阶线性微分方程

的充分条件是P(x)-Q(x)≡k1，且

其中k1，k2为常数.

证明过程类似于定理1，从略.

的充分条件是Q′(x)+2P(x)Q(x)=0.

将它们代入方程(1)得

当且仅当Q′(x)+2P(x)Q(x)=0时，就有

即结论得证.

定理4[3]变系数二阶线性齐次方程方y″+P(x)y′+Q(x)y=f(x)，经过变量变换

y=e∫F(x)dxu(x)，t=∫G(x)dx，

可化为常系数二阶线性微分方程的充分条件是P(x)，Q(x)满足下面方程组所给出的形式，

(7)

其中f(x)，F(x)，G(x)都是x的已知连续函数，且G(x)可微，G(x)≠0，k为实常数.

证作变量变换

y=e∫F(x)dxu(x)，t=∫G(x)dx，

(8)

将函数y换成u，并将自变量x换成t，则有

(10)

(11)

通过变换t=∫G(x)dx可以求出x是t的函数，从而方程(11)的右端也是t的函数，于是可以求出方程(11)的解u(t)，把t换成∫G(x)dx，变得u(x)，从而方程(7)的解为

注通过对本文定理4的推导，指出了文献 [3]中推导的结论

应该是

(12)

利用定理2作变换

(13)

将(13)代入(12)得二阶常系数线性方程

(14)

注(14)式右端将t=∫G(x)dx代入转化为t的函数.

由定理2的特别情况下可知二阶Euler方程

x2y″+a1xy′+a2y=f(x)

注运用定理2来求出方程(1)的解，问题的关键在于如何找到函数F(x)，G(x)及实常数k.在通常情况下，先把一般的方程变成标准的方程(1)的形式，然后通过观察比较、凑微分、分项组合相结合满足(7)的要求.一般而言，先确定常数k和G(x)，从而就可以确定出F(x)并加以验证.

定理5设y1为变系数二阶线性齐次方程方y″+P(x)y′+Q(x)y=0的一个非零解，则它的另一个线性无关解为

从而它的通解为

这里c1，c2为任意常数.

证令y=y1u，则

y′=y′1u+y1u′，y″=y″1u+2y′1u′+y1u″

代入y″+P(x)y′+Q(x)y=0，得

y1u″+[2y′1+P(x)y1]u′+[y″1+P(x)y′1+Q(x)y1]u=0，

即y1u″+[2y′1+p(x)y1]u′=0，引入新的未知函数z=u′，方程变形为

是一阶线性方程，解之得

则

这里c1，c2为任意常数.取

y1与y2之比不等于常数，故y1，y2线性无关，因而原方程的通解为

这里c1，c2为任意常数.

亦可这样证明：令

则有y1y′-y′1y=e-∫P(x)dx,从而有

即有

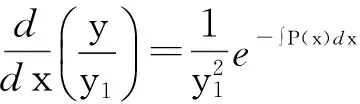
故

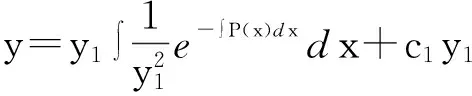
于是可取

显然y1与y2线性无关，因而原方程的通解为

这里c1，c2为任意常数.

3举例

故令

将原方程化为常系数方程：v″+v=0，得上式通解为

v=c1cosx+c2sinx，

这里c1，c2为任意常数.故原方程的通解为

这里c1，c2为任意常数.

例2解方程x2y″-xy′+y=x.

解方程变形为

(15)

(16)

这里c1，c2为任意常数.故原方程的通解为

这里c1，c2为任意常数.

解原方程变形为

(17)

令

(18)

于是由(11)得原方程化为二阶常系数方程

即

u=c1e-t+c2et，

这里c1，c2为任意常数.

非齐次方程

有一个特解u*=-2t，从而方程

的通解为

u=c1e-t+c2et-2t

故原方程的通解为

这里c1，c2为任意常数.

注文献 [3]中的例2求方程

的通解. 文献 [3]求出的通解为

而此解不是原方程的通解，应该是本文例3 方程

的通解.

例4求方程xy″-xy′+y=0的通解.

解方程有特解y1(x)=x，原方程变形为

故原方程的通解为

这里c1，c2为任意常数.

4结束语

一般的变系数二阶线性微分方程是是不容易求解的，除了常微分方程教材中介绍了极少的特殊方程的求解方法外，本文又给出一些特殊类型的变系数二阶线性微分方程的解法，尤其是介绍了二阶Euler方程的另一种解法，掌握这些类型的解法还是有重要实际意义的.

[参考文献]

[1]王高雄,等. 常微分方程[M].北京：高等教育出版社，1978.

[2]东北师范大学数学系微分方程教研室.常微分方程[M].北京：高等教育出版社，1982.

[3]张学元.变系数二阶线性常微分方程的一个新的可解类型[J]. 大学数学，2003，19(1)：96-98.

[4]李高，常秀芳.关于二阶变系数线性常微分方程求解法的研究[J]. 大学数学，2010，26(6)：12-14.

Some Methods for Solving Second Order Linear Differential Equations with Variable Coefficients

WENWu

(Teaching Affairs Office of Sichuan University of Arts and Science, Dazhou Sichuan 635000, China)

Abstract:The variable transformation method , which is used for solving some special types of the second order linear differential equations with variable coefficients, and for calculating the another linearly independent solution through a known solution for the second order linear differential equations with constant coefficients，is discussed in this paper . Also, for the second order linear differential equations with constant coefficients, the method in this paper associated with variation of constants formula can be used for finding the general solution. In addition, some mistakes in literature [3] are corrected.

Key words:the variable coefficient; the second order linear differential equation; variable transformation； variation of constants formula； general solution

[收稿日期]2014-11-16；[修改日期] 2016-03-11

[基金项目]四川省高等学校人文社会科学重点研究基地项目 (NYJ20150604)

[作者简介]文武 (1967-)，男，硕士，副教授，从事运筹学与控制论. Email:104078213@qq.com

[中图分类号]O175.1

[文献标识码]C

[文章编号]1672-1454(2016)02-0106-08