超环面电机蜗杆内定子感应电动势的分析计算*

刘　欣，　王云洋，　黄　凯

(天津工业大学 天津市现代机电装备技术重点实验室，天津　300387)



超环面电机蜗杆内定子感应电动势的分析计算*

刘欣，王云洋，黄凯

(天津工业大学 天津市现代机电装备技术重点实验室，天津300387)

摘要：介绍了超环面电机及其驱动原理。建立了超环面电机行星轮磁齿运动的轨迹方程，并讨论了电机参数对行星轮磁齿运动轨迹的影响。推导出行星轮磁齿的运动在蜗杆内定子绕组内产生电动势的计算公式。对该公式进行分析和计算，总结了各个参数对电动势的影响规律。对超环面电机内定子绕组电动势波形进行了测试试验，试验结果与计算结果规律基本吻合，验证了理论分析的正确性。

关键词：超环面电机； 电动势； 蜗杆内定子； 行星轮磁齿

0引言

航空航天和工业控制等领域对电力的需求越来越大，各类电动机的应用越来越广泛，也对电机提出了性能良好、单位重量轻和体积小等要求。因此，需要在电机的新原理、新结构和新的运行方式方面不断进行研究和探索。

随着各种科学的相互渗透与交叉发展，电机与各种传动结构集成的研究受到广泛关注[1-3]。该集成特点是简化了电力驱动系统的结构，将动力驱动与传动特色集于一体，能克服机械传动中的摩擦损耗和振动噪声等，且具有效率更高、可控性更强、过载自我保护等优点[4-6]。超环面电机是集传统行星蜗杆传动、电磁驱动技术和控制技术于一体的新型空间电机。由于在结构上其具有两个环面，即蜗杆内定子上一个外环面和环面外定子上一个内环面，故称之为超环面。该电机除了具有普通磁性齿轮优点外，因其结构功能的集成特点，输出转矩转速可控，响应速度快等，在航空航天和车辆等领域具有广阔的应用前景[7-8]。

1超环面电机的结构原理

图1为超环面电机的结构示意图，主要由蜗杆内定子、行星轮、环面外定子和行星架转子组成。蜗杆内定子铁心是由硅钢片叠压组成，表面均匀分布有空间螺旋的电枢槽，槽内安放有电枢绕组，用以形成旋转磁场；行星轮圆周上安装有若干个永磁体，形成行星轮的永磁齿；环面外定子是由若干个NS极空间相间的螺旋永磁梁组成，为超环面电机提供固定的磁场；行星架转子是由一定数目的行星轮固联在一起而组成。当蜗杆内定子绕组通入三相交流电后，在其外表面空间产生螺旋的旋转磁场，行星轮磁齿在该旋转磁场和环面外定子永磁梁作用下受到磁场力的作用，该磁场力在行星轮圆周切线方向上的分力使行星轮产生自转，沿行星轮轴向方向上的分力使行星轮发生公转，行星轮的公转带动行星架转子转动，从而实现超环面电机转矩的输出。

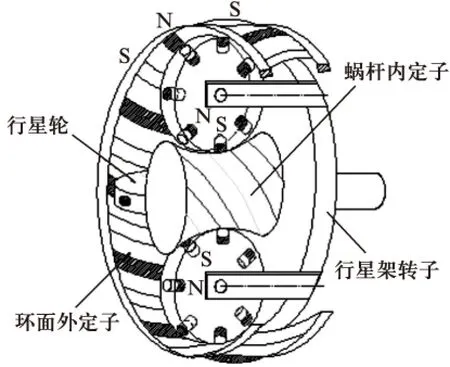
图1　结构示意图

在超环面电机运行过程中，行星轮在内外定子之间公转的同时也在自转，其上磁齿则在内外定子间做环状的螺旋运动。这种特殊的运动，行星轮磁齿运动在内定子电枢绕组产生的感应电动势与普通电机的分析与计算相比有其特殊性。该电动势又会对该种电机的气隙磁场产生影响，从而影响该电机的输出转矩。因此，需要对行星轮磁齿运动轨迹进行分析。

2行星轮磁齿运动

2.1行星轮磁齿轨迹方程

为分析蜗杆内定子和行星轮磁齿之间的电磁啮合，以蜗杆内定子的几何中心为坐标原点，蜗杆轴为z轴建立内定子坐标系O-XYZ，如图2所示。任意磁齿A的运动轨迹方程为：

(1)

图2　内定子坐标系

图2中，a为蜗杆内定子与行星轮间的中心距；R为行星轮半径；α为磁齿绕Z轴转过的角度；β为磁齿所在截圆在内定子包角范围内的位置角。其中φv为蜗杆内定子包角，实际取π/2。由于该电机的传动关系可知行星轮磁齿轨迹为绕着蜗杆内定子公转且随着行星轮中心架自转，公转一周和自转的圈数成一定的比例：

(2)

式中：k——比例系数；

Z0——环面外定子齿数；

Z2——行星轮磁齿数。

2.2参数对运动轨迹影响

若蜗杆内定子极对数为p，行星轮与内定子磁极间电磁啮合的同时，为了保证行星轮磁齿与环面外定子永磁梁的充分啮合，环面外定子齿数必须在2p的基础上成对增加NS极。由此可得环面外定子齿数需要满足：

Z0=2p(1+2n)

(3)

式中：n——自然数。

由以上算式分析可得Z0、Z2和p参数对行星轮磁齿运动轨迹影响规律如图3所示。

图3　结构参数对行星轮磁齿运动规律的影响

从图3可知，随着外环面定子齿数Z0的增多，行星轮磁齿运动旋转的圈数增多；随着行星轮磁齿数Z2的增多，行星轮磁齿运动旋转的圈数减少。当a增大时，行星轮磁齿运动的圆半径变大；当R改变时行星轮磁齿所在行星轮轨迹圆半径改变。从图3中也可以得出行星轮磁齿的运动与自身磁齿及环面定子齿数有关，则行星轮磁齿运动圈数为

q=Z0/Z2

(4)

3蜗杆定子电路分析

超环面电机蜗杆内定子绕组接上三相电源电压(相电压为u1)时，则有三相电流通过(相电流i1)。该电流产生的旋转磁场会在内定子相绕组中产生感应电动势e1，行星轮磁齿的运动也会在内定子绕组中产生动生电动势。图4所示为某一行星轮磁齿的空间运动轨迹与内定子绕组间的空间关系。为了便于分析，现将此空间感应产生的动生电动势分为两部分： 行星轮磁齿竖直方向运动分量产生的e2和磁齿水平方向运动分量产生的的e2′。蜗杆内定子每相绕组上的电压平衡方程式为

u1=i1R1+(-e1)+(-e2)+(-e2′)

(5)

图4　行星轮磁齿运动与内定子绕组的空间关系

3.1螺旋磁场产生的感应电动势

三相电源所产生旋转磁场切割内定子绕组得到的感应电动势

(6)

式中：Bm1——旋转磁场产生气隙基波磁密的幅值；

l1——旋转磁场切割内定子绕组的有效长度；

v1——线速度，v1=2πτf1，f1为交流电频率；

τ——超环面电机内定子的极距。

分析得l1的有效长度为蜗杆内定子绕组的螺旋长度，则

l1= ∫π/4-π/4x·2(β)+y·2(β)+z·2(β)=

(7)

3.2行星轮公转蜗杆绕组产生的电动势

行星轮磁齿竖直方向运动内定子绕组间的空间关系如图5所示。行星轮公转使得磁齿切割竖直方向绕组，根据法拉第电磁感应定律，蜗杆内定子回路中产生感生电动势。

图5　行星轮磁齿运动与绕组竖直方向空间关系

行星轮单磁齿对单相绕线竖直方向的感应电动势为

(8)

式中：Bm2=Bmsin(ω1t)，Bm为行星轮公转产生气隙基波的磁密的幅值，而某一行星轮磁齿在磁场运动中忽近忽远，类似绕着圆运动的正弦曲线如图5所示。ω2′=Z0/Z2·ω2为行星轮自转的角速度；ω2=2πf2为公转的角速度，f2为行星轮公转频率；v2=w2/p·R=2πf2/p·R=2πf2R/p为磁齿的线速度；l2=2Rsin(φv/2)为导体竖直方向的有效长度。

由算式得周期T为Z2/Z0f和1/f的公倍数。代入ω2=2πf2，ω2′=3.5ω2，f2=10Hz可以计算出公式的周期为0.1s；式(8)中磁密B、有效长度l2增大，则电动势增加，且随着磁齿的线速度增加电动势也增加。

3.3行星轮自转蜗杆绕组产生的电动势

行星轮磁齿运动轨迹在水平方向内定子绕组间的空间关系如图6所示。行星轮自转使得磁齿上下运动，从而切割绕组竖直方向和导线长度方向，根据法拉第电磁感应定律，蜗杆内定子回路中产生感生电动势。

图6　行星轮磁齿运动与绕组水平方向空间关系

行星轮单磁齿对单相绕组水平方向的感应电势为：

(9)

式中：Bm2′=Bmcos(ω1t)，水平方向动生电动势的产生与磁场水平方向有关；l2′=2πr为导体水平方向的有效长度；r为内定子的平均直径，此时为磁齿在蜗杆喉部的直径。

由算式得周期T为Z2/Z3f和1/f的公倍数。代入ω2=2πf2，ω2′=3.5·ω2，f=10Hz可以计算出算式的周期为0.1s。

3.4仿真结果

以上分析是建立在某一磁齿对蜗杆绕组所产生感应电动势，而实际中是多个磁齿共同运动所得。因此计算行星轮磁齿运动过程中产生的电动势时需要对多个电动势进行叠加，计算得

e=e1+e2+e2′=Bm1l1ν1sin(ω1t)+

(10)

根据式(10)，取计算电动势的主要参数如表1所示。

仿真计算出对绕组产生的电动势之和如图7所示。

表1　超环面电机蜗杆绕组感应电动势主要参数

图7　多磁齿产生的电动势

由上述所得周期为0.1s，而图7中可知实际输出小于这个周期，原因为超环面电机的水平方向半径并非一致，在喉部部分半径最小而在两头部分半径最大所，导致周期并非严格一致。图7中产生有两个一样凸起和凹陷部分，分析为磁感线切割竖直方向分量时，竖直方向分量是不变的，只是磁通在变化；而磁感线切割水平方向分量时，半径从喉部到两边是对称所导致的。

4试验验证

根据以上所述，研制了一台超环面电机试验样机，并搭建了测量蜗杆绕组中感应电动势波形图平台，如图8所示。图8中，原动机为交流电机，可以通过调频调速测量不同速度下的波形图；中间为试验样机；示波器为显示测量电动势波形。

图8　试验平台

观察测量行星轮的转动情况，当调频器显示电机转速为956r/min时，示波器显示的波形图如图9所示。

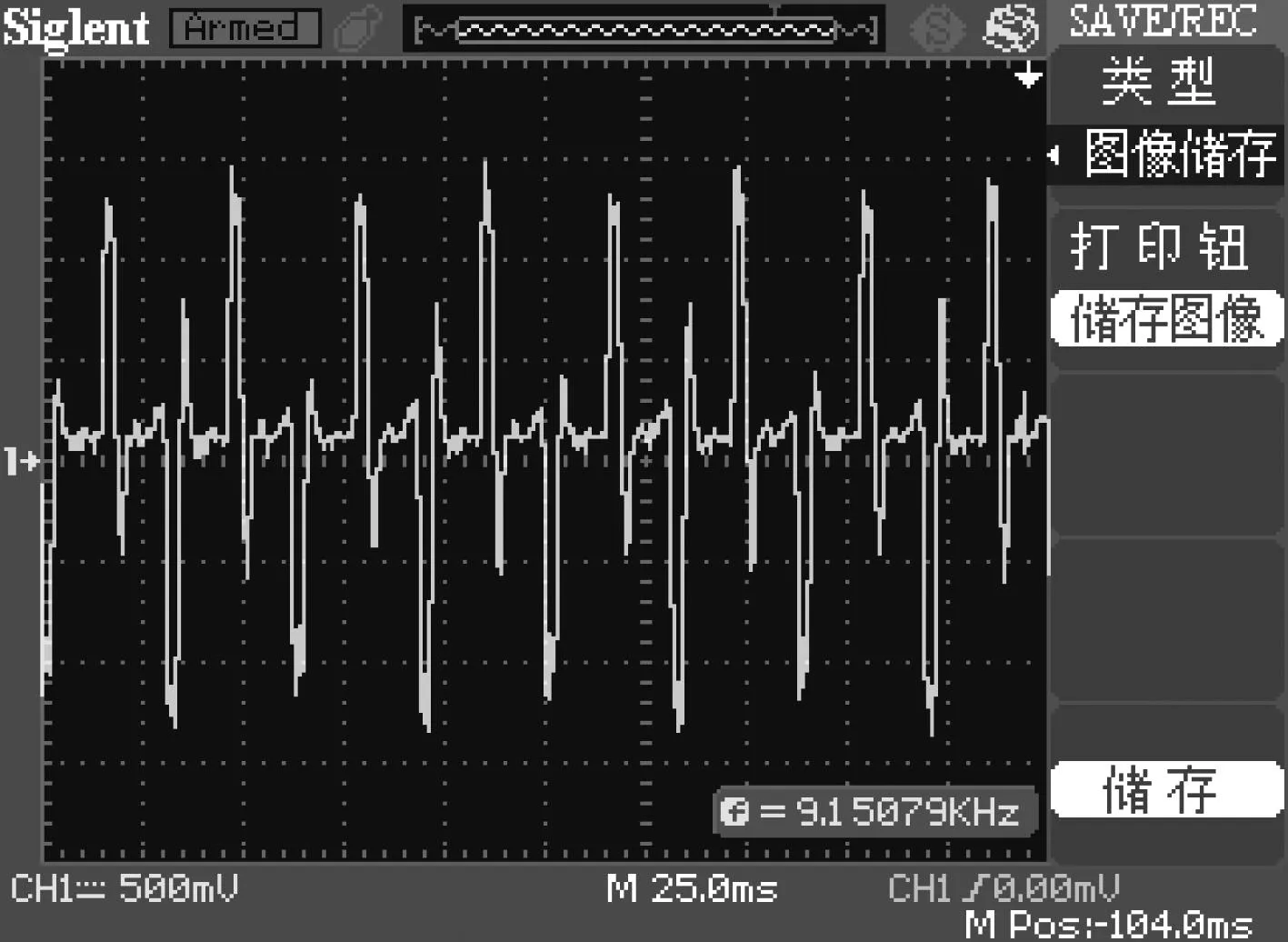
图9　试验测波形图

仿真验证时对公转进行模拟，行星轮公转过程中蜗杆环面包角同时只能满足三个磁齿对蜗杆绕组进行切割，而实际测得波形图也是三个磁齿对蜗杆绕组感应的电动势，因此产生的感应电动势为

(11)

则根据式(11)可得对蜗杆绕组产生电动势如图10所示。

图10　行星轮三个磁齿所产生电动势

对比图10和图9可知，蜗杆电枢绕组产生感应电动势与实际波形存在一定的偏差。这是由于蜗杆感应电动势与两条主磁路有关，而行星轮磁齿与环面外定子磁齿和蜗杆内定子之间的啮合磁路有关。理论值方面主要考虑行星轮磁齿与蜗杆内定子啮合磁路，并未计算环面外定子与行星轮磁齿啮合磁路的影响，并且试验样机存在一定制造精度和装配精度的误差。

5结语

超环面电机是一种新型集成空间电机。通过介绍该电机结构以及行星轮磁齿运动轨迹的分析，推导出行星轮磁齿运动轨迹方程，得到在不同参数下轨迹形状。在分析行星轮磁齿运动轨迹的基础上，对其在内定子绕组内产生的电动势进行推导，并对该电动势进行仿真计算。通过测试试验验证了其理论计算的有效性，为进一步研究该电机的性能提供依据。

【参 考 文 献】

[1]李争，王咏涛，葛荣亮，等.永磁球形多自由度电机研究进展综述[J].微电机，2011，44(9)： 68-70.

[2]柴凤，崔淑梅，宋立伟，等.双定子永磁同步电动机的结构设计[J].微电机，1999，32(6)： 12-24.

[3]朱孝勇，程明，华为，等.新型混合励磁双凸极永磁电机磁场调节特性分析及实验研究[J].中国电机工程学报，2008，28(3)： 90-95.

[4]WANG L L， CHAU K T. A coaxial magnetic gear with halbach permanent-magnet arrays[J]. IEEE Transactions on Energy Conversion， 2010，25(2)： 319-328.

[5]赵朝会，秦海鸿，严仰光.混合励磁同步电机发展现状及应用前景[J].电机与控制学报，2006，10(2)： 113-117.

[6]张卓然，耿伟伟，戴冀，等.新型混合励磁电机技术研究与发展[J].南京航空航天大学学报，2014，46(1)： 24-26.

[7]唐任远.现代永磁电机理论与设计[M].北京： 机械工业出版社，1997.

[8]冯垚径.永磁同步电动机设计关键技术与方法研究[D].武汉： 华中科技大学，2012.

欢迎投稿欢迎订阅欢迎刊登广告

网上投稿：motor-abc.chinaelc.cn

Analysis and Calculation of Induction Electromotive Force in the Inner Stator of the Toroidal Motor*

LIUXin，WANGYunyang，HUANGKai

(Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology，Tianjin Polytechnic University， Tianjin 300387， China)

Abstract：A toroidal motor with dual-stator and its driving principle were presented. Establishing in the center of the worm for axis of planetary magnetic tooth movement trajectory equation， the influence of motor parameters on the trajectory was discussed. The star wheel tooth movement deduce magnetic formula to generate electromotive force of stator winding in the worm. The influence of various parameters on the electric potential is analyzed and calculated. Finally， the toroidal stator winding EMF waveform test， experimental results and the rules are basically consistent， to verify the correctness of the theoretical analysis.

Key words：toroidal motor； electromotive force； the worm inner stator； planetary wheel magnetic gear

收稿日期：2014-09-21

中图分类号：TM 301

文献标志码：A

文章编号：1673-6540(2016)04- 0040- 05

作者简介：刘欣(1981—)，女，博士研究生，讲师，研究方向为超环面电机特性分析与控制研究。王云洋(1991—)，男，硕士研究生，研究方向为超环面电机电磁特性分析。

*基金项目：国家自然科学基金项目(51207107)；大学生创新创业训练计划项目(201410058125)