一种基于Elman回归神经网络检测谐波方法*

马立新，　张海兵，　项　庆，　周　磊

(上海理工大学 光电信息与计算机工程学院，上海　200093)



一种基于Elman回归神经网络检测谐波方法*

马立新，张海兵，项庆，周磊

(上海理工大学 光电信息与计算机工程学院，上海200093)

摘要：提出了基于Elman回归神经网络提取检测谐波电流的方案。通过MATLAB/Simulink仿真试验结果，验证了算法的可行性。该算法不仅能够满足检测谐波实时性的要求，同时在检测谐波的精度上有较大提高。

关键词：检测谐波； Elman回归神经网络； MATLAB/Simulink

0引言

随着电力电子器件在工业控制中的大量应用，谐波电流与无功功率对电能质量的污染问题也日益严重。传统的LC滤波器通过滤除特定次谐波的方法已经不能满足现代工业对电能质量的苛刻要求，有源电力滤波器(Active Power Filter, APF)是一种能够动态消除谐波并且可以补偿无功的电力电子设备，其应用从根本上解决了电力系统中动态滤波和无功补偿的问题[1]。与无源滤波器相比，APF具有高度可控性和快速响应性，不仅有实现同时对谐波与无功功率进行补偿的功能，并且不会与电网发生谐振，没有过载现象等优点，是目前最为理想的滤波设备[2]。

目前实际中使用的APF中检测谐波的方法，都是基于传统的ip-iq瞬时无功理论的谐波电流检测方法。然而，该算法在设计中使用到低通滤波器，由低通滤波器的传递函数可知，系统只有经过采集一定数量的点后才能进行滤波计算，因此，基于瞬时无功理论检测谐波电流的方法设计上就存在一定的误差[3]。基于此，寻找到更优的检测谐波电流的方法开始愈发得到相关研究人员的关注。人工神经网络的发展给谐波检测提供了新的途径，常见的是应用BP神经网络，通过将神经网络理论与自适应噪声对消技术相结合的方法来滤除谐波[4]。本文是在此基础上提出了一种基于Elman回归神经网络和锁相环(Phase Locked Loop， PLL)相结合的方法来滤除谐波电流分量，并利用MATLAB/Simulink搭建仿真模型，通过验证试验说明该算法的可行性，仿真试验结果也进一步表明了该算法与传统的无功理论检测谐波电流的方法相比较，前者滤波检测精度高、实时性强。

1APF工作原理

图1为APF的拓扑结构图。由于主电路中通过并联大电容来稳定直流侧电压，所以称之为并联型有源滤波器。当电网接入非线性负载工作时，通过电流传感器检测出补偿对象负载电流iL中的谐波电流iLh，利用指令电流运算电路将其反极性后即作为指令电流信号iC*。根据指令电流信号iC*，补偿电流发生电路产生实际的补偿电流信号iC，即与负载侧的谐波电流分量iLh大小相等、方向相反。由于两者相互抵消，所以补偿后的电源电流iS中只含有基波电流。其中补偿电流发生电路是由电流跟踪控制电路、驱动电路以及主电路三个部分共同组成的。

图1　并联型APF的拓扑结构图

2谐波检测思想

在电网正常工作时，电网电流应该为标准的50Hz正弦基波。其表达式如式(1)所示。

i(t)=Imsin(100πt+θ)

(1)

式中：Im——基波的幅值；

θ——初相角。

由式(1)可知，当确定了基波电流的幅值和初相角后，基波电流就可以确定了[5]。图2为Elman神经网络检测谐波原理图。当接有非线性负载时，采样三相电网电流ia(t)、ib(t)、ic(t)，通过PLL对其进行锁相，即可得到幅值为1、初相角与电网电流一致的单位正弦电流ifa1(t)、ifb1(t)、ifc1(t)；再利用Elman神经网络计算得到三相基波电流幅值Ifa、Ifb、Ifc。将单位正弦电流与其相对应的基波电流幅值相乘即可得到三相基波电流ifa(t)、ifb(t)、ifc(t)，再以电网电流减去基波电流，即得到需要滤除的谐波电流iLha(t)、iLhb(t)、iLhc(t)[6]。

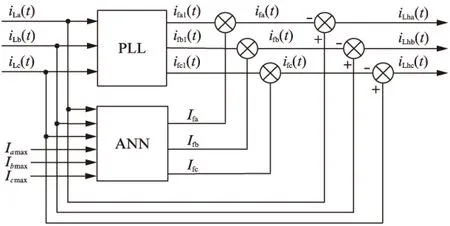
图2　Elman神经网络检测谐波原理图

以A相为例，基波电流ifa(t)的算式为

ifa(t)=ifa1(t)×Ifa

(2)

则有，谐波电流iLha(t)的算式为

iLha(t)=iLa(t)-ifa(t)

(3)

3Elman神经网络构造

本文叙述的滤波方法，是一种反馈型神经网络来计算得到基波幅值，总共有3层网络结构[7]。图3所示为Elman回归神经网络幅值检测结构图。第1层为输入层，依次输入6项采样值，包括畸变的三相电网电流ia(t)、ib(t)、ic(t)，以及同一周期内的电流采样最大值Iam(t)、Ibm(t)、Icm(t)。第2层为隐含层，由于Elman神经网络隐含层运用神经元个数越多，相对的精度也会提高，但网络的复杂程度也会成倍的增加，神经网络的训练时间也就更长[8]，因此结合实际情况本文所用的网络中隐含层包含30个神经元。第3层为输出层，即为工频基波电流的幅值Iaf1(t)、Ibf1(t)、Icf1(t)。

图3　Elman回归神经网络幅值检测结构图

神经网络的隐含层传递函数选择tansig函数(双曲正切函数)：

f1=2/(1+e-2s)-1

(4)

输出层传递函数选择purelin函数(线性函数)：

f2=s

(5)

分别得到隐含层输出：

X1(i)= [b1(i)+∑6α=1w1i(α)X0(α)+

(6)

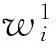
网络输出：

(7)

将三相电网电流当前值，以及前一个周期内的三相电流最大值作为该神经网络的输入样本值，训练函数采用学习率可变的动量BP算法来进行网络的离线训练。文献[9]中给出BP神经网络与锁相环相结合的方法来检测谐波电流。本文通过将采样值分别输入到两个训练网络中，通过训练仿真比较得出仿真结果，进一步说明本文叙述的算法的优越性。

4Simulink系统仿真与结果分析

根据以上分析，利用MATLAB/Simulink软件进行仿真。

仿真系统的基本参数为： 系统电网电压U=220V，整流桥选用触发角为0°的二极管整流电路，负载侧参数为R=100Ω，L=2mH，C=100μF。设置仿真时间为0.15s，在系统运行之前首先要通过三相负载电流以及电流峰值训练得到Elman神经网络模块。

由于三相电网的对称性，仿真结果以A相电流波形来说明。参考文献[9]中提出的基于BP神经网络滤波方法我们得到： 其中图4(a)是滤波前A相电网电流谐波频谱图，不妨取仿真的第一个周期时间段；图4(b)是滤波后A相电网电流谐波频谱图，并取以0.1s开始的下一个周期。可得知系统在0.04s处并入电网开始工作，比较两者可以很清楚地看到该方法的滤波效果较为明显，谐波滤除后总谐波失真率(Total Harmonic Distortion, THD)为4.37%，但是仍然可以看到滤波后的电流波形有不规则曲线。

图4　滤波前后A相电网电流谐波频谱图

图5是在其他条件都相同的情况下，基于Elman神经网络结合锁相环滤波后的A相电网电流谐波频谱图。同样我们取0.1s时刻后的一个周期，从系统仿真结果中可以看出，当系统运行至0.05s时，补偿后的A相电网电流开始趋于稳定[10]。相对于BP神经网络，Elman神经网络补偿电流可以实时跟踪谐波电流，补偿后的THD为2.76%，滤波效果更加明显。

图5　基于Elman神经网络滤波后谐波频谱图

5结语

本文提出了基于Elman反馈型神经网络和锁相环相结合来提取谐波电流的方法。在离线训练神经网络的条件下，通过与BP前向型神经网络训练相比较，容易看出Elman神经网络的目标输出更加容易计算得出，网络训练收敛速度更快。

对APF整个系统搭建MATLAB/Simulink仿真模型，仿真结果说明该控制策略能够较好地实现谐波提取，满足谐波监测的实时性和准确性的要求。

【参 考 文 献】

[1]崔景秀,孙志宏.基于用户侧谐波和无功补偿的谐波检测法研究[J].江西电力，2008，32(3)： 1-4.

[2]李圣清，彭玉楼，周有庆.一种改进型自适应谐波电流检测方法的研究[J].高电压技术，2002，28(12)： 3-4.

[3]徐洋.电网谐波抑制技术及提高电能质量的方法研究[J].电源技术应用,2013(1)： 35-36.

[4]都洪基,苏炜宏,邓烽.一种基于神经网络的谐波电流抑制方法[J].南京理工大学学报,2003，27(1)： 28-32.

[5]周波.一种无锁相环的单相电路谐波和无功电流检测方法[J].四川电力技术,2009,32(3)： 41-43,60.

[6]杨杰,赖声礼,李心广,等.三相电压不对称时谐波与基波有功、无功电流的精确检测方法研究[J].继电器,2003,31(4)： 6-9.

[7]PECHARANIN N, MITSUI H, SONE M. Harmonic detection by using neural network[J]. Proceedings of IEEE International Conference, 1995,27(2)： 923-926.

[8]邸斌,简优宗.负载电流检测型有源滤波器新的控制策略[J].电机与控制学报，2013，17(9)： 99-104.

[9]马立新,肖川,林家隽,等.神经网络与锁相环相结合的谐波检测方法[J].电力系统及其自动化学报,2011,23(3)： 24-29.

[10]冯亚琼,王昕,周荔丹,等.神经网络自适应PI控制器在有源滤波器中的应用[J].电力系统保护与控制,2011,39(16)： 74-79.

A Harmonic Detection Method Based on Elman Neural Network*

MALixin,ZHANGHaibing,XIANGQing,ZHOULei

(College of Optical-Electrical and Computer Engineering, University of Shanghai for Science &Technology, Shanghai 200093, China)

Abstract：The scheme to extract the harmonic current based on Elman recurrent neural network was presents, illustrating the feasibility of the algorithm through the MATLAB/Simulink simulation experiments.The algorithm can not only meet the requirements of real-time of harmonic detection， but also has great improvement in the accuracy of the harmonic detection.

Key words：harmonic detection; elman recurrent neural network; MATLAB/Simulink

收稿日期：2015-08-17

中图分类号：TM 306

文献标志码：B

文章编号：1673-6540(2016)04- 0086- 04

作者简介：马立新(1960—)，男，博士，教授，研究方向为电力系统稳定性与优化运行、电力电子与电力传动、电气系统故障诊断与模式识别。

*基金项目：上海市张江国家自主创新重点项目(201310-PI-B2-008)；沪江基金(C14002)