浅谈一题多解在高等数学中的应用——以分段函数定积分解法为例

段 燕

（临汾职业技术学院 山西临汾 041000）



浅谈一题多解在高等数学中的应用
——以分段函数定积分解法为例

段 燕

（临汾职业技术学院 山西临汾 041000）

摘 要：一题多解的情况在数学中很常见，初等数学中的简单函数问题常遇到一题多解，在高等数学中也有很多应用。本文以分段函数定积分的解法为例，浅谈一题多解在高等数学中的应用。通过不同的解题方法，提高发散性思维能力，增强创新意识，丰富数学知识。

关键词：一题多解 高等数学 分段函数定积分

引言

定积分包括积分第一、第二中值定理、拉格朗日中值定理、柯西中值定理、牛顿—莱布尼茨定理和泰勒定理。分段函数定积分在解题过程中需要合理运用这些定理，可以用不同的方法解题。本文将举例分析分段函数定积分的一题多解，进而浅析一题多解在高等数学中的应用。［1］

一、定积分的定理

1.积分中值定理

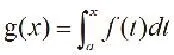
2.拉格朗日中值定理

拉格朗日中值定理也叫拉氏定理，它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形，是泰勒公式的弱形式（一阶展开）。［2］

如果函数f（x）满足：

（1）在闭区间［a，b］上连续；

（2）在开区间（a，b）内可导；

那么在开区间（a，b）内至少有一点x（a＜x＜b）使等式F（b）-f （a）=f’（x）（b-a）成立。

3.柯西中值定理

柯西中值定理为拉格朗日中值定理的推广，也是微积分的基本定理之一。其几何意义为，用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦。

设函数f（x），g（x）满足

（2）在开区间（a，b）内可导；

（3）对任意x∈false（a，b），g’（x）≠0，

4.牛顿—莱布尼茨定理

牛顿—莱布尼茨定理揭示了定积分与被积函数的原函数或者不定积分之间的联系。其内容是一个连续函数在区间 ［ a，b ］ 上的定积分等于它的任意一个原函数在区间［ a，b ］上的增量。［3］

如果函数f（x）在区间［a，b］上连续，并且存在原函数F（x），则：

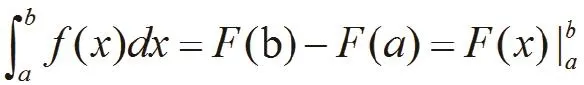
5.泰勒定理

泰勒公式用于函数在某点的信息描述其附近取值，如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

泰勒公式可以用（无限或者有限）若干项连加式（-级数）来表示一个函数，这些相加的项由函数在某一点（或者加上在临近的一个点的n+1 次导数）的导数求得。对于正整数n，若函数

二、分析一题多解在高等数学中的意义

1.提高发散性思维能力

现在中国很注重培养人们的思维能力，不再是古代传统的死记硬背。一题多解能帮助人们提高发散性思维，不同的解法从用不同的方式解决同一个问题，就像万千条道路都通向同一个目的地。高等数学不仅仅是教给人们数学公式，更重要的是培养人们利用数学知识去解决问题，培养数学思维能力。一题多解就是数学中锻炼人们发散性思维的方式之一。将数学中的发散性思维用于生活更是其乐无穷。

2.提升高等数学的兴趣

除了对数学特别感兴趣的人以外，普通人面对一大推的公式符号，还是会感到枯燥无味的。一题多解可以激发人们探索的兴趣，引发人们去思考。人都是由好奇心的，同一道题可以有不同的方式去解，解题的过程是对数学知识的一种巩固，也是对数学世界的探索过程。当问题解决之后，解题人也会有成就感。

3.提高创新意识

一题多解需要有创新意识，不满足于固定的解题模式，探索新的解题方法。做一道题，需要学会举一反三，不仅要熟知已学的知识，还要做到温故而知新。任何领域都需要创新才能进步，创新是发展的源泉。在数学中，一题多解正是培养创新意识的好方式。

三、总结

一题多解在高等数学中很常见，本文只是以分段函数定积分为例，简单分析了一题多解。分段函数的知识在生活中也很容易遇到，在不同的取值区间，函数表达式不同，分段函数定积分的解题方式很具有代表性。在高等数学中有一题多解，其他领域也一样，给我们的启示就是遇到问题不要局限于一种思维模式，要尝试不同的方法。

参考文献：

［1］郎丽丽，张喜红，康育慧，等.浅谈一题多解在高等数学教学中的应用——以分段函数定积分解法为例［J］.数理医药学杂志，2015-04-15.

［2］李伟勋； 李中.关于新编《高等数学》教材增设“一题多解”的探讨［J］.科教文汇（中旬刊），2015-10-20.

［3］张秀蓉.高等数学视角下的中学数学教学研究——以函数教学为例［D］.福建师范大学，2014-06-01.