基于学习力视角的高中数学课程建设

唐恒钧，陈碧芬，张维忠

(浙江师范大学教师教育学院，浙江金华　321004)



基于学习力视角的高中数学课程建设

唐恒钧，陈碧芬，张维忠

(浙江师范大学教师教育学院，浙江金华321004)

[摘要]育人多样化、办学特色化是国内外高中教育改革的普遍趋势。学科课程建设是实现上述改革目标的关键。以数学学科为例，以学科学习力发展为基础，分析了学科本质、学生发展需求，并提出了高中数学课程的分层分类体系，即根据课程功能分为补差、基础、拓展与研究等四个层次的课程；根据学生发展现状，将补差层课程分为知识与经验类、思维与方法类、兴趣与价值类课程；根据学生发展倾向，将拓展层与研究层分为服务于有数学兴趣与研究志趣的学生和服务于数学兴趣不大与研究志趣不明显的学生等两大类课程。

[关键词]数学学习力；数学本质；数学发展需求；数学课程建设

《国家中长期教育改革和发展规划纲要( 2010-2020年)》(以下简称《纲要》)提出，要推动普通高中多样化发展，推进培养模式多样化，满足不同潜质学生的发展需要。浙江省于2012年启动的深化普通高中课程改革，正是在该思想指导下的一次探索。高中学校特色化、学生个性化发展成为浙江省本轮课程改革的核心主题词。事实上，如英国[1]、日本[2]等国家的高中教育改革也普遍体现了育人多样化、办学特色化的趋势。

就学校而言，选修课程与必修课程是一个整体中的两个基本组成部分，两者之间既有课程形态、课程功能上的区分，同时又是相互协调的。特别是，选修课程的设置与实施并非随意的，是基于学生发展需求和学校办学定位与育人理念的，同时也是与相关必修课程融为一体的。因此，在学校课程建设的过程中，一个重要的问题便是如何构建学科课程体系？这在我国的高中实践中是一个新问题，理论上探讨也不多。本文尝试以数学学习力培养为指向，从学科、教育两个视角理解学校课程建设的基础，并提出学校数学课程建设的基本思路。

一、数学学习力：数学课程建设的基本指向

吴也显、刁培萼认为，学习力是现代人基础性的文化素质，具有学习力的人就是善于学习，智慧学习的人。[3]这在信息社会这一时代背景下显得更为重要。这个时代要求人成为终身学习者，掌握无定式的复杂思维方式和工作方式。裴娣娜将学习力理解为学生的生长力，并将其视为未来社会人才的基本素养。

学习力的内涵要比学习能力丰富。郭黎岩等认为，中小学生学习力包括学习动力、学习毅力、学习能力、学习转化力、学习创造力五个要素[4]。裴娣娜提出了学习力三层次六要素结构模型：第一层次的知识与经验、策略与反思、意志与进取；第二层次的实践与活动、协作与交往；第三层次的批判与创新。本文所讨论的学习力是在这一总的结构模型基础上，结合数学学科的特点而提出的。数学学习力应包括“知识与经验”、“思维与方法”、“兴趣与价值感”三个基础要素，“欣赏与理解”、“实践与体悟”、“合作与交流”三条基本途径，以及作为高级层次的“批判与创新”。

其中，“知识与经验”包括数学的基础知识与基本活动经验；“思维与方法”是指学生具有用数学思考问题的习惯，并拥有相应的方法与能力；“兴趣与价值”是指学生对数学学习和用数学思考问题的兴趣，但兴趣并不必然能持久，而价值是使学生保持持久动力的重要因素。

图1　数学学习力结构

“欣赏与理解”、“实践与体悟”、“合作与交流”是数学学习力发展的三条重要途径。数学学习需要让学生有冷静思考与充分表达的时间与空间。“欣赏与理解”、“实践与体悟”强调学生的冷静思考，强调对外在对象的内化，强调思维的内部运作；而合作与交流则同时强调倾听与表达，强调思维的外化和显性化。其实这三个过程也是相互促进的。具体而言，欣赏与理解、实践与体悟中的思维是内隐的，有时还是混沌的，而思维在外化的过程(即交流)中得到清晰化，同时合作与交流的过程又能引发新的更为丰富的观点与思考，进而为欣赏与理解、实践与体悟提供新的内容。反过来，如果没有欣赏与理解、实践与体悟，数学中的合作与交流就可能会流于形式，至少会流于表面。换言之，欣赏与理解、实践与体悟为深层次的数学合作与交流提供了基础。

“批判与创新”是学习力结构中的最高层次，是理想的追求，但这并不意味着是学习力的终极结果。首先，学习力的各组成要素是作为一个整体存在于学习者之中，而并非单纯地追求该结构中的高级层次。其次，学习力在发展过程中，也并非是由处于基础层的三个要素向“批判与创新”的单向发展，批判与创新也能反过来促进基础层次的三个要素发展。比如，正是具有批判与创新精神的人，才会在面对一个问题时不断地探索新的解决办法，并比较、评价不同方法间的优劣。后者即会促进学习者学习与积累更多的思维方式与方法。换言之，学习力结构中的四大要素、三大途径之间是相互作用、互促互进的，但对不同的学习者而言，学习力发展的“触发点”并不相同。比如，对于我国许多重点高中的学生而言，数学知识与经验是较为扎实而丰富的，也会有比较强的价值感(尽管这些价值感也许来自考试、升学等外在价值，而非来自学科内在的兴趣与价值感)，但在思维与方法、批判与创新等方面相对薄弱，因此要提升这些学生的学习力，一个较好的策略在于从思维与方法这一维度入手，强调数学问题解决的思想方法。相反，上述策略对于一些数学较为薄弱的学校而言注定不会理想，因为这超出了学生的现实水平，而且这些学生首先要解决的数学学习问题恐怕还是兴趣问题，而不是思维与方法问题，因此这类学校要从兴趣与价值这一角度入手。再次，如图1中的虚线锥体所示，学习力作为一个整体又是不断发展的，原来的学习力是新学习力发展的基础。

在学校数学课程建设中，不仅课程体系的建构需要考虑学生的学习力结构，更重要的是在每一门课程的建设中综合考虑学习力各要素，以促进学生数学学习力的发展。

二、学科本质与学生需求：数学课程建设基础

(一)数学的学科本质

任何一个学科的课程建设都必然要讨论学科的本质。就数学学科而言，即是需要讨论“什么是数学”这一基本问题。它将保证所建设的数学课程具有数学特质。正如张奠宙所指出的，数学教育，自然是以“数学内容”为核心[5]，在遵循一般教育规律的基础上，就需要对数学内容有深刻的认识，善于揭示数学实质，那种“去数学化”的倾向是不可取的[6]。反之，也正是由于对数学本质的认识偏差导致严重的负面影响。比如，中央电视台曾经为了配合2002年国际数学家大会在中国召开，在制作数学传播节目时进行了一项的公众问答调查，结果显示数学在大多数公众的心目中是一堆数字和公式，是抽象、深奥的符号，对于公众来说甚至是“神秘”的代言词。而2013年新浪网发起的关于“数学是否应该滚出高考”的讨论中，支持者的理由中大有将“数学”等同于“计算”、甚至“算钱”等实用技能。这些调查都表明公众对数学本质认识的偏面性，而这种认识偏差在很大程度上源于学校数学课程与教学中过于强调了如数学形式化、数学计算等某些方面，而忽视了另外一些方面。

关于“什么是数学”，数学家、数学哲学家等有诸多论述。数学哲学家Ernest( 1991)把数学观笼统地分成了三类，即问题解决的观点、柏拉图主义的观点和工具主义的观点[7]。一些研究表明，中小学数学教师、学生主要持柏拉图主义数学观[8][9]，将数学看作为一个通过逻辑将知识联系在一起的、静态的、永恒不变的学科。而出现上述现象的一个可能的重要原因就在于学校的数学课程所传递的信息：数学知识内容的抽象性；数学知识组织的逻辑性；数学知识叙述的片断性[10]。克莱因在其名著《古今数学思想》的序言中就明确地指出：通常一些课程所介绍的是一些似乎没有什么关系的数学片断；它们给出一个系统的逻辑叙述，并且这些课程完全经过锤炼，已成定局；学生被湮没在成串的定理中。[11]

因此，在高中数学课程建设的过程中，要全面地认识数学的本质。特别是把握以下三个方面。第一，数学从其内容与发展历程看存在明显的两重性，即数学内容的形式性与数学发现的经验性。波利亚曾指出，“数学有两个侧面，一方面它是欧几里得式的严谨科学，从这个方面看，数学是一门系统的演绎科学；另一方面，创造过程中的数学，却像是一门试验性的归纳科学。”[12]然而，在过去的高中课程中，过于强调了数学作为演绎科学的一面，而忽视了另一面。这一点在21世纪初的课程改革中已有所强调，但后者在必修课程的教材编制中会因时间、内容容量、学校层次差异等诸多因素所限而无法充分体现。这就需要在必修课程校本化、选修课程的建设中加以补充。第二，要真正在课程中体现数学发现的经验性这一特征，其前提是承认数学是一门动态发展的科学(这也就是Ernest所说的问题解决的观点)，即认识到数学是由问题驱动的，一门有待探索的、不断发展的学科，而不是僵化的封闭的规则体系。第三，也正是在数学的两重性之下，数学的基本要素除了逻辑、分析与一般性外，还包括直觉、构造与个别性。前三个基本要素主要体现了数学理论的抽象性、严谨性和形式化的特点，后三个则体现了数学发现过程中的直观性、经验性和归纳性特征。

(二)高中学生的数学发展需求

学生的发展需求是学校课程设置与实施的出发点与归宿。因此，无论是必修课程的校本化实施，还是选修课程的设置与实施都需要细致地分析学生需求。值得进一步说明的是，这里的学生发展需求不仅仅是学生自身所认识到的需求，也包括社会对人才规格的要求。正如《纲要》所指出的，高中阶段教育是学生个性形成、自主发展的关键时期。因此，学生的需求既有共性，又有个性；既有作为公民所应具备的共性素养的共同需求，又有作为未来职业规划后的个性素养的独特需求。就数学学科的角度而言，主要包括以下方面的需求。

首先，是进一步学习的需求。高中学生经过九年的学校学习，在数学上形成了不同的基础，而要有效地学习，并达成高中三年数学学习之后的共同基础，就需要通过必修课程的校本化和选修课程的设置，以满足学生进一步学习数学的补差需求和发展需求。

其次，作为未来数学创造者的需求。对于数学上有天赋，未来可能从事数学研究的学生，除了对学科前沿的了解外，更重要的在于数学学习与研究的方法论渗透。

再次，作为数学消费者的需求。其实未来会真正从事数学研究的学生的比例是相当小的，而更多的人则会以数学消费者的身份出现。这里的数学消费者是指，在未来的职业生涯或生活中会有意无意地用到数学知识和数学思想，但不直接创造数学。这类学生所需求的数学也许不像前一类学生那么前沿与精深，但更强调数学意识、数学思维习惯和方法。当然，数学消费者对数学的要求也有层次之分。以有美术兴趣的学生为例，浅层次的数学需求也许就仅仅是对数学中的对称、简约等美观层次的欣赏，而深层次的数学需求也许就会用射影几何等研究美术问题。

学校数学课程体系的建构需要考虑学生数学发展的不同需求，在共同诉求基础上满足学生个性化的发展需求。

三、学校数学课程建设的基本思路

根据学习力的分析，以及上述关于数学本质、学生数学发展需求的讨论，笔者将高中数学学科课程分成如图2中的四个层次，依次为补差层、基础层、拓展层、研究层。

其中补差层主要着眼于学生过去与当下的数学学习，其目的在于帮助学生尽快地跟上以及更好地学习高中数学必修内容。根据学习力中三个基础要素分成三类：知识与经验类，如《初高中数学衔接》《高中数学核心知识图解》等；思维与方法类，如《初中数学核心思想》；兴趣与价值观类，如《生活中的数学艺术》。值得说明的是，这三类课程的价值并非完全分离的，而只是更侧重于某一方面而已。比如《生活中的数学艺术》，用数学的眼光、数学的方法看待生活中也许与数学风马牛不相及的现象，其必然会涉及基本的数学知识和思维方法，但这门课程设置的核心目的在于激发起学生的数学兴趣，并通过这门课程体现数学在处理日常生活现象时独特之处，进而赋予学生数学学习的价值感。

基础层课程主要是指数学必修课程，但需要根据学生的情况进行校本化处理，具体包括课程体系的重组、课程难度的调整以及课时的调整等。《普通高中数学课程标准(实验)》将高中数学课程内容分成5大必修模块和4个选修系列，其中必修课程的模块化处理增强了重组课程体系的灵活性。而浙江省尝试将课程设置权还给学校的举措又为必修课程的校本化提供了制度保障。基于此，学校需要细致地分析本校的学情，有针对性地研究与调整必修课程。以课程体系重组为例，对于学生数学基础较好的学校，可以尝试以思维与方法为主线，强化数学内容内在的联系与逻辑，通过知识组织的大螺旋以减少同一知识的不同水平在高中学段的循环次数；而对于学生数学基础较差的学校，则可以尝试以知识与经验为主线，适当降低知识难度，注重数学活动经验的积累，通过知识组织的小螺旋以增加同一知识的不同水平在高中学段的循环次数。

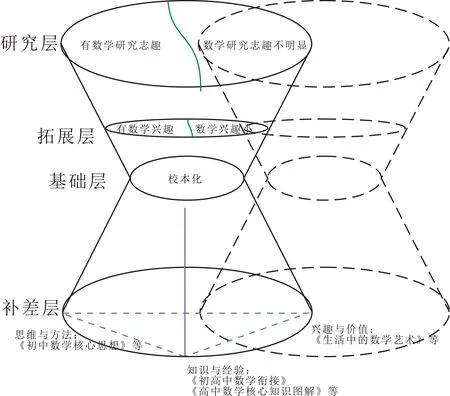
图2　学校学科课程体系示意图

拓展层与研究层课程主要着眼于学生未来发展，其中研究层课程是拓展层课程的进一步拓展与提升。基于学生未来发展的思考，笼统地将数学拓展层课程分为服务于有数学兴趣与数学兴趣不大的学生两小类，而将研究层课程分为服务于有明显数学研究志趣与没有明显数学研究志趣的学生两小类。其中，为有数学兴趣甚至有数学研究志趣的学生开设的选修课程，更强调数学思维与方法，特别是研究层课程中还强调数学研究的问题意识；而为数学兴趣不强、没有数学研究志趣的学生开设的选修课程，则更强调数学的趣味性与实用性，强调数学与其他学科的交叉(图2中的虚线图即代表其他学科的课程体系)。同样以与美术的交叉课程为例，在拓展层课程中可以开设《数学中的美学》《美术中的数学艺术》等课程，而在研究层课程中则可以开设《基于几何学的美术创作》《美术史中的射影几何研究》等课程。

前面的讨论可以发现，基础层、拓展层到研究层课程的逻辑关系均是在前一类课程基础上的进一步拓展与提升，因此这几类课程的知识覆盖面也是逐级增加的。而补差层课程则会因学校而异，对于数学生源好的学校，补差层课程的内容相对较少，反之则多。

图3　学生修读的数学课程体系示意图

但从单个学生修读的课程而言，其知识覆盖面(如图3)正好与学校整体的课程体系相反，从基础层到拓展层再到研究层是一个逐级变窄的过程。这也体现了学生由共同基础，到个性发展，再到特长发展的过程。

总之，在高中强调学生个性化发展的过程中，学校课程顶层设计极为关键，而学科课程体系的建设又为顶层设计的有效落实提供保障。本研究以高中数学课程的建设为例作了些探索，但无论在理论上还是实践层面，这方面都还是值得进一步研究的问题。

[参考文献]

[1]郭宝仙.英国普通高中课程方案及其特点[J].全球教育展望,2012,41(2):26-31.

[2]李淑文,史宁中.日本新订高中数学学习指导要领述评[J].比较教育研究,2012,(8):72-76.

[3]吴也显,刁培萼.课堂文化重建的研究重心:学习力生成的探索[J].课程·教材·教法,2005,25(1):19-24.

[4]郭黎岩,王东,田玲.提升中小学生学习力:基于脑科学的实践探索[J].中小学管理,2011,(9):4-7.

[5]张奠宙.当心“去数学化”[J].数学教学,2005,(6):14-22.

[6]张奠宙.数学思想是自然而平和的[J].人民教育,2006,(10):28-29.

[7]Ernest P.The knowledge,beliefs and attitudes of the mathematics teachers:a model [J].Journal of education for teaching,1989,15(1):13-33.

[8]黄毅英,林智中,黄家鸣等.中国内地中学教师的数学观[J].课程·教材·教法,2002,(1):68-73.

[9]张维忠,汪晓勤.文化传统与数学教育现代化[M].北京:北京大学出版社,2006:20.

[10]唐恒钧.多元文化数学与学生学习信心培养[J].宁波大学学报(教育科学版),2010,32(2):125-128.

[11]M·克莱因.古今数学思想(第一册)[M].上海:上海科学技术出版社,2002:3.

[12]G·波利亚.怎样解题[M].北京:科学出版社,1982:11.

(责任编辑张永祥/校对一心)

A Study on Mathematics Curriculum Construction in High Schools on the Basis of Learning Power Analysis

TANG Heng-jun,CHEN Bi-fen,ZHANG Wei-zhong

(College of Teacher Education，Zhejiang Normal University，Jinhua,Zhejinag,321004，PRC)

[Abstract]Diversity in education and characteristic school running have become a general trend of reforming high school education home and abroad.Curriculum construction is key to achieve this goal of education reform.Taking mathematics as an example,based on the development of mathematics learning power,this paper makes an analysis of the disciplinary nature of mathematics and the developmental demands of students fist.Then,it puts forward a multi-level categorized system of mathematics curriculum.In accordance with its functions,mathematics curriculum can be arranged into four levels:compensatory,basic,progressive and researching.Compensatory level curriculum can be categorized into three types in view of students’ current development:knowledge and experience,thinking and methodology,and interests and values.Based on students’ future development,progressive and researching curricula can be classified into two types,one for students with keen interests in and devotion to mathematics research,the other for students with little interests in mathematics and mathematical research.

[Key words]learning power of mathematics;construction of mathematics curriculum;the nature of mathematics;developmental demand of Mathematics;mathematics curriculum construction

[中图分类号]G 633.6

[文献标识码]A

[文章编号]1674-5779(2016)02-0017-05

[作者简介]唐恒钧(1979—)，男，浙江余姚人，浙江师范大学副教授，博士，主要从事数学课程与教学论研究

[基金项目]2015年教育部人文社会科学规划基金项目“民族数学与数学课程改革”(15YJA880107)成果

[收稿日期]2015-12-17