一阶线性微分方程与求导计算

桑　波

(聊城大学数学科学学院，山东聊城252059)



一阶线性微分方程与求导计算

桑波

(聊城大学数学科学学院，山东聊城252059)

[摘要]利用一阶线性齐次微分方程的求解公式， 建立了两类重要函数的求导公式，从而揭示了线性微分方程与函数导数之间的紧密联系.

[关键词]求导法则； 微分方程； 幂指函数

1研究背景

函数的求导问题是微积分的重要内容之一. 对此问题历届学生普遍反映比较困难，尤其是复杂函数的求导. 这主要是因为：一方面他们对求导公式的理解还不够深入，另一方面平时训练强度也不够.

在传统的教材体系中， 函数求导与微分方程的求解是两个相对独立的教学内容， 见[1，2，3]. 在教学实践中， 我们尝试以微分方程的观点重新审视求导公式， 以达到深入理解求导公式的目的. 通过研究发现一阶线性齐次微分方程与求导公式之间存在密切的内在联系.

fj(x)>0，fj(x)≠1， j=1，2，…，k

fj(x)>0，fj(x)≠1，j=1，2，…，k.

为可导函数， 且gj(x)为非零、可导函数. 尽管对数求导法是计算这两类函数导数的通用方法，但其求解过程仍略显繁琐.

需要指出的是， 当k=1，m1=1时， 广义幂指函数变为通常的幂指函数. 这类函数的求导方法已有一些论述[1，4，5].

2广义幂函数的求导

引理1设f(x)为非零、可导函数，则有

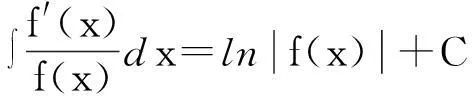
其中C为任意常数.

证只需利用第一类换元积分法和基本公式

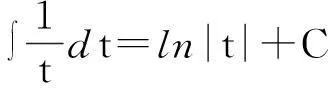
其中C为任意常数.

下面考虑一阶线性齐次方程

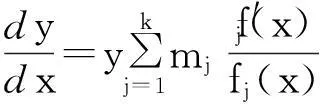
(1)

其中mj，j=1，2，…，k为非零常数，fj(x)，j=1，2，…，k为非零可导函数.

令

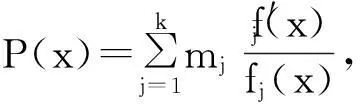
则由引理1， 方程(1)的通解为

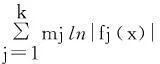
(2)

由此，得到下面的求导公式.

定理1设mj，j=1，2，…，k为非零常数，fj(x)>0，j=1，2，…，k为可导函数， 则

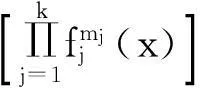
(3)

推论1设函数f(x)，g(x)非零、可导，则

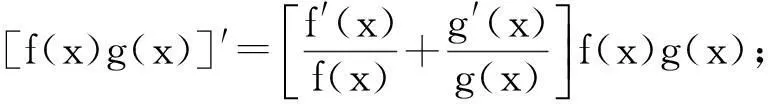
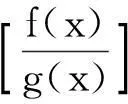
推论2设mj，j=1，2，…，k为非零常数，fj(x)>0，j=1，2，…，k为可导函数且g(x)为可导函数， 则

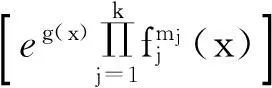
例求不定积分

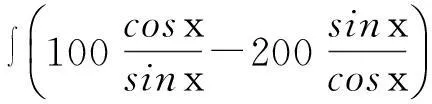
解此积分的难点在于三角函数的次数甚高， 使用常规降次的方法需要大量的计算，因此需要另辟蹊径.

由定理1

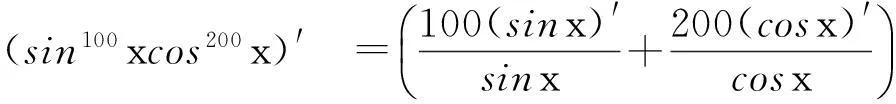
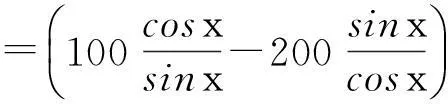
故

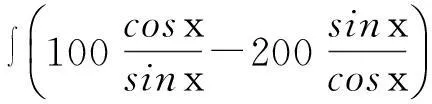
3广义幂指函数的求导

考虑幂指函数f(x)mg(x)， 其中f(x)>0，f(x)≠1，g(x)≠0，m为非零常数， 且f(x)，g(x)都可导. 为了求该函数的导数， 需要先转化为指数函数， 再利用复合函数的求导法则， 具体如下

[f(x)mg(x)]′=[emg(x)ln(f(x))]′=m[g(x)ln(f(x))]′f(x)mg(x)

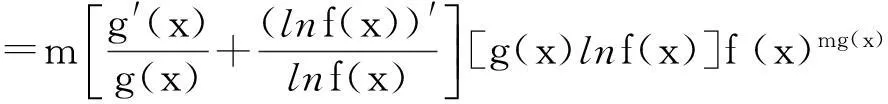
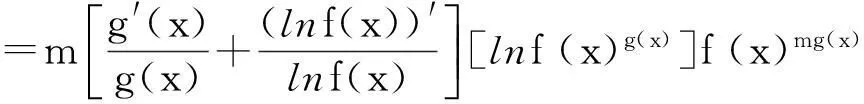
由此可得下面的引理.

引理2设f(x)>0，f(x)≠1，g(x)≠0，m为非零常数， 且f(x)，g(x)都可导，则一阶线性齐次微分方程

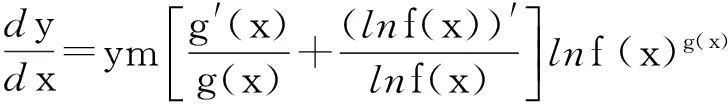
以y=f(x)mg(x)为特解.

引理3设pj(x)是连续函数，j=1，2，…，k， 且设方程

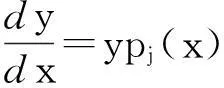
以y=hj(x)为特解， 则方程

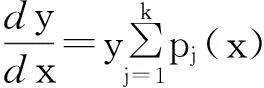
(4)

证不妨设hj(x)=cje∫pj(x)dx， 其中cj为给定的常数，则

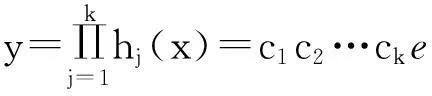
是方程(4)的特解.

定理2设fj(x)>0，fj(x)≠1，gj(x)≠0，mj为非零常数， 且fj(x)，gj(x)都可导，其中j=1，2，…，k，则方程

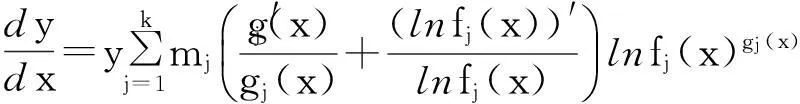
证只需直接利用引理2和引理3即可.

作为上面定理的重要推论，得到广义幂指函数的求导公式.

推论3在定理2的条件下，

[参考文献]

[1]孟广武，张晓岚，等. 高等数学[M].2版.上海:同济大学出版社，2010.

[2]韩茂安，周盛凡，邢业朋，等. 常微分方程[M].北京:高等教育出版社，2011.

[3]肖箭，盛立人，宋国强. 常微分方程简明教程[M].北京:科学出版社，2008.

[4]樊志良. 幂指函数的求导方法[J].中北大学学报，2006，27(1):8-10.

[5]汤光宋. 幂指函数导数与积分的简捷求法及其应用[J].德州学院学报，2001，17(4):4-7.

The First Order Linear Differential Equations and

the Computations of Derivatives

SANGBo

(School of Mathematical Sciences， Liaocheng University，Liaocheng 252059， China)

Abstract:Using the solution figure of the first order linear homogeneous differential equation， this paper establishes the differentiation rules for two important classes of functions， and thus demonstrates that linear differential equations are closely related to the differentiation of functions.

Key words:differentiation rules; differential equations; power exponential function

[基金项目]国家自然科学基金(11401285)；聊城大学实验技术研究基金(LDSY2014110)

[收稿日期]2014-07-20

[中图分类号]O172.1； O175.1

[文献标识码]C

[文章编号]1672-1454(2015)01-0075-03