薄膜渗透率测量模型研究
薄膜渗透率测量模型研究
周 玉 杰
(内蒙古科技大学 数理与生物工程学院,内蒙古 包头 014010)
摘要:薄膜分离技术被广泛的应用于科研、化工等多个领域。薄膜渗透率是影响薄膜性能的重要指标。本文通过数学建模的方法研究了薄膜渗透率的测定模型,并通过实验数据进行了数据拟合实验。
关键词:薄膜渗透率;数学建模;数据拟合
收稿日期:*2014-11-04
作者简介:周玉杰(1981-),女,内蒙古赤峰市人,硕士,讲师,研究方向:冶金数学建模,虚拟仿真。
中图分类号:O242.1文献标识码:A
0引言
薄膜分离技术广泛的应用于科研、食品检测、化工、纳米技术、能源和环保等众多领域。薄膜允许液体分子穿透的能力被称作薄膜渗透率。薄膜的渗透率直接决定着膜的某些功能。本文将重点研究薄膜渗透率的求解模型。
1渗透率问题的描述
假设用面积为m的薄膜将容器C分割成C1和C2两部分,在C2中注入低浓度溶液,在C1中注入高浓度溶液。这时,高浓度液体就会从C1中透过薄膜m向C2中渗透。用K表示薄膜被该物质分子穿透的能力及渗透率。求该薄膜的渗透率,其结构如下图所示:

2渗透率求解假设
为了对上面的问题进行数学建模,假设我们的研究是在以下的理想状态进行的:
(1)假设薄膜m两侧的溶液C1和C2的浓度在任何的时刻始终是均匀的。
(2)假设高浓度液体C1会透过薄膜m向低浓度液体C2中渗透。
(3)假设通过单位面积薄膜分子扩散的速度与薄膜两侧溶液的浓度差成正比。
3薄膜渗透模型的建立
设在t时刻,薄膜两侧溶液的浓度分别为C1(t)和C2(t),初始时刻两侧的浓度分别为a1和a2,单位为mg/cm3。薄膜两侧的体积分别为V1和V2,薄膜的面积为S。经过△t时间C1物质质量增加为:
V1C1(t+△t)-V1C1(t)
(1)
另外,按照薄膜渗透率的定义,C1由于渗透而减少的物质质量为:
SK(C2-C1)△t
(2)
按照质量守恒定律可知,公式1=公式2,及有:
V1C1(t+△t)-V1C1(t)
=SK(C2-C1)△t
(3)
两边同除V1△t,令△t→0, 得:
dC1(t)/dt=SK(C2-C1)/V1
(4)
在溶液通过薄膜渗透过程中,整个容器中的溶液物质的质量是不变的,所以有:
V1C1(t)+ V2C2(t)= V1a1+ V2a2
(5)
将公式5代入公式4得:
dC2(t)/dt+SK(1/V1+1/V2)C2(t)
=SK(a1/V2+a2/V1)
(6)
由于在t=0时,C2(0)=a2,可以求得:
(7)
4求解渗透率
我们在不同的时间点上对溶液的浓度进行了测量,其测量值如下所示:

表1:C 2浓度测量表
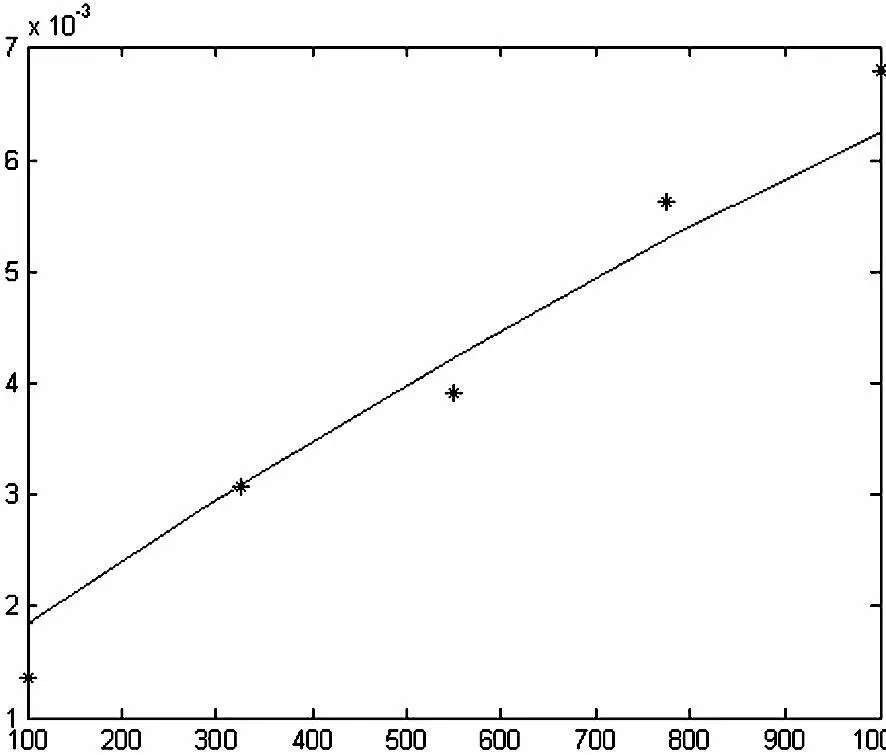
利用表1数据对公式7进行数据拟合,及求:
其拟合曲线如下图所示:
〔参考文献〕
[1]吴宗敏.径向基函数散乱数据拟合与无网格偏微分方程数值解[J].工程数学学报,2002,19(2):l-12.
[2]魏巍.MATLAB应用数学工具箱技术手册[M].北京:国防工业出版社,2004.169-229.
Study on Permeability Measurement Model of Thin Film
ZHOU Yu-jie
(School of Mathematics Physics and Biological Engineering,
Inner Mongolia University of Science and Technology,Baotou 014010)
Abstract:Membrane separation technology is widely used in many fields of scientific research,chemical industry etc. Membrane permeability is an important index to affect film properties. In this paper,through the method of mathematical modeling study on the determination of model of thin film permeability,and fit the experimental data by using the experimental data.
Key words:Membrane permeability;Mathematical modeling;Data fitting

