例说习题资源的使用——以线性代数课程为例
例说习题资源的使用
——以线性代数课程为例
张 群 英,陈 建 华
(扬州大学 数学科学学院,江苏 扬州 225002)
摘要:大学数学教与学的过程中,如何充分发挥教材习题的功能呢?本文以线性代数课程为例,通过具体案例从习题求解、合理变通和寻找联系三个层面进行了初步探究,并深度思考了在教学过程中如何将习题进行适当地引申、拓展、调整和重组,既要深入领会习题的编写意图,充分发挥习题的练习功能,又要创造性地使用习题,提高练习的有效性。
关键词:习题;功能;优化使用;矩阵;向量组
收稿日期:*2015-01-04
基金项目:江苏省研究生教改课题(教育硕士数学方法论课程问题化学习的构想与实践)(JGLX14-131)
作者简介:张群英(1975-),女,江苏省泰州人,博士,讲师,研究方向:应用数学。
中图分类号:O151.21;G642文献标识码:A
0引言
习题是学生进行有效学习的载体,大学数学课程也是如此。对于学生来说,习题是数学学习过程中不可或缺的重要环节,是学生掌握知识、形成技能、发展能力的主要载体,是沟通知识与能力的桥梁;同时也是教师了解学生知识掌握情况的主要途径。然而,在实践中,许多大学生在学习大学数学的过程中,特别是考研复习过程中,过多地关注练习卷、教辅书等课外资料,而忽视课本上的例题和习题,丢弃了很多重要的学习资源。教师对教材习题及其练习过程的设计也较少深入研究,往往只是把教材习题作为作业布置给学生,缺少对习题深度的挖掘,使得习题功能弱化,教材意图不能凸显,教学效果不尽如人意。如何帮助学生充分发挥习题功能,让学生能练出一片精彩呢?为此,我们依托线性代数课程,进行了肤浅的探究。
1案例解析
1.1从一道研究生入学试题说起
习题A设向量组α1,α2,α3线性无关,则下列向量组中,线性无关的是()。
(A)α1+α2,α2+α3,α3-α1,
(B)α1+α2,α2+α3,α3+2α2+α1,
(C)α1+2α2,2α2+3α3,α1+3α3,
(D)α1+α2+α3,2α1-3α2+22α3,3α1+5α2-5α3
该题是1997年全国硕士研究生入学考试高等数学试题,是检查学生基础知识掌握情况,具有较好区分度的一道题。
从题面看该题是关于向量组的线性相关性的判定,在与学生交流解法时发现,有一半同学是根据线性无关的定义去解题,这样做不但容易出现表述错误,而且也很费时间。仔细解读,我们应该会意识到命题者不可能让考生一种做法重复多遍。事实上,选项(A)通过直接观察很快会得到判定:第二个向量减去第一个向量就是第三个向量,即第三个向量可以通过前两个向量线性表示,当然是线性相关的。同理可以给出选项(B)的判定。关于选项(C)和(D),我们将其表述作如下改变:
联系分块矩阵运算和矩阵秩的结论,那么向量组的线性相关性取决于矩阵P,Q的秩,很快就能得到结论。实际上,这就是波利亚在总结解题时的观点:我们必须一再地变化它,重新叙述它、变换它[1]。矩阵的秩是线性代数课程的核心概念之一,在这个改变的动态过程中,学生能够感性地认识到矩阵秩的本质意义。而借助于矩阵秩来讨论向量组的线性相关性,也正是通过矩阵分块方法产生的简洁的、一般化的解法。这两者之间是有着内在关联的,教材习题就有这方面的体现,如文献[2]第四章习题19就是这一思路的课本原题,参见习题B。
习题B设向量组(B):β1,β2,…,βr能由向量组(A):α1,α2,…,αs线性表示为
(β1,β2,…,βr)=(α1,α2,…,αs)K(*)
其中K为s×r矩阵,且向量组(A):α1,α2,…,αs线性无关。证明:向量组(B):β1,β2,…,βr线性无关的充分必要条件是矩阵K的秩为r。
1.2合理变通,揭示规律深化理解
如何让学生在理解上述方法意义的基础上,感悟方法选择的灵活性、促进知识的自主建构呢? 让我们对习题B做进一步解读。
习题B条件的必要性:令B=(β1,β2,…,βr),A=(α1,α2,…,αs),则由向量组(B):β1,β2,…,βr线性无关,可得矩阵向量组(B):β1,β2,…,βr线性无关,即它的秩为r,再由r≥R(K)≥R(AK)=R(B)=r可知R(K)=r;而条件的充分性可以用反证法考虑如下:
假设向量组(B):β1,β2,…,βr线性相关,则存在不全为零的r个数l1,l2,…,lr使得(β1,β2,…,βr)(l1,l2,…,lr)T=0,即有(α1,α2,…,αs)K(l1,l2,…,lr)T=0,又因为α1,α2,…,αs线性无关,故有K(l1,l2,…,lr)T=0,这表明矩阵K的列向量组线性相关,与矩阵K的秩为r矛盾。
特别地,当r=s=n时,关系式(*)就是n维向量空间中两组基的关系,而矩阵K就为一组基到另一组基的过渡矩阵。回到试题A,那就是当α1,α2,α3是3维空间的一组基时,哪一选项中的向量组也是空间基向量组。如果能联系线性方程组理论习题B还有下列解法:
构造齐次线性方程组
x1β1+x2β2+…+xrβr=0(* *)
记X=(x1,x2,…,xr)T,B=(β1,β2,…,βr),则(* *)为BX=0,由下列充要条件:
向量组(B):β1,β2,…,βr线性无关⟺齐次线性方程组BX=0只有零解⟺
AKX=0只有零解⟺KX=0只有零解⟺R(K)=r。
问题得证。
这一解法思路来源于线性代数经典教材[3]第四章习题16。
习题C设B为r×r矩阵,C为r×n矩阵,且矩阵C的秩为r。证明:
(1) 如果BC=O,则B=O;
(2) 如果BC=C,则B=E。
1.3寻找联系,延伸拓展思维空间
综合上述三道题的思想,再融合矩阵运算,我们编拟了以下习题:
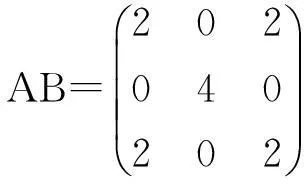
2深度思考
数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。回味案例分析过程,思索究竟如何合理有效利用课本习题,下面结合教学实践谈几点看法,与同仁分享。
2.1充分发挥习题功能,让学生练中提高
日常教学中,对于课本习题的练习,学生通常会表现出目标不明,为练而练;重视结果,忽视过程;弱化操作性习题;强调练习,忽略体验等。改变这些习惯可以在指导学生解题过程中按如下策略纠正。(1)多解求活。经常性地对学生进行一题多解的训练,对培养学生思维的灵活性和发散性是很有帮助的。譬如,改变习题呈现方式就能激发练习主动性,促进学生主动参与,让他们在参与中体验成功,在参与中体会数学学习带来的无穷魅力。(2)多变求深。如案例中设立四个问题,如果能让学生解答、分析、交流问题的思考过程,领会它们在解法上的相通之处。这样的改变,就可以帮助学生进一步提高分析问题和解决问题的能力。(3)结论延伸。如果在教学中,运用案例中提及的习题,从(A)到(C),有计划适时地介绍给学生,在学生不断感受矩阵、向量之间的规律联系,形成对“秩”的感性认识后,再安排习题D进行巩固练习。这样做,学生的思维就能得到拓展。
2.2优化使用教材习题,提高习题的利用率
课本上的习题虽经专家审定,但是教师仍然应该根据学生具备的知识和技能的实际情况选择适当的习题进行练习。
一方面,选择习题要“百里挑一”。从众多的数学习题中选择到恰到好处的习题,这就需要我们在“精”字上下功夫。精选习题的目的要明确,针对性要强。也就是说选择的习题能够对症下药。 精选习题示范性要好,选择一题要能够代表一片。例如,我们在讲解完矩阵与向量组的秩后安排如下习题:已知向量组(I)α1,α2,α3;(II)α1,α2,α3,α4;(III)α1,α2,α3,α5.如果各向量组的秩分别为R(I)=R(II)=3,R(III)=4,证明:向量组α1,α2,α3,α5-α4的秩也为4。训练的目的性和示范性就能很好地体现,从横的方面沟通了矩阵与向量组的联系、线性无关与向量组的关系,从方法看彰显了矩阵列分块的作用,矩阵初等行变换讨论秩和列向量组线性相关性的效能。
另一方面,运用习题要“以一当百”。数学习题的运用不能仅仅满足一题一解一问一答,需要我们在运用习题时注意在“活”字上做文章。同一道题,从多方面提出问题,让学生思考问题,就能够达到“练一题,带一串”的效果。同一道题,教师可结合学生实际,从不同方面启发,引导学生从不同角度去思考,用多种方法来解答,就能很好地发展学生的思维。
2.3巧用教材习题,优化学生思维品质
注意整合习题内容提高练习有效性。在教学中,我们要根据学生实际和课堂需要灵活使用教材习题,适时地对书中的习题进行调整或改编以提高学生的学习兴趣。譬如, “设A是3阶矩阵,矩阵A的每行元素之和等于3” ,提法生活化且直观,数学的理解它告诉我们3是矩阵A的一个特征值,α=(1,1,1)T是对应的一个特征向量;“β,γ是AX=o的两个线性无关的非零解”就知道0是矩阵的特征值,β,γ是对应的特征向量。 两个条件结合就提供了3阶矩阵A的全体特征值和特征向量,这种变呆板为新颖有利于激发学生的学习兴趣。
拉卡托斯曾经指出:“整个数学理论体系本身就是通过理论的不断批判和反驳而生长,通过理论的更新和竞争而取得进展的”[4](P28-29)。教学过程中,我们应该充分利用课本习题,培养学生独立思考习惯,养成善于扬弃的思维品质。
现代认知心理学家奥苏伯尔指出:"影响学习最重要的因素是学生已经知道的知识”[5](P114),因此在习题教学中,对于难度较大的习题要设计好知识铺垫,面向全体学生,力争全体学生参与知识的获取过程。让学生在练习中有成功感,培养学生良好的学习心理。
3结束语
总之,教材习题是对教学内容的巩固和发展。用好用活习题,是提高数学课堂教学效率、增强教学有效性的重要环节,需要引起教师足够关注。充分发挥习题功能,这与教师对教材的理解、教材的处理能力息息相关。对教材习题有效使用策略的选择和运用,要求教师在认真钻研习题的基础上,静心解读编写意图,精细设计练习过程,尽可能放大习题资源的教学功能,做到“题”尽其用,将习题教学演绎得更加精彩。
参考文献〔〕
[1][美] G·波利亚.涂泓,冯承天译.怎样解题:数学思维的新方法[M].上海:上海科技教育出版社,2007.
[2]同济大学应用数学系编.线性代数(第四版)[M]. 北京:高等教育出版社,2003.
[3]北京大学数学系几何与代数教研室前代数小组编,王萼芳,石生明修订. 高等代数[M]. 北京:高等教育出版社,2003.
[4][英]伊姆雷.拉卡托斯.证明与反驳[M].康宏逵译.上海:上海译文出版社,1987.
[5]李士锜.PME:数学教育心理[M].上海:华东师范大学出版社,2005.
[6]张立政.用好课本例题习题,优化学生思维品质[J].数学通报,2014,(12):22-24.
Example Research of the Use of Exercise Resources
——Taking Linear Algebra Course as an Example
ZHANG Qun-ying,CHEN Jian-hua
(School of Mathematics Science,Yangzhou University,Yangzhou 225002)
Abstract:In the teaching and learning process of university mathematics,how to make best use of the function of textbook exercises? Taking linear algebra course as an example,preliminary exploration has been studied on three levels of problem solving,reasonable accommodation and finding relations through specific case analysis. And it is also deeply analyzed on how to extend,develop,adjust and restructure the exercises appropriately in the teaching process. It’s important for students not only to thoroughly understand the writing intention of exercises and take good advantage of the practicing function of exercises,but also to creatively use exercises and improve the effectiveness of practice.
Key words:Exercises;Function;Optimum use;MatrixVvector group

