基于灰色预测模型的滑坡变形监测应用研究

基于灰色预测模型的滑坡变形监测应用研究

白 洪 伟,吴 满 意

(宿州学院 安徽省煤矿勘探工程技术研究中心，安徽 宿州 234000)

摘要：对灰色预测理论作简要介绍，并介绍灰色预测中GM(1，1)在变形监测中的理论方法。以重庆彭水县水库滑坡为例，在变形监测中分析GM(1，1)的精度和可行性。

关键词：灰色预测理论；GM(1，1)；变形监测

收稿日期：*2015-01-14

基金项目：安徽省优秀青年人才基金(2013SQRL085ZD)，宿州学院安徽省煤矿勘探工程技术研究中心开放课题(2013YKF04)，宿州学院教研项目(szxyjyxm201419)，宿州学院一般科研项目(2013yyb06)。

作者简介：白洪伟(1987-)，安徽省宿州人，硕士，助教，研究方向：测绘与3S技术。

中图分类号：O242.1文献标识码：A

0引言

滑坡的产生是地质表层的一种地质现象，也是一种严重的自然灾害，是仅仅次于地震灾害的第二大地质灾害。我国是地质灾害多发国家之一，尤以滑坡灾害的影响最为严重。每年都会因崩塌、滑坡等斜坡变形破坏给我国造成了巨大损失。据不完全统计，中国将近有70座城市和460多个县市受到了滑坡灾害的危害和威胁，平均每年经济损失至少15-23亿元。例如：水电工程中出现的滑坡等岸坡稳定问题不仅对工程的效益的正常发挥也起着重要的制约作用，而且对坝址的选择、枢纽的布置、工程的施工有着很大的控制作用。如果能够对滑坡进行变形监测,对滑坡危害进行早期预报,就可以最大限度地减少和防止滑坡灾害。

然而,关于滑坡预测和预报的应用问题的研究仍然是一个世界性难题。近年来,就如何提高滑坡预测和预报的精度,如何成功地预测预报滑坡的规模、发展趋势和发生时间问题一直被一些国内外地质工程界的专家、学者高度关注着。目前最为常用的滑坡沉降预测方法一般有：最小方差预测法、回归分析法、马尔柯夫预测法、趋势外推法、法德尔菲法等。研究结果表明，如果观测的数据较长时，以上各种数学建模方法通常都可以获得合理的预报结果。但对于数据数量贫乏时，由于信息量少且规律性不强，从而导致统计预测存在着较大难度，而且精度不高,在此情况下，灰色预测模型就具有较大的优越性。本文结合GM(1，1)模型介绍灰色预测模型在滑坡中的应用。

1灰色预测理论与GM(1,1)

1982年，华中理工大学的教授邓聚龙首先提出了灰色系统的概念，与此同时建立了灰色系统理论。灰色系统简言之就是部分信息已知，部分信息未知的系统。灰色系统理论认为，凡是有些参数已知，有些参数未知的系统都是灰色系统，如：经济系统、社会系统、生态系统等都是灰色系统。灰色系统理论能更准确地描述这些系统的状态和行为，研究基于灰色系统理论的灰色预测模型，则对这些系统预测具有重要意义。灰色预测理论最重要的模型为GM(1,1)模型,在变形监测中分为等间隔序列预测模型与非等间隔序列预测模型。实际工作中等时间的监测方法被使用较多。

1.1等间隔序列预测模型

设N元观测数列为x(0)(k)={x(0)(1),x(0)(2),…x(0)(n)}，n为序列长度(此序列一般取等时距序列，当原始数据为非等时距序列，则可采用线性差值的方法来处理，从而保证模型有较高的滤波精度)，对x(0)进行一次累加生成(1-AGO)，

(1)

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(2)

(3)

式中：

yn=[x(0)(2),x(0)(3),…,x(0)(n)]T

对生成的序列建立一阶微分方程：

(4)

式中，u,a为待估计参数，分别称为内生控制灰数、发展灰数。

令x(0)(1)=x(1)(0)，并对微分方程求解，得到GM(1，1)预测模型为：

(5)

1.2模型精度检验

对于非等间距序列和等间距序列预测模型，发展系数a值的大小都可以按照表1来确定预测模型的应用范围。

表1:发展系数 a适用范围

“早知道你们这么调皮，还不如换成那两个红紫秀才来万花谷呢！”万花谷的年轻花圣板起俏脸，眼眸里却满是笑意，脚步轻松愉快，领着他们三人往缥缈如梦的三星望月走去。

(6)

求出原始数据x(0)的方差R

(7)

残差的计算

ε(i)=x(0)(i)-x(1)(i)

(8)

残差均值的计算

(9)

残差方差的计算

(10)

后验差的比值

(11)

计算出小误差的概率p

(12)

C、P登记划分如表2。

1.3项目分析与建议

位于宿州市郊区的某滑坡处，周围有多处农户房屋和农田，为了保障周边安全和由滑坡造成的危害，为此，需要对其加强监测，预测滑坡的沉降发展趋势。现对此滑坡中监测点TP1的沉降累计值进行建模并预测，监测值为表3所示。

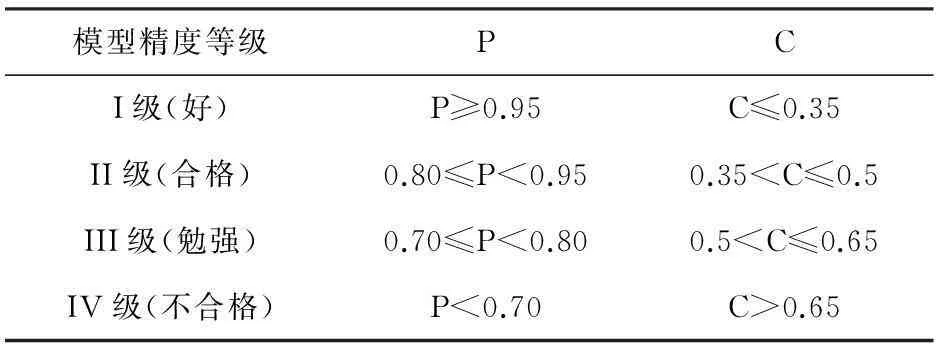
表2:预测精度等级划分

表3:变形监测点沉降量

残差为ε=(0,0.1，0.24，-0.06,0.27,0.05)，为对GM(1，1)模型检验精度，需将实际监测值与预测沉降模型值对比和后验差检验，其中，最大残差为0.27，最小残差为0，后验差比值C=0.34<0.35，小误差概率P=1>0.95，精度等级为I级，此模型是可行的，TP1所在滑坡处半个月后有裂缝，证明了模型的可行性。

通过利用GM(1,1)灰色预测模型对宿州郊区某滑坡变形数据进行的预测，得到了比较合理的结果，在实际滑坡变形监测中，如果缺少大量观测数据，也同样可以通过建立GM(1,1)灰色理论模型来进行预测预报的可行性，而且其不仅适宜于大坝修建过程中的沉降量预测，而且也适用于己竣工后的大坝的沉降量预测，并且能够达到相当高的精度。

虽然GM(1,1)灰色模型在对滑坡位移变形的预测预报中具有较高的精度，有其自身的优越性，可达到良好的预测效果，可为滑坡安全分析，防灾减灾提供可靠的预测，但在实际应用中仍然有多方面缺陷与制约性，如：如果监测的滑坡变形受多个因素影响时，就不能对其进行单纯的建模和监测，而是需要对多个因素进行综合分析，考虑各个因素的关联度，对各个因素权衡比重，进行加权分析，以达到较高精度。因此，在实际的滑坡变形预测中，还需要根据实际情况对GM(1,1)模型进行必要的修正。在一些特殊的情况下，可以将灰色模型与其他模型结合应用于滑坡的监测中，发挥两者各自的优点，以达到更及时和可靠的预测。

2结束语

本文提出了基于滑坡变形的灰色预测建立GM(1，1)模型，此模型针对滑坡变形中一些难以拟合的、随机性较大的数据进行有序的预测，具有较高的精度。在数据统计资料的基础上，对GM(1，1)模型进行了精度检验，精度达到了预期的目标，对其他模型相比，此模型有更实用的价值和更广阔的前景。

参考文献〔〕

[1]傅立.灰色系统理论及应用[M].北京:科学技术文献出版社,1992.

[2]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[3]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京: 科学出版社,2007.

[4]龙永清.高层建筑物沉降监测数据综合分析的几种方法[J].西北大学学报(自然科学版),2007,37(4):121-124.

[5]王利,张双成,李亚红.动态灰色预测模型在大坝变形监测及预报中的应用研究[J].西安科技大学学报,2005,25(3):328-332.

[6]陈伟清.灰色预测在建筑物沉降变形分析中的应用[J].测绘科学,2005,30(5):43-45.

[7]王艳慧,曹红杰,杨国祥.灰色预测模型的选择及其在大坝安全预报中应用的研究[J].地矿测绘,2001,(2):6-7.

The Application Study of Landslide Deformation

Monitoring Based on the Grey Prediction Model

BAI Hong-wei

(Anhui Province Coal Mine Exploration Engineering Technology Research Center,

Suzhou University,Suzhou 234000)

Abstract:A brief introduction to grey prediction theory,it introduces the grey prediction GM (1,1) in the deformation theory and method of monitoring. Taking Chongqing Pengshui County reservoir landslide as an example，in deformation monitoring analyse the accuracy and feasibility of GM (1,1).

Key words:Grey prediction theory; GM(1，1); Deformation Monitoring