直径限制最小生成树问题研究

直径限制最小生成树问题研究

姜娜

(内蒙古大学 数学科学学院，内蒙古 呼和浩特 010021)

摘要：直径限制最小生成树问题是一个经典的网络优化问题。本文对直径限制最小生成树问题进行了综述，介绍了该问题的研究背景、数学模型以及相关的概念，并对问题的求解方法进行了归纳总结。

关键词：直径限制；最小生成树；非完全图；BDMST

收稿日期：*2015-04-27

作者简介：姜娜(1988- )，女， 蒙古族，内蒙古通辽市人，硕士研究生,研究方向：算法分析与设计。

中图分类号：O221.7文献标识码：A

0引言

最小生成树[1](Minimum Spanning Tree 简称MST)是图论、最优化理论、算法分析与设计等诸多领域研究的重要课题，在实际问题中应用广泛，如网络设计、公交车线路设计、排水系统设计等问题；通常情况下，这些问题可转化为最小生成树问题求解。不过，单纯的生成树问题是一个理想状态，在现实应用中，随着信息技术不断提高，大数据量、高传输速度、高清晰度要求现代网络不再是简单地连通，而是要高质量的传递信息，这就要求控制成本的同时网络的连通直径也不能没有限制。为了解决这类问题，便引出了直径限制最小生成树[2](Bounded-Diameter Minimum Spanning Tree,简称BDMST)问题。

直径限制最小生成树问题在资源优化问题中应用广泛，比如网络设计中的网络直径选择，将直接影响着网络的传输速度、网络能耗以及信号传递的快慢等，在路由优化中，直径的限制，也便于设备部署的设计和维护。因此，直径限制最小生成树问题的研究，有着重要的理论和应用价值。

1BDMST问题相关概念介绍

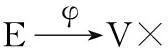
定义1.2任意两结点之间都有一条边直接相连的图称为完全图，否则，称为非完全图。

定义1.3如果V1⊂V,E1⊂E，那么图H=(V1,E1)称为G=(V,E)的子图，记作H⊆G.如果H是G的子图，且V(H)=F(G)，E(H)⊆E(G)，则称H是G的生成子图或支撑子图。

定义1.4结点与边交替出现的序列v0e1v1e2，…，v1，称为结点v0到v1的链。其中，结点vi-1和vi是边ei的两个端点(i=1,2,…,l)。称结点v0为链的始点，结点v1为链的终点。链中边的条数称为链长度。

若链中边各异，则称为迹；若链中结点各异，则称为路。若v0=vl称为闭的，否则称为开的。闭的路径称为圈。

定义1.5如果图G中每一对结点之间都有一条路连接，则称图G是连通图，否则，称G是非连通图。

定义1.6若图G中存在从结点u到结点v的路径，其中路径长度最小的那条称为u到v的最短路径，其长度称为u到v的距离，记作dG(u,v) 。

定义1.8设图G是连通图，对它的每条边都赋予一个数值，称之为边的权值，边e1的权值记为wi=w(ei),i=1,2,…,m，全部边的权值w={w1,w2,…,wm}，赋予权值的图称为赋权图或网络。

定义1.9对于图G的任一子图H，图H的权值w(H)定义为其边的权值和，设T是图G的生成树，且权值在G的所有生成树中最小，则T称为图G的最小生成树。

定义1.10设T是图G的生成树，D是直径限制，若树T的直径DT满足要求的直径限制(DT≤D)，则称T为图G满足直径限制的生成树，若T还是所有满足直径限制的生成树中具有最小权的树，则T称为图G的直径限制最小生成树。

2BDMST问题的数学模型

给定连通的赋权无向图G=(V,E,W)，其中V表示图的顶点集，E表示图的边集，W是图的边的权值。设S为G的所有生成树的集合，T是G的一个生成树，DT是树T的直径.设D是G的生成树的直径限制，因此，BDMST问题的数学模型[3]为：

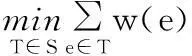
s.t.DT≤D

显然，BDMST问题就是要从集合中找到满足直径限制且权值最小的生成树。

3求解BDMST问题算法

直径限制最小生成树问题是派生出来一个组合优化问题，相比求解度约束最小生成树问题 (Degree Constrained Minimum Spanning Tree Problem，DCMST)的算法，求解BDMST问题算法要少的多，当直径限制D=2、D=3时，是简单问题，通过逐点的多项式的时间里就可以得到最优解。当直径限制D≥n-1时，这个限制没有实际约束力，因为n个结点的树，直径不会大于n-1，所以就是标准的最小生成树问题。而当直径限制D∈[4,N-1)时，BDMST问题是一个NP难问题[4]。求解BDMST问题的算法可以归为三大类：精确算法，快速算法以及现代优化算法。

3.1求解BDMST问题的精确算法

对于求解BDMST问题的精确算法，有依据线性整数规划[5,6]求解直径限制最小生成树问题的方法，以及Gruber和Raidl提出来了一种基于0-1整数规划的分支定界算法[7]，对于这些精确算法，常常适应于求解小规模的问题，而对于一些规模较大的问题则会失效。

3.2求解BDMST问题的启发式算法

启发式算法是一种适合较大规模问题的快速算法，应用非常广泛。求解BDMST问题比较常见的启发式算法有：2000年Deo和Abdalla[8]提出的一次性构造生成树算法(简称OTTC算法)，此算法和Prim算法很相似，在每次迭代过程中，选择那些未连接的距离最近的点，在不违背直径的基础上将其连接到树中；而在对OTTC算法改进的基础上，2003年由Raidl和Julstromy[9]提出了一个随机贪心算法(Random Greedy Heuristic Algorithm，简称RGH算法)，此方法从随机选择一点作为中心点开始，然后从剩余的顶点中随机地选择，并通过权值小的边连接进入，这样就从中心拓展了生成树；2004年，Julstromy[10]又对RGH算法进行了改进，提出了以中心为基础的树的结构算法(Centre-based tree construction,简称CBTC)，它也使用了中心的概念，不过在每次迭代过程中，它选择那些未连入的且距离最近的点，这些被选取的点保证在部分结构树中的直径限制。上述几种启发式算法，在文献[10]中对它们进行了验证，结果显示：在欧式空间，RGH要比OTTC、CBTC得到的结果好一些，而在欧式空间以外的空间，结果则刚好相反。

3.3求解BDMST问题的现代优化算法

现代优化算法，与启发式算法类似，可以求出其近似解，并接近于其准确解， 在现代优化算法中，比较经典的当属遗传算法，对于求解BDMST问题的遗传算法而言，比较典型的有：2003年由Raidl和Julstromy提出的基于边集编码的遗传算法[11](Edge-coded Genetic Evolutionary Algorithm,简称JR-ESEA)和基于序列编码的遗传算法[12](Permutation-coded Evolutionary Algorithm，简称JR-PEA)，一般来说，JR-PEA得到的结果要比JR-ESEA得到的结果好，不过它耗时相对有点长。此外还有利用随机键去表示[13]的遗传算法，此算法与JR-PEA有许多的相似之处。在文献[14]中Gruber提出了四种邻近搜索，2006年Raidl和Julstromy将这些邻近搜索应用于蚂蚁算法(Ant Colony Optimization,简称ACO)[14,15]。2008年Binh,Nguyen以及McKay[15]提出了一种新的混合遗传算法(New Hybrid Genetic Algorithm,简称HGA)，其主要的思想是：多个种群进行交配，对每个种群利用经典的启发式算法进行初始化，并利用边集进行编码。

对于求解BDMST问题除了上述算法还有许多算法，比如基于中心的聚类算法(Center-Based Recursive Clustering,简称CBRC)[16]以及对RGH、OTTC的改进算法[17]等。

4总结和展望

直径限制最小生成树问题是NP-Hard问题，寻找有效的算法是研究的核心问题。对于大规模问题，目前已有的方法，大多是采用启发式算法或遗传算法等现代优化方法求解，且基本是以完全连通图为前提，但在实际应用中还是以非完全图居多，研究非完全图下BDMST问题的算法更有实用价值。

参考文献〔〕

[1]Gary.Chartrand,Ping Zhang(著).范益政,汪毅,龚世才等(译).图论导引[M].北京:人民邮电出版社,2007.81-86.

[2]石磊,冯祖针,杨建强.度、直径约束最小生成树问题及其算法[J].云南民族大学学报(自然科学版),2012,21(4):295-297.

[3]Binh.H.T.T,McKay.R.I,Nghia.N.D ,etc.New Heuristic and Hybrid Genetic Algorithm for Solving the Bounded Diameter Minimum Spanning Tree Problem,in Proceedings of Annual Conference on Genetic and Evolutionary Computation [J].Montréal,2009,25(5):373 -380.

[4]Garey M.R,Johnson D.S.Computers and Intractability: a Guide to the Theory of NP-Completeness[J].SIAM Review,1982,24(1): 90-91.

[5]Achuthan.N.R,Caccetta L,Caccetta P,etc.Computational Methods for the Diamter Restricted Minimum Weight Spanning Tree Problem[J].Australian Journal of Combinatorics,1994,10(2):379-384.

[6]Gouveia.L,Magnanti T.L,Requejo C.A2-Path Approach for Odd Diameter Constrained Minimum Spanning and Steiner Trees[J].Networks,2004,44(4):254-265.

[7]Gruber.M ,Raidl G.R.A new 0-1 ILP Approach for the Bounded Diameter Minimum Spanning Tree Problem,in Proceedings of the Second International Network Optimization Conference [J].Vienna,2005,15(3):1-8.

[8]Deo.N,abdalla.A.Computing a Diameter-constrained Minimum Spanning Tree in Parallel[J].Lecture Notes in Computer Science,2000,15(4):17-31.

[9]Julstrom B A.Greedy Heuristic for the Diameter-Constrained Minimum Spanning Tree Problem[J].Journal of Mathemation Sciences,2009,161(6): 930-943.

[10]Alok Singh·Ashok K.Gupta.Improved Heuristics for the Bounded-diameter Minimum Spanning Tree Problem[J].Soft Computer,2007,11(10): 911-921.

[11]Raidl G.R,Julstrom B.A.Greedy Heuristics and an Evolutionary Algorithm for the Bounded-Diameter Minimum Spanning Tree Problem[J].Proceeding of the 2003 ACM Symposium on Applied Computing,2003,102(5):747-752.

[12]Julstrom.B.A,Raidl G.R.A Permutation Coded Evolutionary Algorithm for the Bounded Diameter Minimum Spanning Tree Problem[J].Proceedsing of the Genetic and Evolutionary Computation Conference,2003:2-7.

[13]Julstrom B.A.Encoding Bounded-diameter Spanning Trees with Permutations and with Random Keys[J].Lecture Notes in Computer Science,2004:3102,1272-1281.

[14]Martin Gruber,Jano van Hemert,Güntheer r.Raidl.Neighbourhood Searches for the Bounded Diameter Minimum Spanning Tree Problem Embedded in a VNS,EA and ACO.USA Copyright[J].Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation,2006:1187-1194.

[15]石磊,冯祖针,杨建强.蚁群算法求解直径约束最小生成树问题[J].红河学院学报,2012,10(4):16-18.

[16]Huynh Thi Thanh Binh,Nguyen Xuan Hoai,R.I.McKay.A New Hybrid Genetic Algorithm for Solving the Bounded Diameter Minimum Spanning Tree Problem[J].Proceedings of IEEE World Congress on Evolutionary Compution,2008,24(5):3128-3134.

[17]玄光男,程润伟(著).于歆杰,周根贵(译).遗传算法与工程优化[M].北京:清华大学出版社.2003.1-10.

[18]熊小华,宁爱兵,马良.基于降阶的最小生成树快速算法[J].计算机应用研究,2010,27(6):2051-2053.

Overview of Bounded-diameter Minimum Spanning Tree Problem

JIANG Na

(Faculty of Mathematical Sciences,Inner Mongolia University; Hohhot 010021 )

Abstract:Bounded-diameter minimum spanning tree problem is a classic combinatorial optimization problem.This paper reviewed the bounded diameter minimum spanning tree problem,at the same time,it introduced the research background mathematical models and concepts and summarized this problem solving algorithm.

Key words:Bounded-diameter;Minimum spanning tree ;Non-complete graph；BDMST