一类定积分的换元积分法

一类定积分的换元积分法

徐 国 明

(包头师范学院 数学科学学院,内蒙古 包头 014030)

摘要：本文在已有定积分的计算方法之上，结合积分的上、下限进行换元，从而简化了定积分的计算，进一步完善了定积分的计算方法。

关键词：定积分；换元积分法；计算

收稿日期：*2014-10-16

基金项目：包头师范学院本科教学改革研究课题(BSJG13Q005)

作者简介：徐国明(1982-),内蒙古赤峰人，硕士，研究方向：生物数学。

中图分类号：O186.13文献标识码：A

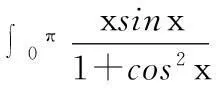
证明：令t=a+b-x,则x=a+b-t,所以

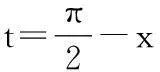
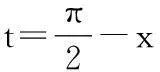
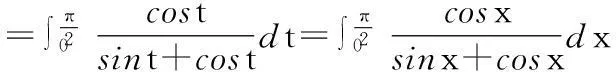
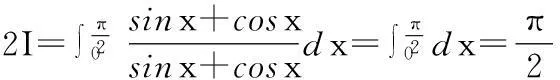
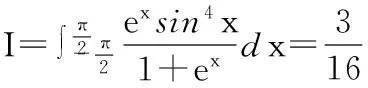
解：令t=-x，则x=-t，所以

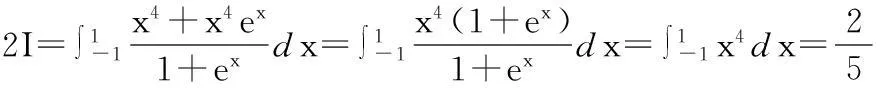
对于对称区间上定积分的计算，需要考察被积函数的奇偶性，利用

来计算，但是当被积函数既不是奇函数也不是偶函数时，通过例3、例4可以发现，可以利用定理介绍的方法采用相反数换元来解题。

参考文献〔〕

[1]李永兴.定积分计算与思维品质培养[J].数学教育学报,1996,5(2):76-78.

[2]刘玉琏，傅沛仁.数学分析讲义[M].北京：高等教育出版社，2005.

[3]华东师范大学数学系.数学分析[M].北京：高等教育出版社，2008.

[4]韩仲明.定积分的计算方法与技巧[J].数学教学与研究，2011,53:80-81.

[5]罗威.定积分计算中的若干技巧[J].沈阳师范大学学报(自然科学版),2010,10(2):165-168.

A Kind of Definite Integral in Integration by Substitution

XU Guo-ming

(Faculty of Mathematics,Baotou Teachers College,Baotou 014030)

Abstract:The article is based on the existing calculation method of the definite integral,and combined with the integration of the lower limit as well as the upper limit to exchange element,which simplifies the calculation of definite integrals,at the same time,further improved the calculation method of definite integral.

Key words:Definite intergral;Integration by Substitution;Calculation