盲校数学教学中发展学生空间观念的几点思考

魏亚萍

摘 要：培养盲生空间观念有着重要的现实作用，不仅有助于盲生中学几何课的学习，发展空间思维能力，还有助于盲生更好地认识、理解生活空间，更好地生存与发展。在课堂教学实践中结合新课程理念，在案例积累的基础上，探索思考发展盲生空间观念的几种方法：立足于学生的生活经验和已有的数学活动经验感悟，在图形概念中领悟，在“体”“面”转换中感悟，通过代数关系表述几何问题的方法领悟。

关键词：盲生;数学;空间观念;培养

空间观念的建立是提高学生数学素养的重要标志，有助于学生数学地理解和解释现实问题，同时也有助于学生提出问题和解决问题能力的提高。帮助学生建立空间观念是数学教育的重要任务。《义务教育数学课程标准（2011年版）》明确指出：“空间观念主要是指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体，想象出物体的方位和相互之间的位置关系，描述图形的运动和变化，根据语言描述出图形等。”《盲校数学课程标准》也指出：“要丰富对现实空间及图形的认识，建立初步的空间观念，发展形象思维。”数学课程标准在三个学段中均安排了与“图形与几何”相关的内容目标。

空间观念有助于概念的形成，有些空间观念可能终身作用于我们的大脑，帮助我们去解决实际问题和认识现实世界。它是人们更好地认识和描述生活空间并进行交流的重要工具。培养盲生空间观念有着更重要的现实作用，不仅有助于盲生在中学几何课的学习，发展空间思维能力，还有助于盲生更好地认识、理解生活空间，更好地生存与发展。在初中数学中，很多内容都需要学生具备空间观念，而空间观念是盲生缺乏的，盲生在几何知识的学习凸显出困难，尤其是在图形的运动教学中更为难。在培养盲生空间想象能力的过程中会遇到其空间识别力低、生活经验有限、空间形象感知力差等障碍。笔者在从事盲校初中数学教学中一直在思考：我们怎样运用有效手段培养盲生的空间观念？应怎样选择有利于培养盲生空间观念的内容、途径和教学方法？

在人类获得的外界信息中，80%来自视觉。然而，盲生还有听觉、触觉、动觉、嗅觉和味觉等，这些感知觉在他们的生活学习中起着重要的作用。在视力障碍教育中，缺陷补偿训练运用在盲生各个方面的学习。以手代眼训练、学会运用其他器官、空间能力训练、对实物具体形象的认识。那么笔者在空间观念培养的教学中会经常从盲生的角度去设计教学活动，以下是笔者在教学中的几点思考。

一、立足于学生的生活经验和已有的数学活动经验感悟空间观念

数学图形作为一种结果，它是静止的、固定的、清晰的，但作为一种活动，它又是动态的、可创造的、可操作的，所以在设计教学过程时，我总是尽量让学生在学习的过程中动起来，尽量使他们处在亢奋的状态。有时我把自己设想成盲生，以学习者的身份设计一些探索性活动，思考哪些设计能够使盲生高兴去做，哪些设计能够诱使盲生展开探究，使他们在动脑的同时，身体也适当活动，使得思维实验与操作实验和谐相处，从而提升自己的智能水平。

下面以《等腰梯形的性质的探索及证明》的教学为例来说明。

首先，我让盲生利用平行四边形纸片剪梯形，再利用矩形纸片剪特殊梯形，而后利用剪出的等腰梯形研究发现等腰梯形的性质。这样设计的目的，如课程标准中所说的“数学教学是数学活动的教学”。

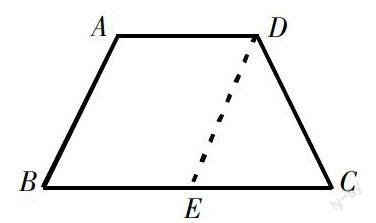
然后，让盲生在泡沫板上演示——在等腰梯形ABCD中，过点D作线段AB的平行线，将这个梯形分别分割成了什么图形？

让盲生想象：任意梯形、直角梯形这样分割，分别分割成什么图形？

（撬动学生的思维杠杆：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决。这为后面利用辅助线解决问题做好铺垫。）

接着，让盲生继续自主探索、提出猜想：提供给每个学生一个等腰梯形的纸片，让学生用各种数学工具通过各种数学方法，如翻折、旋转等来探索等腰梯形有哪些性质。学生动手、思考、讨论交流后说出自己的方法。

笔者在教学中尽量避免使学生习惯与简单地接受或被动地工作，而是尽量用任何方法激发学生的主动性。本节课把数学活动贯穿于整个教学活动始终，学生参与程度高，教师没有一味地照本宣科，而是在教学中设计了直观情境，呈现形象材料，让学生在操作中发现，在操作中探究，在操作中升华。通过问题的情境设计—探索结论—论证—应用性质，让学生经历认知的过程，提高学生的学习能力。在学习过程中，学生进行小组合作学习与交流活动，通过学生自主合作的探索，获得新知。课堂教育必须加强盲生参与机会，提高参与的质量与能力，使盲生真正成为教学的主体，以达到发展盲生个性以及培养盲生思维的深刻性和广阔性的目的，在实践操作过程中也提升了空间观念。

二、在图形概念中领悟空间观念

“能描述实物或几何图形的运动和变化”是空间观念在分析和抽象层次上的表现，在中学阶段，几何变换主要表现在平移、旋转和轴对称上。如，学生对平移（旋转）基本概念的掌握情况会影响学生对一种运动是否平移（旋转）的判断。

例如，盲生对“平移”概念的理解，笔者设计以下题目。

请判断以下运动是否是平移，并说明理由：

1.吊扇风叶的转动。

2.弹簧的拉伸。

3.钟摆的摆动。

4.电梯的上升。

要判断一种运动是否是平移，必须满足三个条件：所有点都进行移动;每一个点移动的方向相同;每一个点移动的距离相同。有的学生认为钟摆的摆动是平移：“这很符合定义啊，所以点都动了并且还是一个方向，所以是平移。”“它每次摆动时摆动的距离都是一样的。”这样的学生是因为没有理解平移的概念（只有同时满足三个条件的运动才是平移），所以才会出现这样的错误。这提示我们在教学过程中还要加强盲生对基本概念的理解。

三、在“体”“面”转换中感悟空间观念

在图形的认识中，从立体到平面便于盲生从直观的图形中观察并抽象出平面图形，从平面再回到立体，这是一个知识经历“初步认知表象—探究问题实质—升华感性认识”的过程，让盲生经历立体与平面之间的相互转换，符合学生的认知规律，有利于盲生对图形形成更深层的认识，便于盲生对知识进行梳理及升华，有利于盲生发展空间观念。

教学“弧长和扇形面积（二）”时，笔者这样设计：

1.课前让每个学生动手剪出一个扇形，然后将它卷成一个圆锥体。

2.触摸圆锥模具，请学生说出圆锥有哪些特征。

3.回答：连接圆锥顶点与底面圆任意一点的线段都是母线，圆锥的母线应具有什么性质？

4.想象：把圆锥的侧面沿它的一条母线剪开，展在一个平面上，这个展开图是什么图形？

空间观念进一步发展，逐步形成空间想象力，空间想象依赖于空间感知，盲生经历动手做、观察、想象等认识过程是非常必要的，只有这样，才能充分发挥盲生的空间想象能力，盲生的空间观念才会得到升华。

四、通过代数关系表述几何问题的方法，领悟空间观念

数形结合是在解决几何图形问题时，利用数量特征将其化为代数问题，而在解决与数量相关的问题时，又考虑其结构的特点，将其化为几何图形问题。“数”与“形”紧密联系有利于更好地理解、掌握数学知识。数形结合是贯穿在整个中学教学中的一种重要数学思维方法，可培养学生的数学思想方法的意识和能力，锻炼学生的思维品质。盲生的代数学习优于几何学习，用数量关系来理解几何问题能帮助盲生领悟空间观念。

例如，教学“勾股定理”时，笔者利用拼图游戏验证定理，体会《赵爽弦图》的原理。

1.让学生动手将四个全等直角三角形围成一个大正方形，中间的部分是一个小正方形，（通过手动促使脑动）如下图所示：

2.提问：如果a表示较短直角边，b表示较长直角边，c表示斜边，你能用此图证明勾股定理吗？

讨论结果：∵c2=4×ab+（b-a）2

化简，得c2=2ab+a2-2ab+b2=a2+b2

∴c2=a2+b2

拼图活动发展学生的形象思维，建立初步的空间观念，再用代数公式给出证明，使学生对勾股定理的理解更加深刻和确信结论的正确性，同时体会数学中数形结合思想，使学生深化理解代数与几何之间的联系。

培养盲生的空间观念，要让他们有充分的时间和空间观察、测量、动手操作，对周围环境和实物产生直接感知，这需要大量的实践活动，这些都离不开自主探索、亲身实践、观察、操作、归纳、类比、猜想、变换、直观思考等重要的手段。笔者在课堂教学实践中结合新课程理念，在案例积累的基础上，探索思考发展盲生空间观念的方法，力求在课堂教学活动中，采用有效方法，使不同的学生在数学上得到不同的发展。

参考文献：

[1]雷珮瑛.发展学生空间观念的五种方法[J].教育导刊，2012（08）.

[2]乔廷强.对发展学生空间观念的几点思考[J].中国教育技术装备，2010（22）.

[3]蔡和平.如何培养学生的空间观念[J].吉林教育，2011（25）.