一计不成另生一计

王裕龙

解题既意味着转化，既把生疏问题转化为熟习问题，把抽象问题转化为具体问题，把复杂问题转化为简单问题，把一般问题转化为特殊问题，把高次问题转化为低次问题；把未知条件转化为已知条件，把一个综合问题转化为几个基本问题，把顺向思维转化为逆向思维等，因此学会数学转化就是学会不断变换思维，即一计不成另生一计 ，从而有利于实现学习迁移，较快地提升学习能力.

一、“一般——特殊”的表示转化

在解决三角形角度的有关问题时，我们常通过设未知数，列出方程（组）解决.

例1 在△ABC中，已知∠A：∠B=1：3，∠B：∠C=3：5，求∠A、∠B、∠C的度数.

【分析】要求出∠A、∠B、∠C的度数，我们可以从已知条件中∠A、∠B、∠C之间的关系，设∠A=x，则∠B=3 x，∠C=5 x，再根据三角形三内角和等于180°列出方程，求出x的值，得∠A、∠B、∠C的度数.

【点评】当题目中出现比值条件时，我们一般设其中一份为x，不同的角转化为用相同字母表.

如果将∠B：∠C=3：5改为∠B：∠C=2：4，其他条件不变，求此时∠A、∠B、∠C的度数.

二、“无关——关联”的整体转化

在解决三角形角度的有关问题时，常利用整体处理法，把复杂的问题简单化，将看似无关的条件转化为有关联的条件.

例2 如图，∠A 为60°的三角形纸片，剪去这个60°角后，得到一个四边形，则∠BDE+∠CED的度数为 （ ）

A.120° B.180° C.240° D.300°

【分析】要求∠BDE+∠CED的度数，根据平角的定义，∠BDE+∠CED =360°-（∠ADE+∠AED），把∠ADE+∠AED看做整体，而求∠ADE+∠AED的度数，由已知条件∠A=60°，根据三角形三内角和等于180°，就可以很容易的求出，最后求得∠BDE+∠CED的度数.

【点评】本题是求两个角的度数之和，不能把每个角的度数求出来，我们用“整体”来转化要解答的问题.选C.

三、“分散——集中”的位置转化

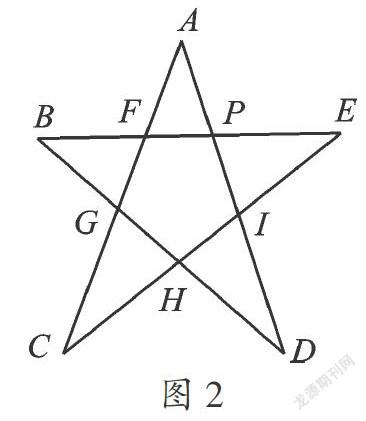
例3 如图， 求出下边星形中 ∠A+∠B+∠C+∠D+∠E的度数.

【分析】求∠A+∠B+∠C+∠D+∠E的度数，咋一看，不知如何下手，那么我们可以把这些“分散”的角“集中”起来，这里利用三角形一个外角等于不相邻两内角和，得到∠CFB=∠C+∠E，∠DPE=∠B+∠D，最后由对顶角相等，这样就转化成求三角形三内角和.

【点评】求五个角的和转化为求一个三角形的内角和，实现生疏问题转化为熟习问题.你还有其他的转化途径吗？请跟同伴交流.

四、“陌生——熟悉”的构造转化

例4 一个零件的形状如图所示，按规定：∠CAB=90°，∠B和∠C应分别是 32°和21°.检验工人量得∠BDC=148°，就断定这个零件不合格.请运用三角形的相关知识说明零件不合格的理由.

【分析】要判断零件不合格，就是要求得∠BDC不等于148°，也就是要求出∠BDC的度数，我们需要添加辅助线将四边形的问题转化为三角形问题，根据三角形一个外角等于不相邻两内角和得到∠BDC的度数.

【点评】本题将实际问题转化为数学问题，再将四边形问题转化为三角形问题.你还有其他解法吗？请告诉自己的小伙伴.

（作者单位：江苏省常熟市王庄中学）