直面中考 启迪思维

姜炜

《平面图形的认识（二）》这章内容是中考的重点基础知识，有时单独命题，有时与后面知识综合考查.近年中考中常见以下几类问题.

一、平行线的性质与判定

例1（2014·江苏无锡）如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（ ）.

A.∠1=∠3 B.∠2+∠3=180°

C.∠2+∠4﹤180° D.∠3+∠5=180°

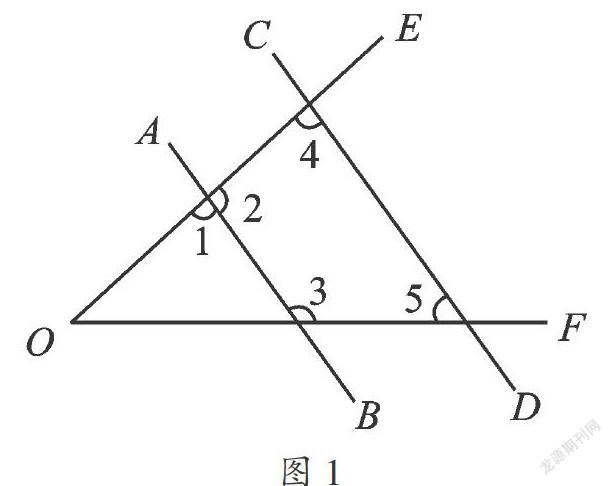
【分析】根据平行线性质进行判断即可.

【解答】选项A，∠1与∠3是射线OE与OF被直线AB所截得的内错角，而OE与OF不平行，故本选项错误；选项B，∠2与∠3是射线OE与OF被直线AB所截得的同旁内角，而OE与OF不平行，故本选项错误；选项C，因为AB∥CD，所以∠2+∠4=180°，故本选项错误；选项D，因为AB∥CD，所以∠3+∠5=180°，本选项正确.故选D.

【点评】解决此类问题关键在于牢记平行线的性质，正确辨识图形，判断直线与角的关系.

二、三角形的三边关系

例2（2013·江苏南通）有3cm，6cm，8cm，9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为（ ）.

A.1 B.2

C.3 D.4

【分析】从4条线段中任取3条进行组合，共有4种情况.分别判断每种情况能否组成三角形即可.

【解答】四条木棒的所有组合：①3，6，8；②3，6，9；③3，8，9；④6，8，9.第二组3+6=9，因此3，6，9不能组成三角形.故选C.

【点评】学会判断三条线段能否组成三角形：只要看较短的两条线段的长度和是否大于最长线段的长度.此外，如何按照一定顺序不重不漏地列举出可能出现的情况，值得思考.

例3（2012·江苏徐州）如果一个三角形的两边长分别为6和9，则第三边长可能是（ ）.

A.2 B.3

C.7 D.16

【分析】已知三角形的两边长分别为6和9，可根据三角形任意两边之和大于第三边，求出第三边范围.

【解答】设这个三角形第三边长为x，则由三角形三边关系得9-6﹤x﹤9+6，即3﹤x﹤15.选项中2，3，16都不符合，只有7符合.故选C.

【点评】已知三角形两边，第三边的取值范围是大于其他两边之差且小于其他两边之和.

三、多边形的边数

例4（2013·江苏扬州）一个多边形的每个内角均为108°，则这个多边形是（ ）.

A.七边形 B.六边形

C.五边形 D.四边形

【分析】由题意，这是一个正多边形，它的内角和等于一个内角的度数乘以内角个数.

【解法一】设这个多边形有n条边，由于每个内角均为108°，故内角和可表示为108° n，由题意得108°·n=（n-2）·180°，解得n=5.

【解法二】设这个多边形有n条边，由于每个内角都为108°，则每个外角为180°-108°=72°，外角和可以表示为72°·n，由题意得72°·n=360°，解得n=5.

【解法三】因为这个多边形每个内角均为108°，所以每个外角为180°-108°=72°，边数为360°÷72°=5.故选C.

【点评】求多边形的边数问题，设边数为n，寻找等量关系列方程是一种方法.由于多边形的外角和是固定不变的，因此对于正多边形，我们可以把已知的内角转化为外角，来求边数.

四、有关角的度数计算

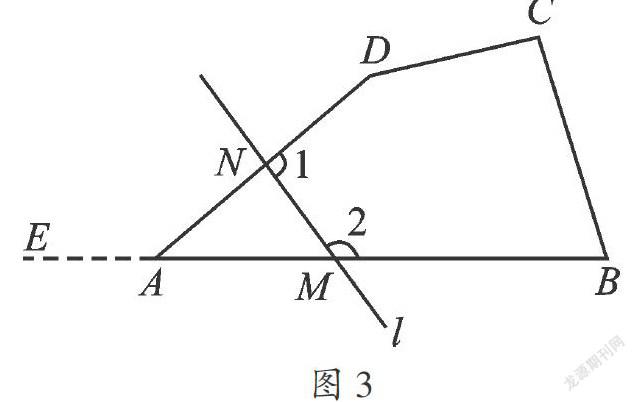
例5（2013·四川乐山）如图，四边形ABCD中，∠A=45°，直线l与边AB，AD分别相交于点M，N则∠1+∠2= .

【分析】根据题意，我们没有办法分别求出∠1与∠2的度数.因此我们将∠1+∠2看作一个整体来计算.∠1与∠2可以看作是△AMN的两个外角，也可以看作五边形MBCDN的两个内角.

【解法一】延长线段BA到点E.由于∠BAD=45°，所以∠EAD=180°-45°=135°，故∠1+∠2=360°-∠EAD =360°-135°=225°.

【解法二】在四边形ABCD中，∠A=45°，所以∠B+∠C+∠D=360°-45°=315°，在五边形MBCDN中，∠1+∠2+∠B+∠C+∠D=（5-2）×180°=540°，所以∠1+∠2=540°-315°=225°.

【点评】注意整体思想.本题的关键是将∠1+∠2看作一个整体，放在哪一个位置去看.

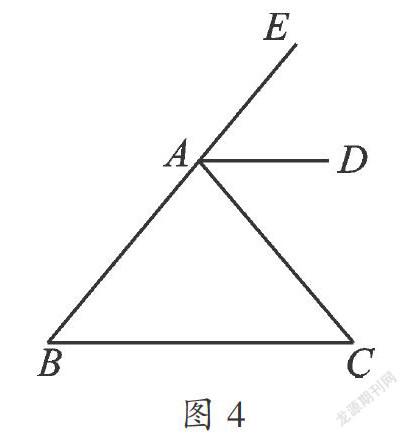
例6 （2013·江苏镇江）如图，AD平分△ABC的外角∠EAC，且AD∥BC，若∠BAC=80°，则∠B= .

【分析】要求∠B，我们一方面看看由已知能够得到些什么，另一方面由结论入手去寻找与∠B有关的角.

【解法一】因为∠BAC=80°，所以∠EAC=180°-80°=100°，又因为AD平分∠EAC，所以∠EAD= ∠EAC=50°，因为AD∥BC，所以∠B=∠EAD=50°.

【解法二】设∠B=x°，因为AD∥BC，所以∠EAD=∠B=x°，因为AD平分∠EAC，所以∠DAC=∠EAD=x°，因为AD∥BC，所以∠B+∠BAD=180°，所以x+80+x=180，x=50，即∠B=50°.

【点评】解法一由已知出发，顺藤摸瓜，一步步求出未知角；解法二从未知角入手，结合已知条件，找寻与未知角有关的角.事实上我们都是运用平行线的性质将已知角与未知角联系了起来.因此，平行线中有关角的计算问题，通常考虑利用平行线性质将角进行转换，并结合运用对顶角、角平分线、三角形内角和等知识.

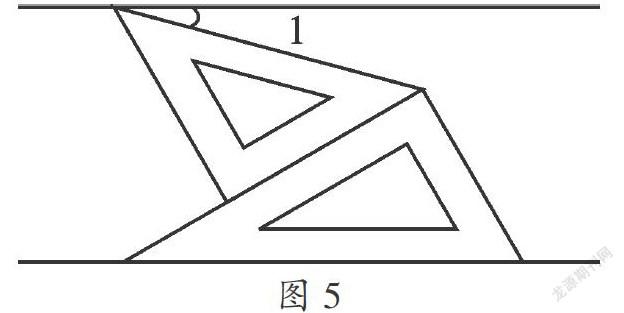
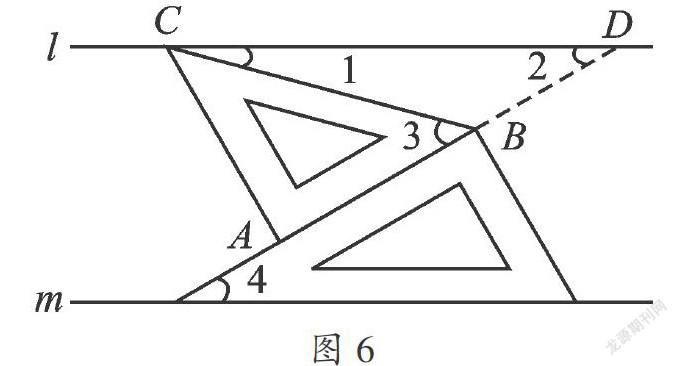
例7（2013·辽宁盘锦）如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（ ）.

A.30° B.20° C.15° D.14°

【分析】纸条对边平行，可是图中没有这两条平行线被第三条直线所截的同位角、内错角或是同旁内角，因此考虑添辅助线构造基本图形.

【解答】延长线段AB与直线l交于点D.因为l∥m，所以∠2=∠4=30°，又∠CBD=180°-∠3=180°-45°=135°，所以

△CBD中，∠1=180°-30°-135°=15°.故选C.

【点评】三角板、直尺叠放问题在近两年各地中考题中经常出现，要注意挖掘隐含条件，必要时添加辅助线.