握手的次数

范敏祎

我们经常会碰到有关求多边形对角线条数的问题，那么这样的问题该怎么去解决，如何去思考呢？

首先我们可以通过画图来找到关于多边形对角线的规律

例如： 四边形对角线有2条 五边形对角线有5条.

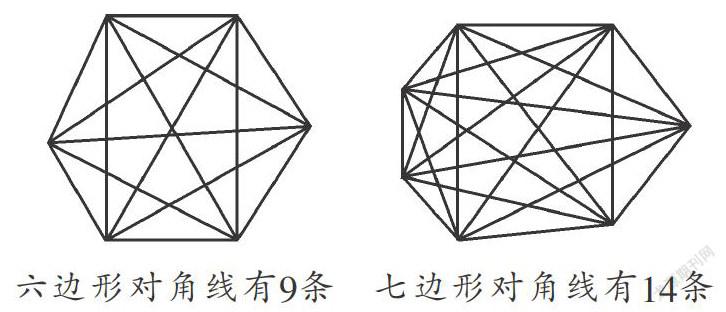
可以看到，2，5，9，14……这些数字背后存在着规律，我们可以根据这些规律去解决问题.那么，有没有简单一点的方法呢？我们可以从多边形对角线的定义来想：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.

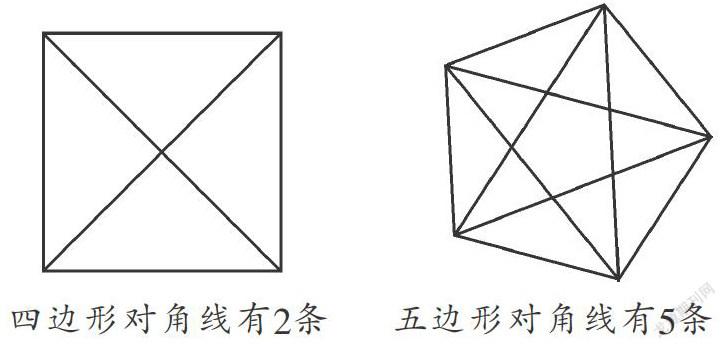
先考虑从一个顶点发出的对角线数目，它不能向本身引对角线，不能向相邻的两个顶点引对角线，它只能向n边形剩下的（n-3）个顶点连接对角线.因此，一个n边形从一个顶点能引的对角线数为n-3条；又因为n边形共有n个顶点，就一共能引n（n-3）条，但是考虑到每一条对角线都是由两个顶点连接构成的，这样计算所得的对角线中有一半是重复的，所以正确答案应该是 .

而多边形对角线的问题与另一个著名的问题有着异曲同工之妙，那就是“握手问题”.

“握手问题” 屋子里有n个人，每两个人都要握一次手，又不能重复握手，那么这n个人一共握了几次手？

我们可以把每个人看做多边形的顶点，每两个人握一次手就是每两个顶点之间连接一条线段.因不能和自己握手，所以一个人可以和n-1个人握手，所以总握手次数就是n（n-1）次；但你和我握与我和你握的意义是一样的，所以总次数中有一半是重复的，所以正确答案是 .

大家可以发现：多边形对角线问题与握手问题的本质是相同的.多边形对角线条数的解决其实是“握手问题”的一种应用.

握手问题除了能解决多边形条数问题外，还能解决送礼物问题：n个人，每两个人之间都要互送礼物一共要准备多少份礼物？握手问题中，我和你握手，你和我握手，属于重复，具有相同的意义；

送礼物问题中，我送你礼物，你送我礼物具有不同意义，不属于重复，所以可以得到n个人互相送礼物要送n（n-1）份.

类似，车票问题：一条刚开通的铁路上一共建设有x个车站，每两个车站之间要准备车票，那么要准备多少种车票？这个问题和送礼物问题同理，甲车站到乙车站的车票与乙车站到甲车站的车票意义不同，所以这条铁路x个车站之间一共要准备x（x-1）种车票.

看到这，大家有没有感受到数学问题很多都是相通的，关键就是识破它们各自的“伪装”.如果我们以后遇到一个较复杂的问题，我们可以试着像解决握手问题一样，先把它转换成一个我们所熟悉的问题，然后去探索两者之间的关系，这样去思考问题，复杂的数学问题有时候就不是一个难题了.

（指导老师：浦长宇）