探寻本质 多题归一
2015-09-10 09:07:07孙飞
初中生世界·七年级 2015年2期
孙飞
数学学习离不开解题.在解决问题时,我们可对问题的局部(条件或结论)进行改变(往往是位置或数量),从而得到新的数学问题.通过这样的改变,我们能够实现多题归一的目的,从而提升解决问题的能力.下以一例予以说明.
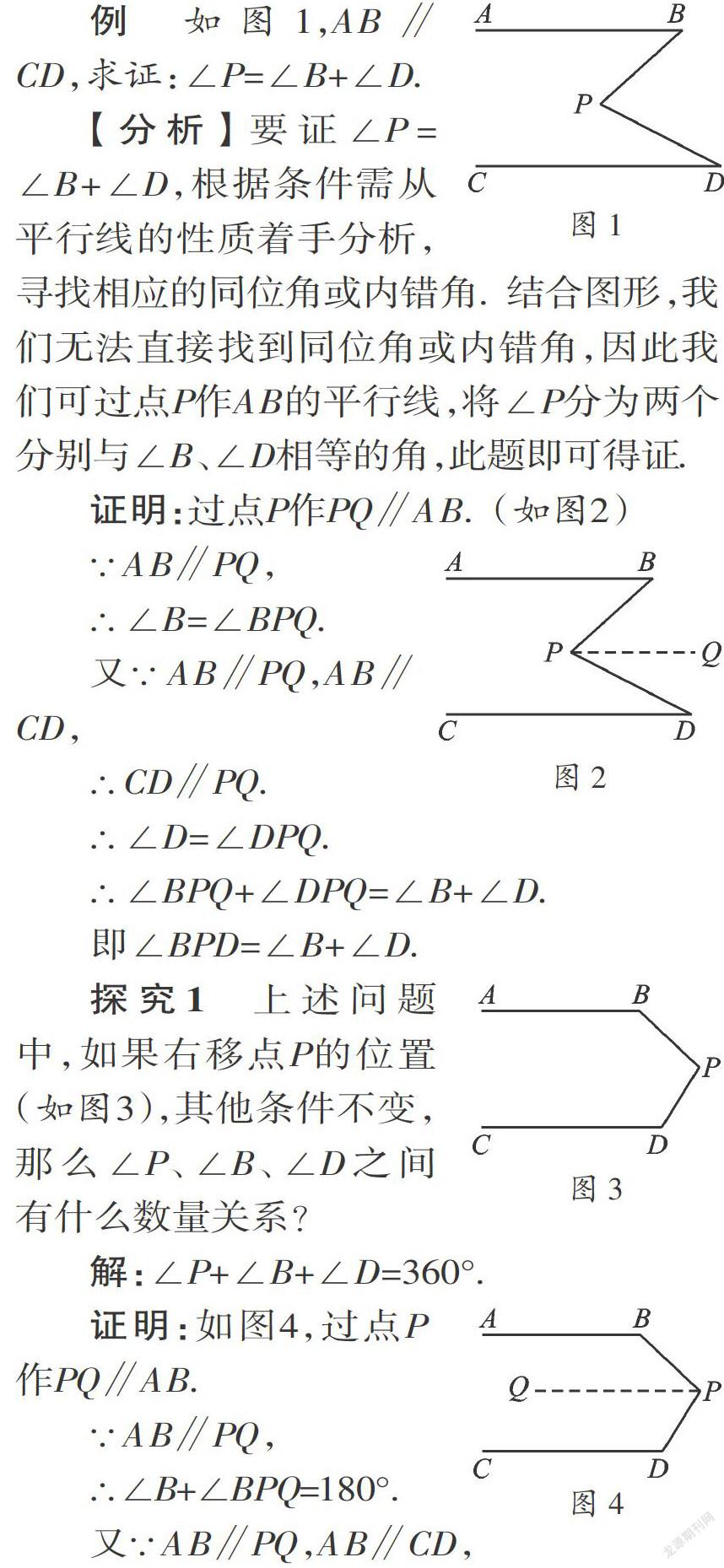
【分析】要证∠P=∠B+∠D,根据条件需从平行线的性质着手分析,寻找相应的同位角或内错角.结合图形我们无法直接找到同位角或内错角,因此我们可从点P作AB的平行线,将∠P分为两个分别与∠B、∠D相等的角,此题即可得证.
【分析】根据上述例子的解题方法,利用平行线的性质,不难推理出∠P=∠D-∠B,根据两直线平行,同位角相等;三角形外角的性质即可证之.
探究3 如果继续改变点P的位置(如图6),其它条件不变,那么∠P、∠B、∠D之间又有什么数量关系?
【分析】本题中没有已知的同位角(或内错角)可以利用,我们可根据上面积累的解题经验,作出合适的辅助线,构造出同位角(或内错角),从而解决问题.

探究4 如果将点P移到直线CD的下方,(如图8、图9),其它条件不变,那么∠P、∠B、∠D之间又有什么数量关系?
【分析】根据图8、图9,由上述的探究思路,不难得出以下结论.
如图8,有∠P=∠B-∠D.
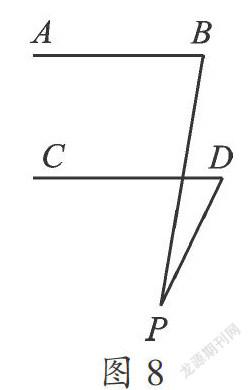
证明过程参见图5.
如图9,有∠P=∠D-∠B.
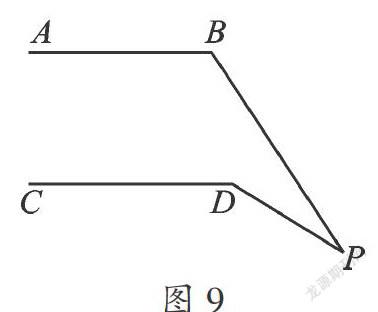
证明过程参见图6.
改变问题的局部只是给问题“换了件外衣”,其本质是并未改变.在平时的数学学习中,我们要善于在“变”中找出“不变”,洞察本质,从而实现问题的关联.
猜你喜欢
语数外学习·初中版(2022年1期)2022-05-30 21:26:23
故事作文·低年级(2021年4期)2021-05-06 03:11:13
中学生数理化·七年级数学人教版(2017年2期)2017-03-25 20:21:14
初中生世界·七年级(2017年1期)2017-01-20 20:46:43
中学生数理化·七年级数学人教版(2016年1期)2016-05-30 10:48:04
新课程·中旬(2009年16期)2009-10-27 10:53:26
中学生数理化·七年级数学华师大版(2008年11期)2008-12-23 08:33:48
中学生数理化·中考版(2008年4期)2008-08-23 10:03:30

