初中数学变式教学的优化探索

范丽娟

【摘要】在现在的初中数学课堂教学中，变式教学是一种常见而重要的教学方法.相应地，它能够对初中学生进行数学技能和发散思维方面的训练，进而培养初中学生分析问题和解决问题的能力.因此，本文作者对初中数学变式教学的优化探讨这个主题进行了相应的分析.

【关键词】初中数学；变式教学；优化；探讨

在经济转变和社会形势过渡的影響下，教育终将成为被关注的方向.纵观初中数学课堂，变式教学的应用便是教学模式在朝着更有利于教育发展方向迈进的重要见证.它的出现改变了传统数学课的教学模式，使教学方式更有利于学生的成长和学习，使初中学生从相应“变”的现象中去发现那些“不变”的本质.由于数学本身属于一门工具课程，不仅被广泛应用，而且具有这样的特点，理论多样，操作复杂.相应地，在初中数学教学中，相应的教学模式存在一定的问题，需要对它进行相应的优化，使它的优势得以更好地发挥.因此，本文作者对初中数学变式数学的优化进行了相应的分析，以此促进我国教育事业的发展.

一、数学变式教学的概述

总的来说，对于数学教学活动的实施，需要站在学生的角度，对课堂进行相应的设计和优化.相应地，变式教学这种新型的教学模式便是这样的一种教学模式.在数学教学中，变式教学是对相应的数学问题进行了不同角度、层次、背景、情形的变式.换句话说，变式教学是一种教学设计方法，它揭示了相应问题的本质特征，以此来展现不同知识之间的内在联系.相应地，具体地来说，所谓的变式教学就是指在教学中，站在一道母题的角度，对母题的问题、条件、设计的数学情景进行相应的改变，并进行重新探讨的一种教学方法.变式教学的核心便是利用构造一系列变式的方法，对相应的数学命题进行恰当的转化，来帮助学生透过现象去对数学的本质特征进行相应的了解.因此，在数学教学课堂中，相应的变式教学扮演着重要的角色.它不仅有利于学生对相应数学概念的理解，还能够对学生的思维进行相应的拓展，提高他们的学习兴趣，以此来使他们相应的能力得以提高.更重要的是，这种变式教学的教学模式能够让学生打破原有的思维定式，在变中求进，在进中求通，进行发散思维，来对相应的数学问题进行相应的分析和解决，进而帮助他们更好地去拓展相应的创新空间.

二、运用变式教学推进相应的数学教学

在数学教学中，相应的变式教学是它成长路上很好的助推器，帮助它在坎坷的路上更好地前行.首先，可以利用变式教学来促进数学知识的系统性.所谓的知识系统性主要体现在当下学生学习的知识方面以及前后逻辑的层次性.相应的变式教学可以让学生形成良好的数学知识结构，促进知识的系统性，对新课标下学生所遇到的数学问题进行很好的解决.其次，利用变式教学促进相应数学能力的发展.在变式教学中，它为学生提供了一个主动进行思维活动的环境.变式教学有利于提高学生的比较和概括能力.如在对“二元一次方程组的解法”进行相应学习的时候，把相应的课后习题和例题进行相应的融合，进而对相应的方程进行相应的变形.这样便让学生很清楚地认识到消元的关键是方程得变形.除此之外，变式教学能够消除学习定式的消极影响，有利于学生对知识更好地进行学习.最后，变式教学促进数学思维活动的质量.这主要是因为在变式教学中，学生能够从多层面、多角度来对相应的数学问题进行探讨，进而学生能够进行相应的创造性思维，相应地，数学思维活动的质量也得到一定程度的提高.

三、初中数学变式教学的优化探讨

在初中数学的课堂中，相应的变式教学并不是单一的.在相应的初中数学知识里，它对数学知识的很多方面进行了变式.比如，对相应结论的变式，对相应的解答过程的变式，对相应概念定义的变式，对定理公式的变式.因此，本文作者对初中数学的变式教学进行相应的分析，下面只是其中微小的一角.

1.初中数学中的条件变式法

在初中数学中，条件变式法是变式教学中很常见的，尤其是在对初中数学相应知识概念的教学.它有利于学生对相应数学知识的内涵进行全面的掌握，并进行灵活应用.所谓的条件变式法主要是指对题目问题的已知条件进行相应的改变，以此使相应的问题呈现出不同的形式，激起学生对此问题进行积极的思考，熟悉相应的题型变化.比如，条件变式法在这道初中数学题中的应用.它是一道对一元二次方程根的概念知识点进行相应考查的数学题.例：已知相应的方程x2-ax-3=0的一个根是2，那么a的取值是多少？相应方程还有一个根是多少？对于这道数学题，只需要用代入法就可以求出a的值，在此基础上，再去求解相应的方程，就可以知道还有一个根是多少.相应地，可以对此题进行相应的改变，引出相应的变式题.对于这道数学题，只需要把相应的常数项-3改为b.即已知方程x2-ax-3=0的一个根是b（b≠0），那么a+b的值是多少？虽然这道数学题的条件和问题有所变化，难度也有所增加，但它所考查的知识点仍然是关于一元二次方程的根.对于这道数学题，还可以进行进一步的变形.即如果b是方程x2-ax-3=0的根，那么b3-2b2-5b+1或者b2+1的值是多少？对于这道相关的变形数学题，可以利用根的定义，再结合等值变形的技巧就可以得出相应的答案.因此，从最初的那道数学题到引申出来的这些相关的数学题中，可以很清楚地知道，利用条件变式法对根的定义进行不同角度的运用，可以帮助学生对相应概念进行很好的掌握和理解.

2.初中数学中变结论的变式题

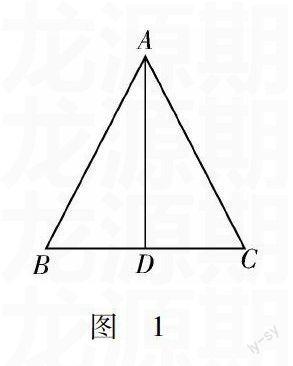
对于初中几何题，很多学生都是很畏惧的.这主要是因为几何数学题具有的难度.相应地，在初中几何数学中，运用变式教学的方式可以减少学生对几何的恐惧，提高他们对几何的学习兴趣.同时，它还能够对学生的思维定式进行克制，培养学生对具体问题进行灵活分析的能力，达到举一反三，触类旁通的效果.在初中几何中，变式教学主要是对原有的题目进行相应的图 1变形，比如，添加、改组、放大、颠倒.例如，△ABC是一个相应的钢架，AB=AC，AD是连接A和BC中点D的支架.求证：BD=CD.如图1所示.

对于这道几何数学题，可以利用“边边边”公理来进行相应的证明，进而可以对这道几何数学题进行相应的结论变式，进行相应知识的学习和掌握.例如下面四道与之相关的结论变式题：

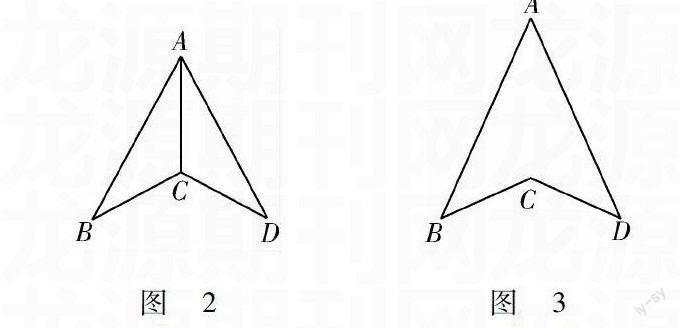
变式1：这道几何数学题的条件不变，求证：∠B=∠C.变式2：求证：AD⊥BC.变式3：已知，如图2所示，AB=AD，CB=CD，求证：△ABC≌△ADC.变式4：如图3所示，AB=AD，CB=CD，求证：∠B=∠C.

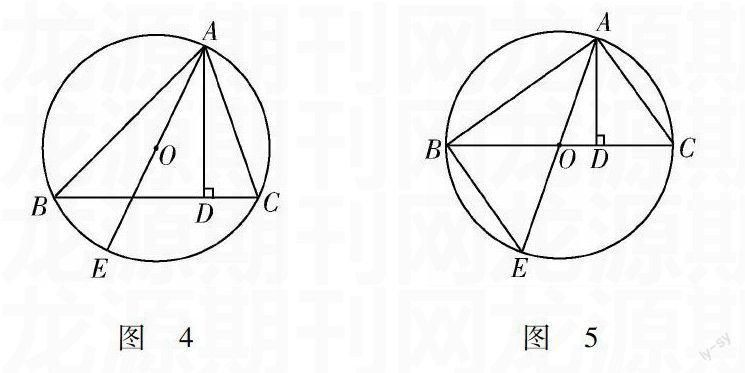
对于这四道引申出来的结论变式题，前面三道都属于相关的简单结论变式题，因此，很容易便可以得出相应的答案.但对于第四道相应的变结论的變式题，需要先构建相应的全等三角形，并再此基础上，添加相应的辅助线来连接AC，进而由相应的△ABC≌△ADC得出相应的结果.相应地，在几何数学中，相应问题的变化，将会致使相应的思路发生相应的变化.它也不仅仅是论证题，也会有相应的选择题和填空题出现.它不仅会帮助学生对相应知识点的理解和掌握，还能对他们解题的思路进行相应的改变.例如：如图4所示，AD是△ABC的高，AE是△ABC外接圆的直径，求证：AB·AC=AE·AD.

这道几何数学题主要是对相似三角形的性质进行相应的考查.对于这道几何数学题，通过对相应问题进行改变，可以变换成相应的选择题、填空题.例如：已知AD是△ABC的高，AE是△ABC外接圆的直径，连接BE.那么，图5中共有（ ）个三角形和△ABC相似.

由这道几何问题变式数学题得出，由原来的论证题变形为相应的填空题.很显然，在变式法下，相应的题型也发生了相应的变化.

总之，在初中数学教学中，变式教学是一种非常重要的教学方法.相应地，它不仅能使学生对初中数学的学习产生兴趣，还能提高他们相应的能力，培养他们的发散思维.因此，在初中数学教学中，需要把相应的变式教学放在至关重要的位置.最后，作者希望本文在给广大读者朋友们带去帮助的同时，也能引起他们对此新的认识和思考.

【参考文献】

[1]李忠芳.初中数学变式教学浅析[J].才智，2013（8）：122.

[2]宋遂青.变式法在初中数学教学中的应用[J].学周刊，2013（8）：177.

[3]周海燕.初中数学变式教学浅谈[J].中国校外教育，2013（32）：74.

[4]温河山.初中数学变式教学的方法探析[J].课程教学研究，2012，10：48-50+54.

[5]朱圣东.浅谈初中数学课堂变式教学的实践与策略研究[J].科技创新导报，2012（34）：187.

[6]杨丰采.有关初中数学教学中的变式教学分析[J].中国校外教育，2013（S2）：215.