初中数学教学中的“宏观微观说”
李百勉


摘 要:宏观元素,是指几何图形中的背景图形或概念中的主体;微观元素是指构成宏观图形的各个子图形——隐含在其中的基本图形或概念中的修饰语.在数学学习中,学生经常出现概念辨析不准、几何证明分析不出的情况,我们可以把原因归结为学生没有很好地把握数学概念和几何图形中的“宏观元素”和“微观元素”。将从代数概念教学的“宏观微观分析法”、挖掘几何图形中的宏观元素与微观元素、图形运动中的“宏观化”和“微观化”以及几何概念中的宏观元素与微观元素等方面例谈在初中数学教学中的探索与尝试。
关键词:概念教学;宏观元素;微观元素;几何图形
依照相对性原则,现实世界的客观事物都可以根据事物整体与局部的相对性,就其结构作出宏观与微观两个层次的划分.在数学学习中,学生经常出现概念辨析不准、几何证明分析不出的情况,这也一直是令每位教师困扰的问题.很多教师会说这是因为学生概念理解不透彻、思考问题不全面、综合分析能力差等原因,我把它归结为学生没有很好地把握数学概念和几何图形中的“宏观元素”和“微观元素”.
宏观元素,是指从几何图形中的背景图形或概念中的主体;微观元素是指构成宏观图形的各个子图形——隐含在其中的基本图形或概念中的修饰语.如果学生解题时善于从这两方面进行分析,解题的效率一定会有所提高.
一、代数概念教学的“宏观微观分析法”
数学概念(mathematical concepts):是指人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式,即一种数学的思维形式.正确地理解和形成一个数学概念,必须明确这个数学概念的内涵——对象的“质”的特征(宏观元素)及其外延——对象的“量”的范围(微观元素).“宏观与微观”分析法在数学代数概念的教学中应用比较多.
【举例】下列方程中,一元高次方程是( )
解析:B、C选项应该首先排除掉,因为这两个方程根本不具备宏观元素——整式方程,而A、D选项已经具备宏观元素,但还要由微观元素——含有未知数的项的最高次数大于2来衡量,因此,应该选D.
二、几何图形中的宏观元素与微观元素
初中数学中,几何证明是难点,很多学生不知从何入手,找不到解题的策略与方法,学生在学习几何的过程中,迫切想要知道的就是几何问题思考方法、分析方法的规律性,最迫切地想要知道的就是几何问题中添加的每一条辅助线是怎样想出来的.教师该如何帮助学生分析问题,找到解题策略显得尤为重要.实际上,解题时善于找出几何图形中的宏观元素和微观元素,会给解题带来事半功倍的效果.
【教学片段】(外出教研活动的素材)
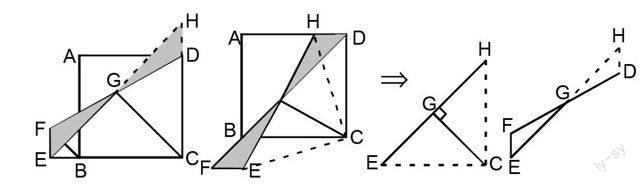
题目:如图,正方形ABCD的边AB上任取一点E,作EF⊥AB于点F,取FD的中点G,联结EG、CG.
(1)如图2-1(1),求证:EG=CG且EG⊥CG
(2)将△BEF绕点B逆时针旋转90°,如图2-1(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(3)将△BEF绕点B逆时针旋转180°,如图2-1(3),则线段EG和CG有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
生:自主思考问题,寻求解题思路.(能够填出辅助线的学生为数不多)
师:(师生共同分析)本题是以正方形为背景的几何证明题,我们应该知道正方形的性质,如,四条边都相等、对边平行、四个角都为直角、对角线相等且互相垂直平分、每一条对角线平分一组对角.从而得出∠EBF=∠EFB=45°.要证明“EG=CG且EG⊥CG”,则在本题的背景下应该考虑到证“全等”.由于本题中没有这两条边所在的全等三角形,所以,要“构造全等三角形”——过点G作GM⊥AB于点M,并延长MG交DC于点N(为了构造△GME与△CNG全等),同时,也出现了“一线三等角”的基本图形,如图2-1(4)结合点G为DF的中点,容易证出AM=ME=DN=GN,从而得证.
师:讲解了将△GFE绕点G顺时针旋转90°的方法,如图2-1(5)
对于这位教师的分析,我觉得可以充分肯定两点:①利用了几何图形的宏观元素——正方形,构造出图形中的微观元素——②解题的切入点是从要证的结论入手.这都是几何证明中的常用思路和方法.但是,我个人觉得本题的微观元素不止这些,还有点G为DF的中点(即DG=GF)和EF∥AD,如果这样的两个隐性元素结合在一起,我们自然会想到利用中心对称构造三角形全等,即“X型全等”,如图2-1(4)和2-1(5).同時,也引发出下一个基本图形——等腰三角形的“三线合一图”也就挖掘出两个基本图形.这样的解题学生更容易接受,也起到了多题一解的效果,学生更容易掌握图形运动的“不变形”,也就充分体现了数学教学中的通性通法.
因此,在几何证明中,我比较提倡在“宏观的背景下,从微观元素寻求解题方法”.这就要求教师和学生对微观元素的组合比较熟悉.以上两个基本图形,应用比较广泛.如,三角形中位线、梯形中位线的证明.
三、图形运动中的“宏观化”和“微观化”
学生学习几何,最怕图形中有动点或“背景图形”——宏观元素变换,经常出现束手无策的情况.这就要求教师在教学中要有机地变换宏观元素与微观元素,抓住一个“点”将其放大到“面”,即把微观元素“宏观”化(图形中的特殊元素更加一般化),将宏观元素“微观”化(减少背景图的特殊性),由研究一个问题,变成研究一类问题.
在教学片段1中,如果将教师所构造的微观元素——一线三角图进行放大,将上图中的微观元素——“△BEF绕点B旋转90°和180°”放大到“绕点B旋转任意角度”,G为DF中点,如图3-1(1),结论仍然成立.
【举例】如图3-3(1),已知在矩形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,
(1)求证:GF=GC.
(2)类比探究,如图3-3(2),将第(1)问中的矩形ABCD改为平行四边形,其他条件不变,(1)中的结论是否仍然成立?请说明理由.
本题中,第(2)问,实际是将(1)中宏观元素“矩形ABCD”微化到“平行四边形ABCD”,微观元素“Rt△GEF≌Rt△GEC(H.L)”宏化到一般三角形,由“∠B=∠AFE=∠GFE=90°”宏化到“非直角”.因此,由图形3-3(1)变到3-3(2),通过证明三角形全等来证明等线段的方法行不通(因为“边边角”不一定全等).但是本源性的元素“BE=EF=EC”和“∠GFE=∠GCE(等角的补角相等)”不变,结论“GF=FC仍然成立,诸如此类的题目有很多.
四、几何概念中的宏观元素与微观元素
宏观与微观是相对的、辩证的.在数学教学中,我们教师都应该不断地探索宏观元素“微”化,微观元素“宏”化来研究问题.在初中数学领域,不止在代数概念、几何图形分析证明中存在“宏观微观说”,在几何概念辨析的教学中也实用,如,在四边形的教学中,在宏观元素——四边形的基础上,添加一个微观元素,如,“对角线互相平分”或“一组对边平行且相等”或“两组对边分别平行”等,就可以得出该四边形为平行四边形.
又如,在宏观元素——平行四边形的基础上,添加一个微观元素——对角线相等,则会得出该四边形为矩形,即对角线相等的平行四边形是矩形.如果再将这里的宏观元素——“平行四邊形”微化成“四边形”,结论仍然成立,那么微观元素——“对角线相等”则要继续“微”化,变成“对角线互相平分且相等”.因此,在几何概念教学中,存在宏观“宏”,微观“微”的说法.
如果把一堂课的总体达成度看成“宏观”元素,那么学生的个性发言则是起主导作用的“微观”元素.教师在批改作业时,要关注学生的“微观”个体,讲评作业时,则要关注的是学生的“宏观”问题,即主要问题.图形运动有规律,动中不变很常见;透过宏观看微观,放大微观成宏观;微观结合不一般,基本图形在里边.通过“宏观”看问题,分析微观寻策略.只有在教学中不断探索和研究,课堂才会有效,学生的数学学习才会更加得法.
参考文献:
[1]颜庭飞.浅谈对初中数学概念教学的技巧[J].数学学习与研究,2011(04).
[2]林东平.引导学生正确寻找解题思路的探索[J].中学教学参考,2012(10).
编辑 郑 淼

