机械振打除灰装置的纵向冲击特性
靖 静, 喻九阳, 郑小涛, 林 纬, 王成刚
(武汉工程大学 机电学院,武汉 430073)
由武汉工程大学自主研发的“机械振打器”已在湖北双环、广西柳化、河南开祥等国内十几家煤气化企业成功应用。机械振打器安装在煤气化炉水冷壁上并通过敲击水冷壁而起到除灰的作用,且机械振打器的冲击性能特别是撞击杆两端面上的应力和速度直接影响装置的除灰效果和使用寿命。本文通过研究机械振打器的冲击特性,以期进一步提高机械振打器的工作效能。
结构的弹性冲击是一个经典的问题,在工程实践中有重要的应用背景。诸德超等[1]将弹性碰撞问题纳入振动分析过程,使用已成熟的振动响应分析方法及程序,避免了时序法选择补偿的繁琐过程。张继业等[2]研究了具有一般边界条件的杆在刚体纵向冲击下的振动问题。吴家强等[3]用模态法分析了任意支撑条件下杆的冲击动力响应。李敏[4]等将含大参数的二阶线性方程的修正摄动解应用于楔形杆轴的固有纵振和扭振的研究。邢誉峰[5]给出了一种考虑非线性HERTZ弹性接触变形的线性化方法和计算步骤。关于机械振打器这种具有特殊边界条件的杆冲击问题,尚鲜有报道。因此,本文对机械振打器的冲击过程进行了系统的理论分析,以期为机械振打器的设计和优化提供理论支持。
1 机械振打器的冲击模型
活塞杆与撞击杆的纵向撞击过程如图1所示,撞击杆长l,横截面积A,质量密度ρ,弹性模量E,撞击杆左端弹簧和右边弹簧的弹性系数分别为k1和k2,其中k1,k2≠0,右边弹簧预压缩量为l0。本文忽略撞击杆的重力和材料阻尼,将活塞杆视为质量为m的质量块。以撞击杆最左端的位置为原点建立坐标系。
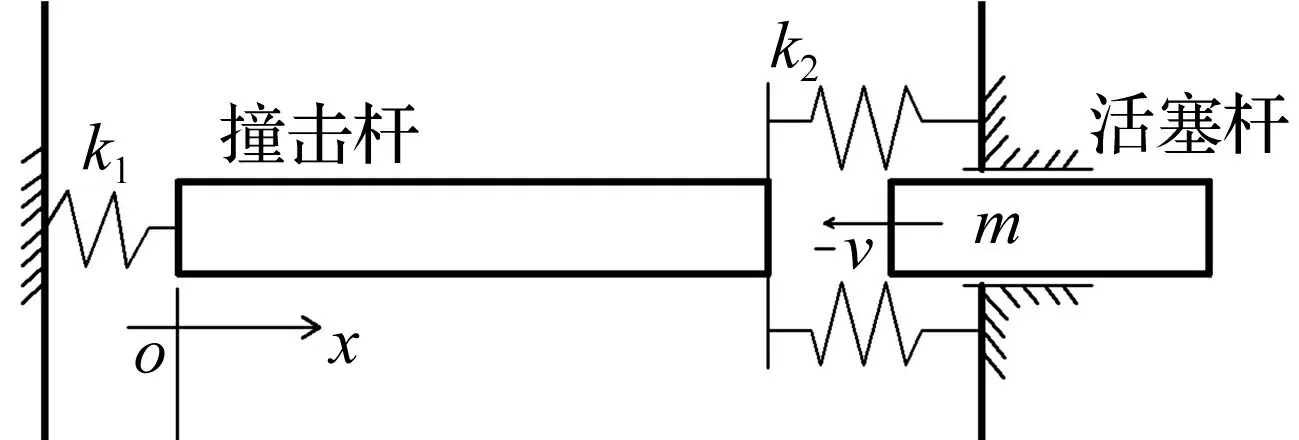
图1 振打器冲击部分简化模型
由以上模型及Timoshenko等[6]建立活塞杆和撞击杆纵向碰撞的控制方程:
(1)
碰撞后的边界条件为:
(2)
(3)
式(2)和式(3)分别为撞击杆左右两端力的平衡方程。
活塞杆与撞击杆碰撞时的位移和速度初始条件为:
u(x,0)=0 (0≤x≤l)
(4)
(5)
(6)
在活塞杆与撞击杆初始碰撞的瞬间,仅在撞击杆x=l处的微元受到撞击而具有速度,其他部分均处于静止状态,且冲击波在杆内以速度c沿x轴负方向传播,而波未到达的杆内微元处于静止状态。
2 模型的解
波动方程(1)的一般解的形式为:
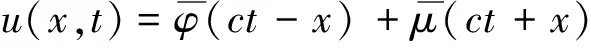
(7)
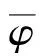
由式(7)可得:
(8)
(9)
由位移初始条件式(5)得:
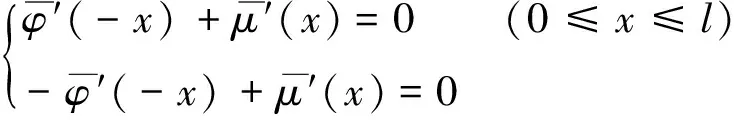
(10)
令z=x,带入式(10)得:

(11)
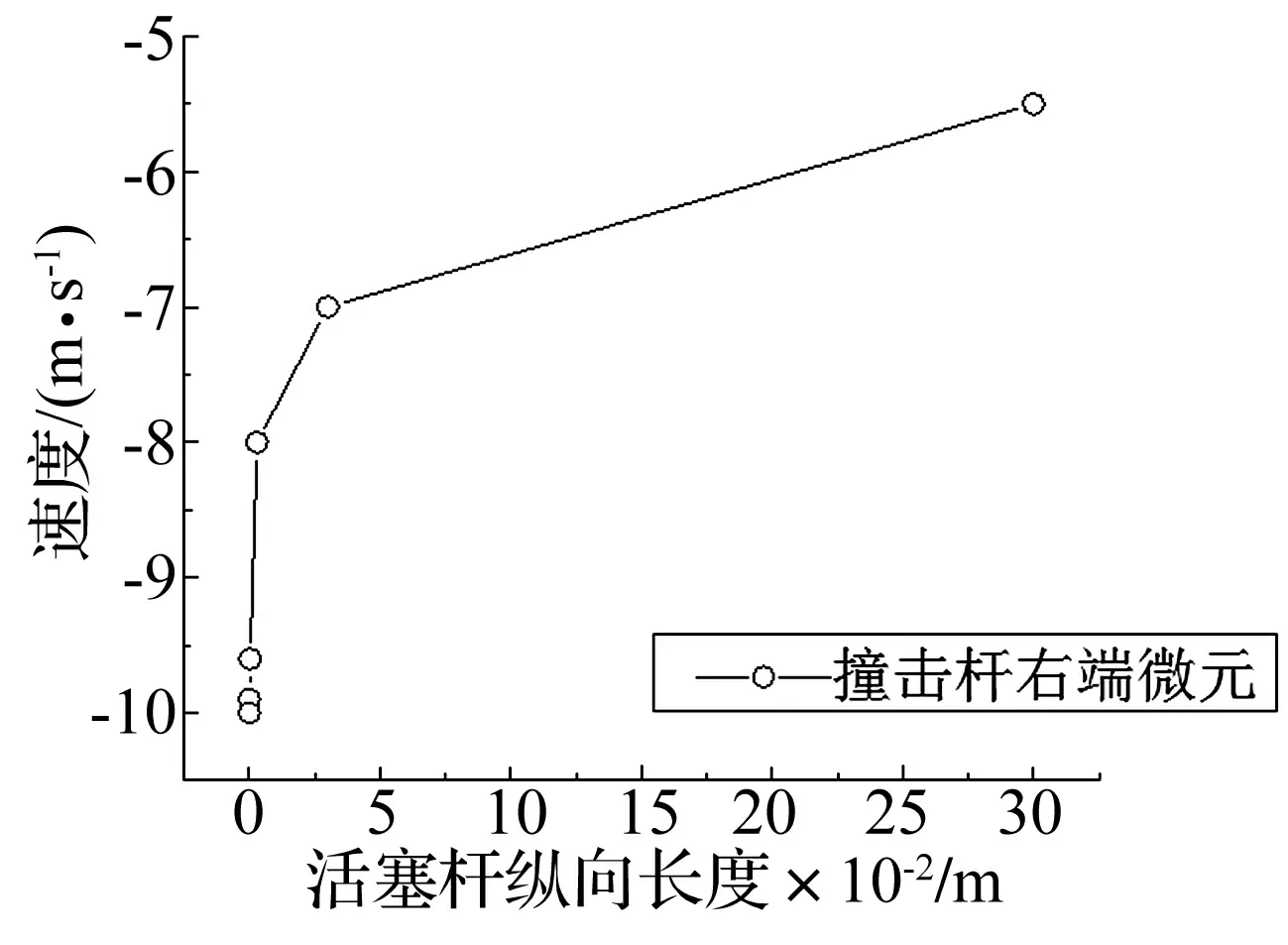
由式(5),(7),式(11)可知,在(0≤x (12) 令 (13) 则: (14) 由边界条件(2)可知,对任意ct有: μ′(z)+β1μ(z)+β2l0=φ′(z)-β1φ(z) (z≥0) (15) 由式(14)知,β1φ(z)=φ′(z)-β2l0(0≤z 则 φ(z)=Feβ1z-Fφ′(z)=Fβ1eβ1z (0≤z (16) 令m=λAρl,z=ct+l,并将式(7)代入式(3)得: (z≥l) (17) 当l≤z≤2l时,有-l≤z-2l≤0,由式(14)得,φ″(z-2l)=φ′(z-2l)=0,则式(17)可变为: (18) 将式(18)看作关于μ(z)的二阶常系数非齐次线性微分方程,根据u(x,t)在点(l,0)关于时间连续,得: μ(z)=C1eWz+C2eXz-l0 (l≤z<2l) (19) μ′(z)=C1WeWz+C2XeXz (l≤z<2l) (20) 其中, 将式(19)和式(20)代入式(15)可得: (l≤z<2l) (21) 其中,C5=Reβ1l-F。 当2l≤z<3l时,有0≤z-2l (22) 其中: (2l≤z<3l) (23) (2l≤z<3l) (24) 其中: 将式(23)和(24)代入式(15)可得: (25) 且 根据活塞杆与撞击杆的碰撞情况,如果两杆在0≤t<2l/c时间内没有分离,则需要将μ(z)在z>3l上拓展。判断各时间下x=l面的应力情况,当0≤t<2l/c时,σ=E∂u(l,t)/∂x<0,活塞杆对撞击杆是压应力,当t=(2l/c)+时,σ=E∂u(l,t)/∂x>0,则活塞杆对撞击杆是拉应力。所以活塞杆和撞击杆在t=2l/c时分离,无需将μ(z)在z>3l上拓展,即活塞杆与撞击杆的冲击时间是2l/c。文献[7]对刚体与自由杆冲击进行了数值计算,所得冲击时间与上面结论一致。 从两杆接触开始到分离结束,撞击杆各点的位移,应力和速度分布分别为: (1) 当-l φ(ct-x)+μ(ct+x)=0 (2)当0 u(x,t)=φ(ct-x)+μ(ct+x)=Feβ1(ct-x)-F (3) 当l≤ct-x<2l,0≤ct+x (4) 当2l≤ct-x<3l,0≤ct+x (5) 当-l≤ct-x≤0,1≤ct+x<2l时,由式(14),式(19)和式(20)得: u(x,t)=0+μ(ct+x)=C1eW(ct+x)+C2eX(ct+x)-l0 (6) 当0 u(x,t)=Feβ1(ct-x)-F+C1eW(ct+x)+C2eX(ct+x)-l0 σ=-Eβ1Feβ1(ct-x)+E[C1WeW(ct+x)+C2XeX(ct+x)] V=cβ1Feβ1(ct-x)+c[C1WeW(ct+x)+C2XeX(ct+x)] (7) 当l≤ct-x<2l,l≤ct+x<2l时,由式(21),式(19)和式(20)得: +C1eW(ct+x)+C2eX(ct+x)-l0 (8) 当2l≤ct-x<3l,l≤ct+x<2l时,由式(25),式(19),式(20)得: -C6)eβ1(ct-x-l)]+E[C1WeW(ct+x)+C2XeX(ct+x)] (9) 当-l (10) 当0 (11) 当l≤ct-x<2l,2l≤ct+x<3l时,由式(21),式(23),式(24)得: (12) 当2l≤ct-x<3l,2l≤ct+x<3l时,由式(25),式(23),式(24)得: 以机械振打器实际工况为例,各参数如表1所示。 表1 振打器参数表 这里采用ansys/ls-dyna进行模拟计算如图2。其中,弹簧k1为1个COMBI165单元,含2个节点,左端节点受全约束;弹簧k2为两个COMBI165单元,含4个节点,右端两个节点受全约束;撞击杆为2 264个SOLID164单元,含3 010个节点;活塞杆为810个SOLID164单元,含1 072个节点,其冲击速度为10 m/s。 图2 振打器冲击部分有限元模型 由于活塞杆被视为质量块,即体积趋近于零,密度极大。因此对于活塞杆的建模,其纵向长度会影响计算结果的准确性。给出不同活塞杆纵向长度下,撞击杆右端微元峰值速度变化的曲线如图3。 图3 撞击杆右端微元速度的变化 由上图可以看出:模型中活塞杆纵向长度越小,撞击杆右端微元峰值速度就越大,且最终趋近于-10 m/s。其中当活塞杆长度设定为0.000 2 m时,撞击杆右端微元峰值速度为-9.8 m/s,相对于-10 m/s偏差已经非常小,以下数据都基于该算例。 几个特殊时间和部位的应力、速度分布的有限元解与解析解的对比如图4~图9所示。 结果表明,撞击杆上的应力和速度分布符合工件的实际特征,验证了本文解析解的可靠性。值得注意的是:冲击波在传播过程中,受到材料阻尼等因素影响,幅值有所减少;图4~图9中撞击杆某处微元在某一时刻的应力和速度存在突变现象,此现象与速度初始条件式(5)和式(6)相吻合,原因在于应力波在传播到该处时,该处微元各质点在瞬时冲击作用下发生速度和应力的跳跃变化。 图4 t=l/2c时的应力分布图 图7 t=l/c时的速度分布图 本文建立了机械振打器活塞杆与撞击杆纵向冲击问题的理论模型,并推导了其特殊边界条件下的解析解,主要结论如下: (1) 基于波动方程建立了机械振打器活塞杆与撞击杆纵向冲击问题的理论模型。 (2) 推导了撞击杆冲击过程中位移、速度、应力以及两杆的冲击持续时间的解析表达式,并采用有限元方法验证了本文解析解的正确性。 参 考 文 献 [1]诸德超,刑誉峰.点弹性碰撞问题之解析解[J].力学学报,1996,28(1):99-103. ZHU De-chao, XING Yu-feng. Analytical solution of point elastic impact between strvctures[J].Actamechanicasinica, 1996,28(1):99-103. [2]张继业,曾 京,舒仲周. 杆的纵向冲击振动[J].振动与冲击,1999,18(3):57-61. ZHANG Ji-ye, ZENG Jing, SHU Zhong-zhou. Longitudinal vibration of prismatic bar during impact[J]. Journal of Vibration and Shock, 1999 ,18(3):57-61. [3]吴家强,王宏志. 杆的纵向冲击全过程分析[J]. 振动与冲击,2004,23(1):101-107. WU Jia-qiang, WANG Hong-zhi. General procedure for analysis of axial response of prismatic bar during impact[J]. Journal of Vibration and Shock, 2004,23(1):101-107. [4]李 敏,李 嘉.楔形杆轴纵、扭固有振动的修正摄动解[J].振动与冲击,2001,20(3):42-43. LI Min, LI Jia. The corrected perturbation solution of longitudinal and twist natural vibration of tapered axes[J].Journal of Vibration and Shock,2001,20(3) : 42-43. [5]邢誉峰,诸德超.两杆纵向非线性弹性碰撞的瞬间响应[J].北京航空航天大学学报,1998,24(1):39-42. XING Yu-feng,ZHU De-chao.Transient analysis of nonlinear elastic impact between two rods[J]. Journal of beijing university of aeronautics and astronautics,1998,24(1):39-42. [6]Timoshenko S.Vibration problerms in engineering[J].Third Education, 1955, 417-424. [7]邢誉峰,诸德超. 用模态法识别结构弹性冲击载荷的可行性[J]. 力学学报, 1995,2 (5) :560-566. XING Yu-feng, ZHU De-chao. The feasibility of the determination of rigid/elastic impact loads between structures with the method of mode superposition[J].Actamechanicasinica,1995,2(5):560-566.
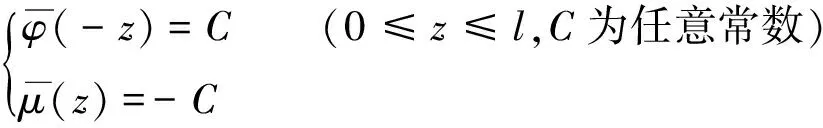

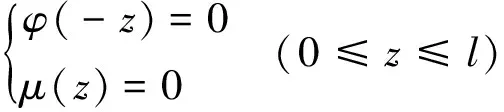



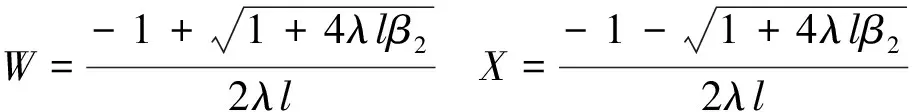

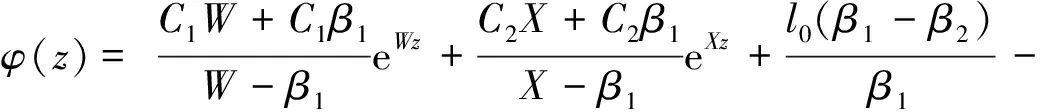
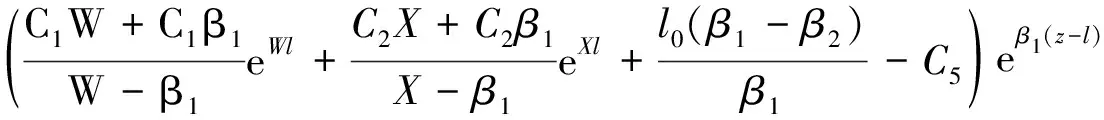


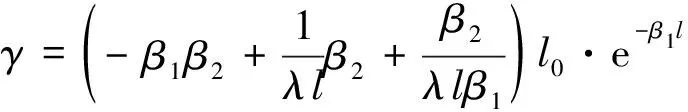


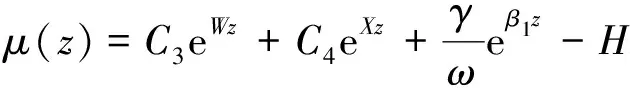
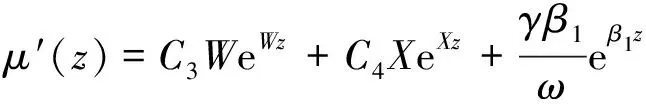
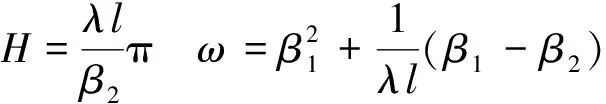
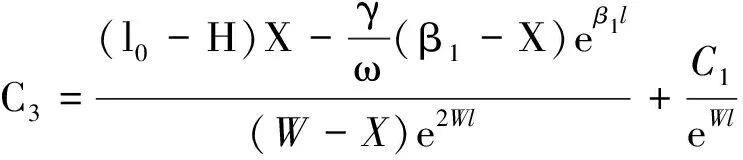





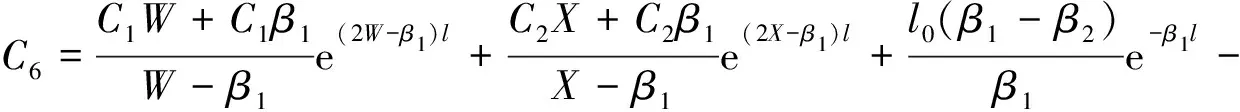
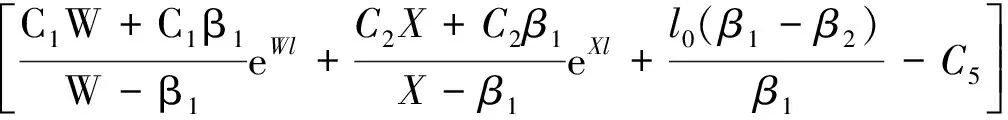
3 活塞杆与撞击杆的冲击时间
4 撞击杆各点的位移、应力和速度分布
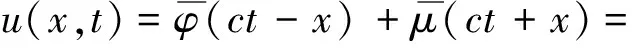

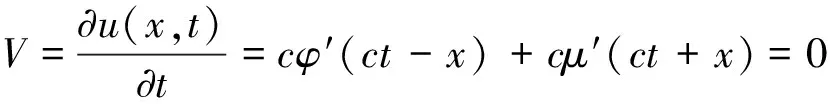

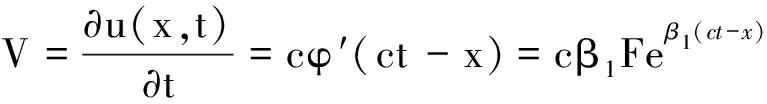
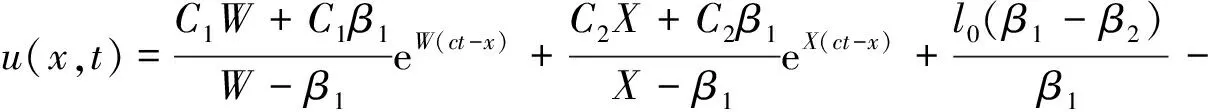


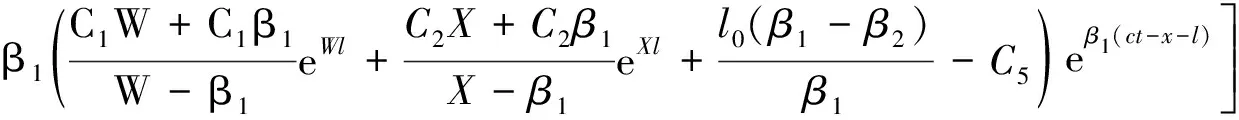

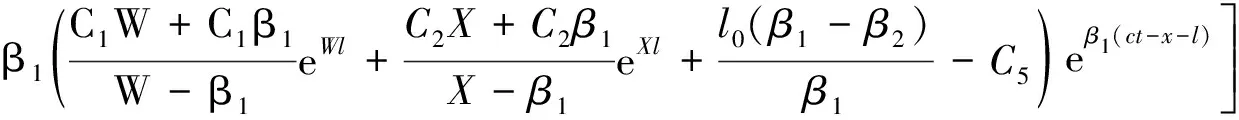
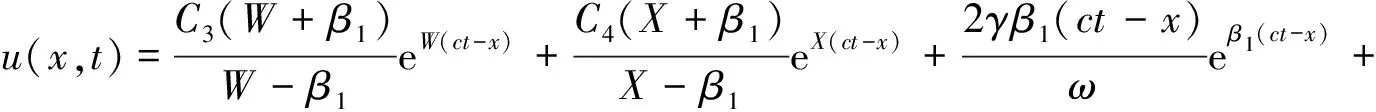
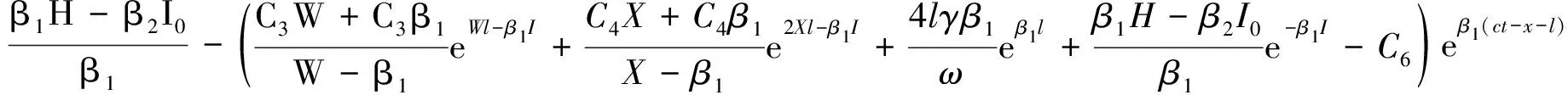
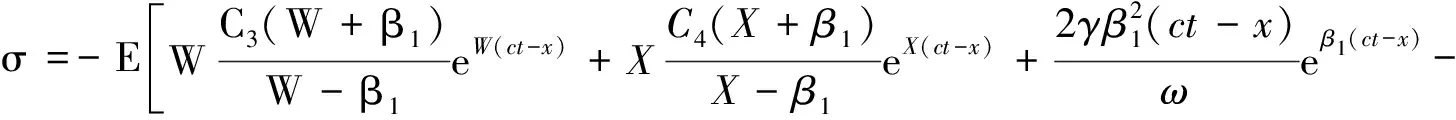
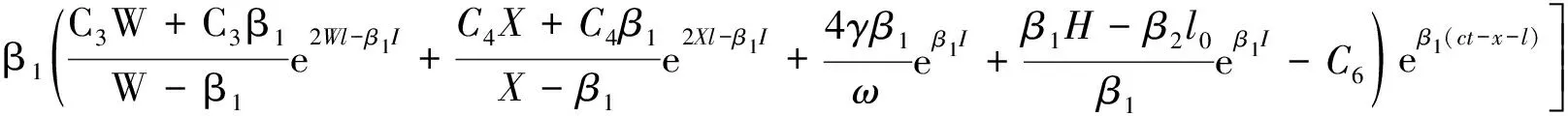

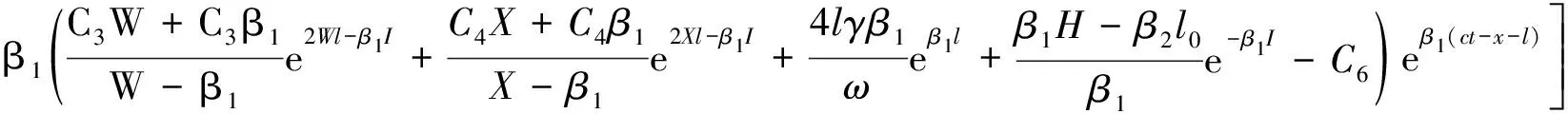


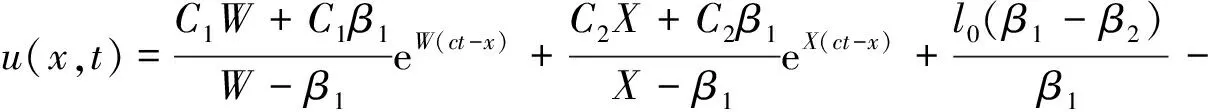





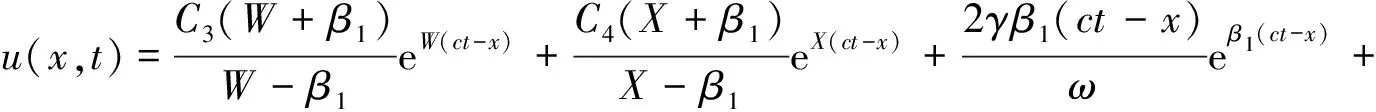


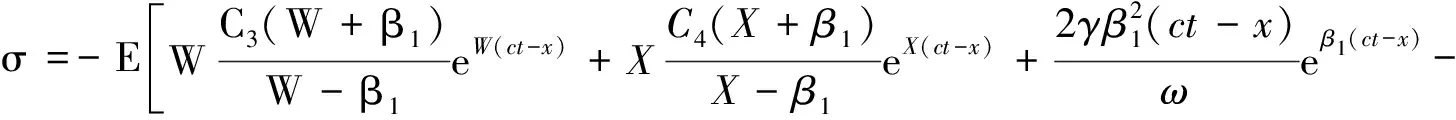
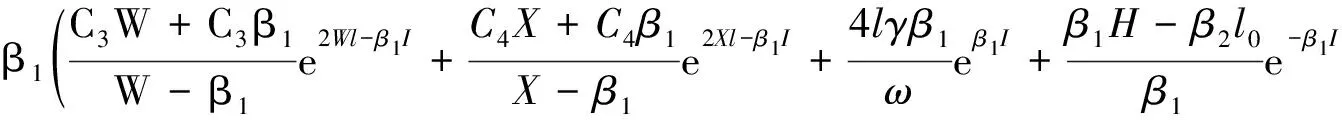
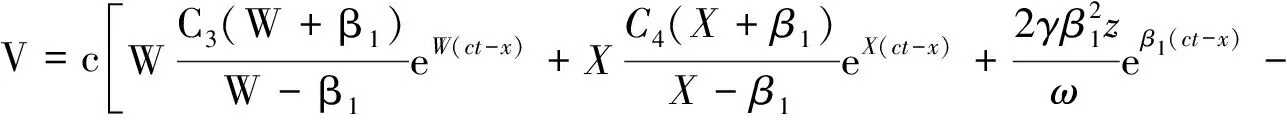

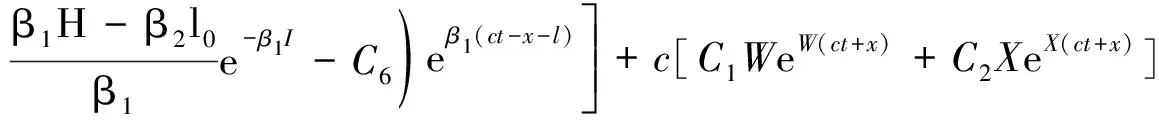
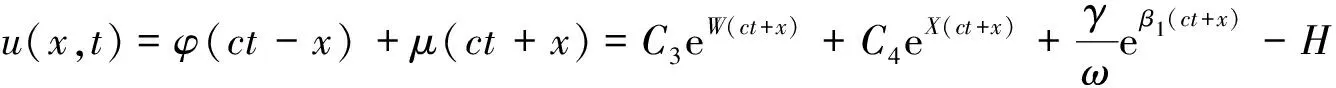

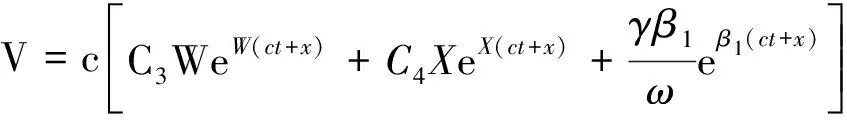



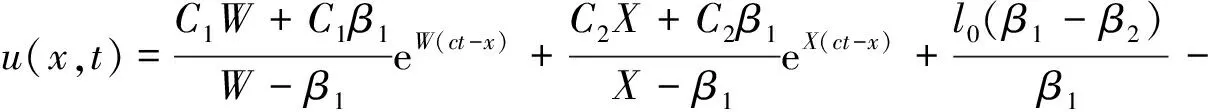




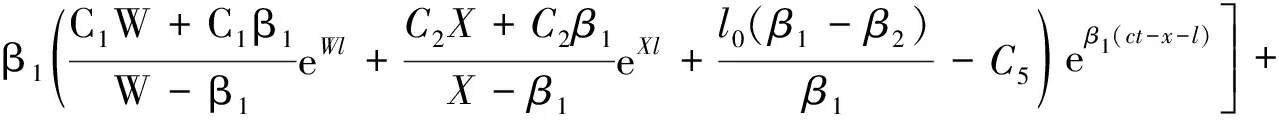

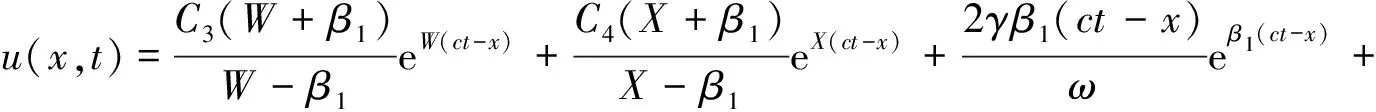


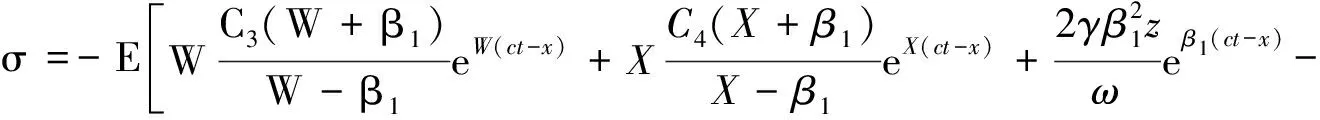


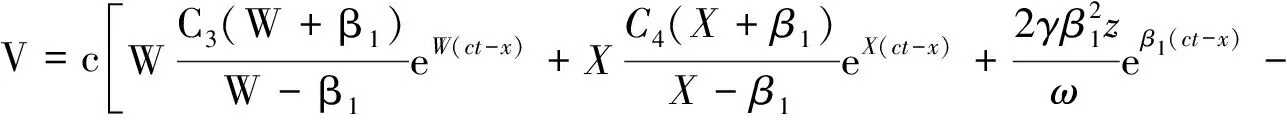

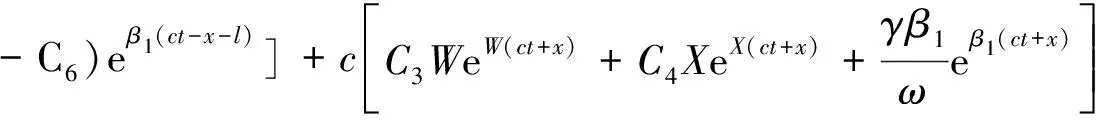
5 计算实例




6 结 论

