低速风洞模型振动主动控制仿真研究
王 学, 陈陆军, 黄 勇, 孔 鹏
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000;2.中国空气动力研究与发展中心低速所, 四川 绵阳 621000)
中国空气动力研究与发展中心4 m×3 m风洞是我国大型低速主力风洞,风洞配备的弯刀尾撑机构和大迎角尾撑机构均采用悬臂方式支撑模型,如图1和图2。在外载荷(重力和非定常气动力)作用下,悬臂支撑在前端通常产生较大的位移。在大迎角等气动分离较为剧烈的状态下,悬臂前端的模型产生大幅的振动[1]。风洞试验中,模型的振动首先危害到气动试验数据的精准度,这将对飞行器后续的工作产生深远的影响,甚至危及我军战斗力的生成。模型的振动严重时还危及试验设备和人员的安全,缩短设备使用寿命,造成系统故障率上升[2]。

图1 4 m×3 m风洞弯刀尾撑系统
风洞模型振动控制分为主动和被动两种方法。国内风洞在振动主动和被动控制方面均进行了探索研究[2-4]。风洞试验的试验对象各异、试验状态多样,造成风洞试验中模型振动特性各异。因此,适应性较强的主动控制越来越受到风洞振动控制研究者的关注,国外ETW风洞和NASA风洞均研究了模型的主动抑振[5-6],获得了较好的效果。
本文针对4 m×3 m风洞开展模型振动主动控制技术研究,提出了相应的主动抑制方案,并对各主动控制方案进行了有限元方法(FEM)动力学仿真分析。第1节对低速风洞尾撑装置进行了有限元(FE)建模,进而分析了尾撑装置的动力学特性。第2节针对4 m×3 m风洞尾撑置装提出了振动的主动控制方法。第3节给出了尾撑装置振动主动控制FEM仿真方法,以及控制力的光滑预测方法。第4节对FEM仿真计算结果进行了对比及分析。第5节给出了4 m×3 m风洞尾撑装置振动主动控制FEM仿真结论。

图2 4 m×3 m风洞大迎角尾撑系统
1 低速风洞尾撑装置FEM分析
1.1 FEM建模
为便于仿真计算,在不影响结构主要动力学特征的条件下,对4 m×3 m风洞尾撑装置进行了FEM简化。简化后采用ANSYS软件建立4 m×3 m风洞尾撑装置FEM模型,采用四面体进行网格划分,在各连接界面进行网格加密处理。计算网格节点数为10.1万,单元数为5.2万,计算网格和坐标系如图3所示。
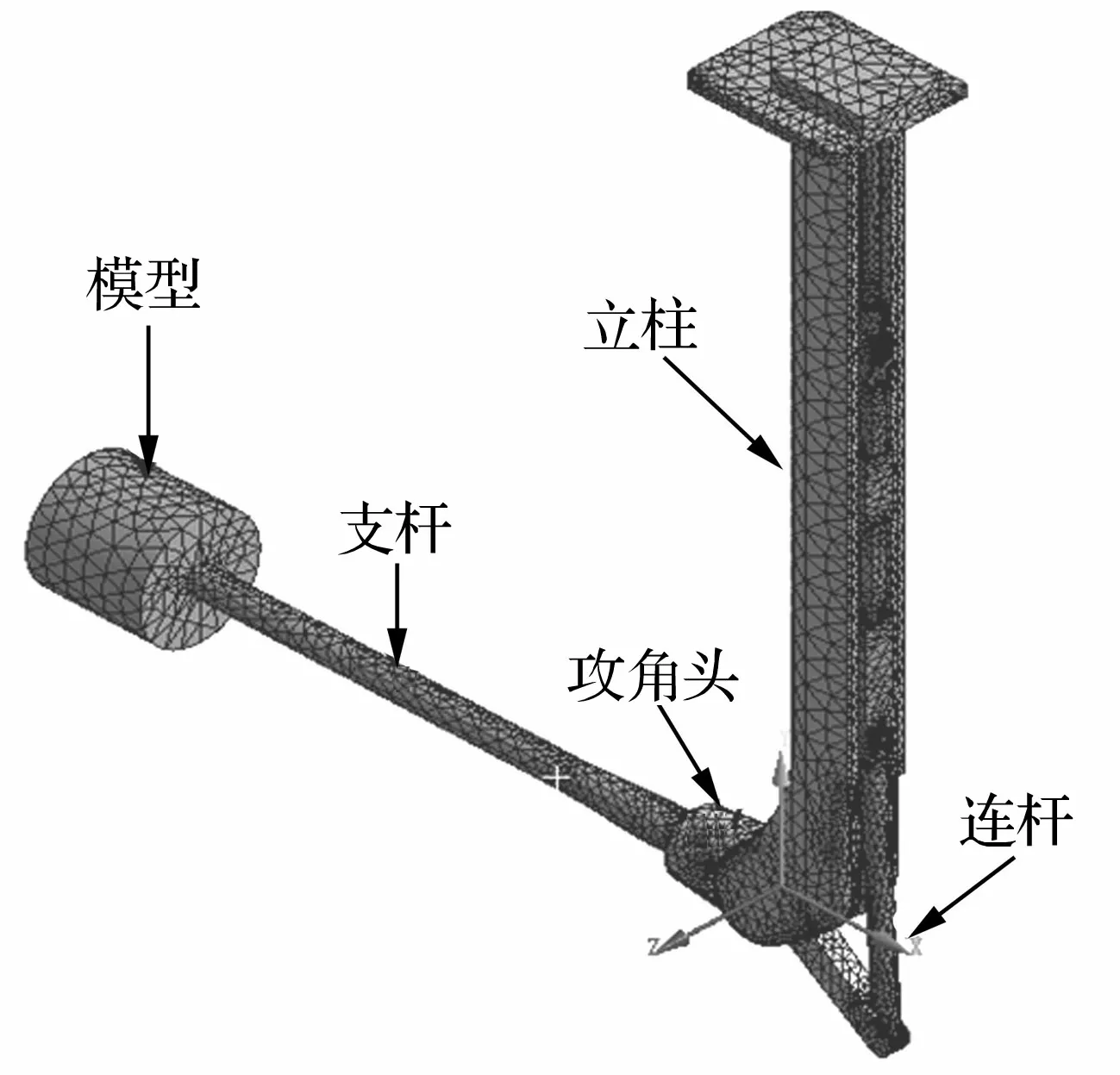
图3 4 m×3 m风洞尾撑装置FEM模型
1.2 模态分析
模态分析结果如表1和图4所示,一阶模态为模型和尾支杆的横向运动,二阶模态为模型和尾支杆的俯仰运动,三阶模态为模型、尾支杆和大臂的横向运动。

表1 4 m×3 m风洞尾撑装置固有频率

图4 4 m×3 m风洞尾撑装置各阶振型
1.3 瞬态动力学分析
基于1.2节的模态分析结果,采用模态叠加法,对未施加振动控制措施的尾撑装置进行了瞬态动力学分析。气动载荷采用某型典型战机风洞试验获得的天平载荷数据,如图5所示。计算时间步长取为Δt=1.0×10-3s。模型前端点Y向位移时间历程如图10和图13中黑细实线所示。

图5 气动载荷
2 尾撑装置振动主动控制方案
2.1 振动主动控制原理
振动主动控制方法原理是,传感器实时采集的结构响应或环境干扰量,控制器采用一定的控制算法计算出所需的控制力,执行机构(作动器)将控制力施加于结构上,如此循环以达到振动控制的效果[7]。施加了主动控制力的结构动力学FE方程如下:
(1)

(2)
式中,ξ、λ和κ分别为位移、速度和加速度反馈控制参数。对比式(1)和式(2)可知,控制力fctr等效于改变原结构的质量矩阵、阻尼矩阵和刚度矩阵,以达到改变结构动力学响应特性、消耗振动能量,最终实现振动控制的效果。
2.2 尾撑装置振动主动控制方案
针对4 m×3 m风洞尾撑装置特点,可采用天平信号或加速度计信号作为信号反馈,采用压电陶瓷堆作为执行机构核心部件。主动控制作用点的选择有两种方案:支杆前端控制和支杆后端控制。支杆前端/后端控制是在支杆靠近模型/立柱一端绕支杆布置数量不等的压电陶瓷堆施加控制力。支杆后端控制方案压电陶瓷堆安装方式如图6所示,支杆前端控制方案与此类似,控制方案的原理如图7所示。根据图6和图7,尾撑装置振动的主动控制原理是通过传感器采集并反馈模型的振动信号,控制模块据此计算并输出控制命令,控制点安装的压电陶瓷根据控制命令输出控制力(亦即控制弯矩),以此循环往复,以达到抑制模型振动的目的。

图6 压电陶瓷堆安装示意图

图7 风洞尾撑装置主动控制原理图
3 尾撑装置振动主动控制FEM仿真
3.1 FEM仿真方法
为了进行尾撑装置振动主动控制FEM仿真,在控制点处支杆上下表面分别施加大小相等、方向相反的集中力,从而等效于在控制点施加了一个主动力矩,以此模拟压电陶瓷堆的作用力,如图8所示。仿真过程中,控制力随反馈的结构响应实时变化。为了便于对比分析,本文在仿真过程采用线性主动控制,即主动控制力随反馈信号线性变化,而控制参数ξ、λ和κ不随时间变化。

图8 主动控制FEM仿真示意图
根据结构动力学原理,位移反馈和加速度反馈控制力等效于移动了结构的固有频率,对于窄频外载荷较为有效。在风洞试验中,气动载荷通常为宽频载荷,因此在仿真中仅使用了速度反馈控制力,即:
(3)
在FEM仿真中,上一时间步的结构响应计算结果作为当前时间步控制力的计算依据。本文基于ANSYS APDL编程语言进行有限元仿真,在瞬态动力计算中采用模态叠加法。在ANSYS中采用模态叠加法时,求解过程输出的计算结果只包括模态参数,为了提取节点速度需在每个时间步求解完成后调用后处理程序,然后采用“重新启动”模式进行计算。本文采用的APDL程序流程如图9所示,图9 中虚线方框内为相应模块使用的主要APDL命令。
3.2 主动控制力的平滑预测方法
在主动控制有限元仿真计算中,结构响应反馈信号中通常包含高频信号,直接据此生成控制力,控制效果较差,严重时会导致高频振动的发散。为此,需要对主动控制力进行平滑处理,本文采用的方案是:提取当前时刻tn之前的n步计算结果进行线性平滑处理[8],然后预测下一时刻tn+Δt的结构响应变量,并据此计算主动控制力。

图9 APDL程序流程
令在tn之前n个时间步t1,t2,…,tn的结构响应值为y1,y2,…,yn。线性平滑处理即为选取参数a,b使得各点关于直线方程:
y=a+bt
(4)
的误差平方和最小,亦即:
(5)
从而获得关于参数a,b的方程组:
(6)
解得:
(7)
其中,


(8)
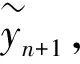
(9)

4 FEM仿真计算结果及分析
根据第2节提出的主动控制方案和第3节给出的FEM仿真方法,分别对支杆前端和后端控制进行了FEM瞬态动力学仿真分析。仿真过程中主动控制力随结构响应实时反馈,控制力按式(3)进行计算,与结构响应呈线性关系。
4.1 支杆后端控制方案FEM仿真
对于支杆后端控制方案,分别对控制参数λ=0.2,0.35,0.5,0.8,1.0,1.5,2.0等情形进行了FEM瞬态动力学仿真分析。图10给出了λ=0.35和λ=2.0时模型前端点的y向振动位移时间历程,图11和图12分别对各控制参数条件下y向振动位移、控制力的时间历程进行了对比。从上述计算结果可以看到,该支杆后端控制方案能够有效抑制结构的振动。随着控制参数λ的增大,结构低频振动衰减加快,同时控制力峰值亦显著增大。

图10 后端控制方案位移时间历程
由图10和图11可知,当λ≥0.35时,随着λ的增大,结构高频振动(三阶模态)被逐渐激发;当λ>1.0时,高频振动趋于发散,振动恶化。从图12可知,随着高频振动发散,控制力亦趋于发散。造成该现象的原因分析:支杆后端控制方案的控制点位于整个尾撑装置中间部位,根据1.2节模态分析结果,此处的振动主要受到高阶振型的影响,因此在此处施加的控制载荷也易于激发高频模态响应。可见,支杆后端控制方案需选择恰当的速度反馈控制参数,即在振幅较大时可选用较大的速度反馈控制参数,而当振幅大幅衰减后应选用较小的速度控制参数,以免激发高频振动。

图11 后端控制方案不同控制参数位移对比

图12 后端控制方案控制力时间历程
根据仿真计算结果,控制参数λ=0.2,0.35,0.5,0.8,1.0时,支杆后端控制方案最大主动控制力分别为2 126 N,3 668 N,5 167 N,8 059 N,9 941 N,而振幅衰减85%所用时间分别为3.5 s,2.7 s,1.6 s,1.0 s,0.8 s。
4.2 前端控制方案FEM仿真
对于支杆前端控制方案,分别对控制参数λ=0.5,2.0,5.0,20.0等情形进行了FEM瞬态动力学仿真分析。模型前端点的y向振动位移和主动控制力的时间历程如图13和图14所示。从仿真计算结果可以看到,该前端控制方案能够使结构振动快速衰减。随着控制参数λ的增大,结构低频振动衰减加快,而控制力峰值亦快速增长。

图13 支杆前端控制方案位移时间历程

图14 支杆前端控制方案控制力时间历程
与第4.1节所给出的支杆后端控制方案计算相比,前端控制方案没有出现高频振动发散的情况。其原因是,前端控制方案控制点位于整个尾撑装置的前端,对于y向运动,此处受高阶振型的影响甚微,因此在此处施加控制力不会激发高频模态响应发散。
根据仿真计算结果,该前端控制主动抑振方案效果明显,控制参数λ=0.5,1.0,2.0,3.0,5.0时,最大主动控制力分别为850 N,1 668 N,3 214 N,4 648 N,7 277 N,而振幅衰减85%所用时间分别为3.5 s,2.1 s,1.0 s,0.6 s,0.4 s。
4.3 对比分析
以振幅衰减85%所用时间表示振动控制效果,支杆前端和后端控制方案的振动控制效果与控制力峰值对应关系如图15所示。由图可知,振动控制效果相同时,支杆前端控制方案所需的控制力显著低于支杆后端控制方案。因此,支杆前端控制方案是更为经济的方案。另外,根据4.1节和4.2节的分析,支杆前端控制的方案不会激发高频振动,而支杆后端控制方案在使用较大的速度反馈控制参数时会激发高频振动,导致振动恶化。综上所述,在工程许可的条件下,支杆前端控制方案为优选方案。

图15 方案效果对比
5 结 论
本文针对中国空气动力研究与发展中心4 m×3 m风洞尾撑装置进行了振动主动控制研究,提出了支杆前端或后端控制两种方案,基于有限元模态叠加法对两种方案进行了仿真分析。对比了两种方案的控制效果,为风洞尾撑装置振动控制方案选择提供了支持。
参 考 文 献
[1]恽起麟. 实验空气动力学[M]. 北京:国防工业出版社, 1994.
[2]梁 鉴,张卫国,王勋年,等. 4 m×3 m风洞无人机模型振动抑制系统研制[J].实验流体力学, 2004,21(4):65-70.
LIANG Jian, ZHANG Wei-guo, WANG Xun-nian, et al. Development for restraining oscillation device of the UAV model in the 4 m×3 m wind tunnel[J]. Experiments and Measure in Fluid Mechanics, 2004, 21(4):65-70.
[3]陈卫东,邵敏强,杨兴华,等. 跨声速风洞测力模型主动减振系统的试验研究[J].振动工程学报, 2007, 20(1),181-186.
CHEN Wei-dong, SHAO Min-qiang, YANG Xing-hua, et al. Experimental evaluation of an active vibration control system for wind tunnel aerodynamic models[J]. Journal of Vibration Engineering, 2007, 20(1),181-186.
[4]王 亮,陈怀海,贺旭东,等. 悬臂梁振动非接触式磁力主动控制研究[J]. 振动与冲击, 2010, 29(7):94-98.
WANG Liang, CHEN Huai-hai,HE Xu-dong,et al. Vibration active control for a cantilever beam with a noncontact magnetic force[J]. Journal of Vibration and Shock, 2010, 29(7), 94-98.
[5]Balakrishna S. Development of a wind tunnel active vibration reduction system[J]. AIAA 2007-961. 45th AIAA Aerospace Sciences Meeting and Exhibit, 8-11 January, 2007, Reno, Nevada.
[6]Fehren H, Hefer G. Validation testing with the active damping system in the european transonic windtunnel, AIAA-2001-0610. 39th AIAA Aerospace Sciences Meeting & Exhibit, 8-11 January 2001, Reno, Nevada.
[7]邹经湘,于开平. 结构动力学[M]. 哈尔滨:哈尔滨工业大学出版社, 2009.04.
[8]《数学手册》编写组. 数学手册. 北京:高等教育出版社, 2010.12.

