基于能量重心法的列车轴承多普勒畸变故障声信号校正诊断研究

张 翱， 胡 飞， 沈长青， 刘 方， 何清波， 孔凡让

(中国科学技术大学 精密机械与精密仪器系，合肥 230027)

列车轴承故障是列车故障的主要类型，也是影响列车安全的最大根源之一[1]。美国的一项统计表明，每年大约有50起跟轴承有关的列车出轨事故发生，而且这个数据已经持续保持了近10年的时间[2]。因此，加强轴承的监测和诊断，及时了解和掌握轴承的工作状态，可以尽量发挥轴承的工作潜力，避免或减少事故的发生，对列车的安全运行具有十分重要的意义。

轴承声音检测系统形成于20 世纪80 年代，系统组成如图1 所示，采用轨边监测麦克风阵列来采集轴承运行时发出的声音，通过分析轴承声音信号来判断轴承的运行状况。但由于麦克风放置位置与铁轨的不可忽略的约一米的距离以及轴承声源移动相对麦克风存在横向速度，产生了不同于雷达等领域多普勒效应的畸变声音信号，因此对其进行分析和校正是进行精确的轴承故障信号特征提取和诊断的前提。

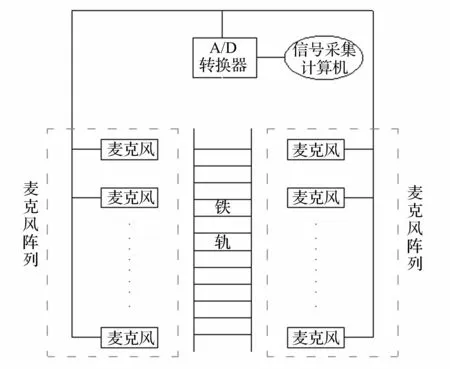
图1 高速列车轴承声音检测系统

20世纪90年代开始，Stojanovic等[3]提出了用锁相环技术(PLL)进行多普勒声音信号校正，随后Johnson等[4]在此基础上提出了锁相环技术与DFE算法相结合的校正方法，该方法适用于通信级别的信号校正；杨殿阁等[5]提出非线性时间映射法，基于声场中的运动学几何关系，建立声源与测量信号之间的非线性时间映射方法，采用运动声源的声源特征函数，在时域消除多普勒效应，但是该方法需要预测量列车行驶速度、初始位置和麦克风与铁轨横向距离等参数。近期Dybaa等[6-7]提出了局部扰动频率的概念，基于Hilbert变换求解瞬时频率对畸变信号进行重采样纠正，但该频域修正方法具有较多局限性，在特征频率分布比较密集的情况下难以进行有效的带通滤波，而且噪声的存在和滤波器的缺陷造成瞬时频率曲线的波动，从而带来校正误差。

本文提出了一种基于能量重心法的多普勒畸变校正方法，并将其应用在列车轴承道旁故障诊断中。首先由基于能量重心法的瞬时频率(IF)估计(IFE)来获取IF向量，在莫尔斯声学理论的基础上，对IF向量进行非线性拟合，进而得到重采样时间间隔序列，再对原信号进行重采样处理，即可实现多普勒畸变的消除。最后通过对仿真信号及列车轴承内外圈故障声信号的分析处理，验证了此种方法的有效性。

1 多普勒效应

当波源和观察者有相对运动时，观察者接受到的振动频率与波源振动频率不同的现象称为多普勒效应。

在列车速度为亚声速的情况下，考虑列车轴承声源为单极子点声源，并且传播介质为理想流体，即不存在粘滞性，没有能量损耗，其运动模型示意图如图2所示。根据莫尔斯声学理论[8]，从波动方程和运动关系出发推导可以推到得出以下公式：

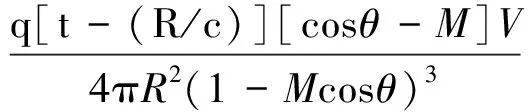
(1)

式中，P为麦克风处采集到的声压值，q为单极子点声源的强度，t为运行时刻，R为发声时刻声源与麦克风之间的距离，c为声音在介质中速度，θ为声源与麦克风连线与声源运动方向之间的夹角，V为声源速度，M=V/c为马赫数。式中第二项为小量，可以忽略不计。对于简谐声源q=q0sin(ω0t)有：

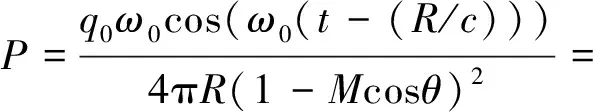
(2)

图2 运动模型示意图

在式(2)中，乘积符号左边的部分决定信号的幅值，右边的部分决定信号的相位。对相位进行求导即可得出频率随时间的变化。

(3)

式中，x为采集开始时刻时声源所在位置与麦克风位置水平距离，r为声源运动轨迹与麦克风的垂直距离，f0为运动声源信号频率，f为麦克风采集到的声音信号频率。由式(3)可以看出接收到的声音信号频率对比原信号频率呈现非线性畸变，因此本文所提出的方法即是针对此种信号多普勒畸变现象进行消除。

2 基于瞬时频率的多普勒畸变消除原理

信号的频率非平稳性的还原通常使用重采样方法，而建立一组重采样时间序列就是该方法的核心。对于多普勒畸变信号，瞬时频率与原信号频率(假设原信号为单一频率f0信号)存在如下关系[9]：

(4)

式中,n为周期内采样点数,fs为原信号采样频率,fsi为畸变信号i点处的采样频率，fi为畸变信号i点处的瞬时频率。

采样时间间隔即是采样频率倒数，即dt=1/fs，代入上式可得:

const=fi×dti=f0×dt

i=1,…,N-1

(5)

式中，dti即为重采样时间间隔，因此重采样时间间隔序列可以得出dtrsp=[dt1dt2… dtN-1]，从该时间间隔可以进一步计算出重采样时间点序列trsp=[0t1t2…tN-1]，重采样时间点序列以畸变信号的起始点为起始点，因此trsp(1)=0，计算公式如下:

(6)

由于重采样时间点超过畸变信号时间上限时，重采样将失去意义，因此定义重采样时间点序列上限为tM，即trsp=[0t1t2…tM]，其中M是不大于N-1的正整数，其值应满足:

(7)

多普勒畸变信号的瞬时频率f在任意区间[trsp(i)trsp(i+1)]内是连续变化的，所以采用某时刻的瞬时频率将会带来计算误差，设存在一个较大的整数值K，在时间dti/K内可以认为瞬时频率是恒定值，则:

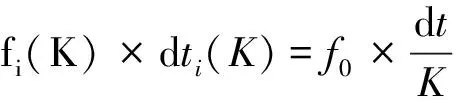
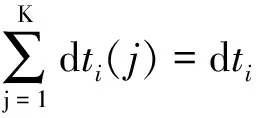
(8)

对区间[trsp(i)trsp(i+1)]内的K个时段求和可得:

i=1,…,M-1

(9)

当K值足够大时，上式可以用积分表示为:

i=1,…,M-1

(10)

由trsp(1)=0可进一步得到trsp(i) 的表达式为:

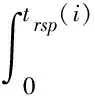
i=1,…,M-1

(11)

对上式进行求解即可得出重采样时间点序列trsp=[0t1t2…tM]，最后通过三次样条函数差值法对多普勒畸变信号x(t)进行重采样，从而得出校正后信号y(t)。

y=[y(dt)y(2×dt) …y(M×dt)]=[x(trsp(1))x(trsp(2)) …x(trsp(M))]

(12)

3 基于能量重心法的瞬时频率估计(IFE)

瞬时频率( IF )是非平稳信号分析中的一个重要概念，Ville于1948年提出的瞬时频率定义式是目前在学术界最为常用且得到了普遍认可。瞬时频率估计(Instantaneous Frequency Estimation-IFE)方法主要分为相位法、时频分布(Time-Frequency Distributions, TFD)法和希尔伯特黄变换(Hilbert-Huang Transform, HHT)[10]。相位法是利用信号的相位信息求取瞬时频率，主要有相位差分法和相位建模法。基于时频分布求取信号的瞬时频率的方法有用时频分布的一阶矩求取瞬时频率和峰值估计瞬时频率两种。HHT则是根据Hilbert变换求出实信号对应的解析信号，再利用解析信号求解瞬时频率。目前提供的瞬时频率估计方法大多只适用于单分量信号，对于多分量信号则先将其分解为单分量信号再进行计算。

对工程实际应用中的多分量信号，目前则主要是采用在STFT时频面上进行峰值搜索来估计瞬时频率。但是这种方法的估计精度依赖于频率分辨率邻近频率成分的干扰也会对估计精度产生影响，存在时频集聚性不是很理想的问题。另外，在求取多分量信号的IF时，一般通过时频滤波将其他分量遮掩，提取某一分量的IF，依次递推，增加了算法的计算量[11]。

离散频谱校正是用来解决离散频谱分析中时域截断和频域栅栏效应引起的误差、精确地提取频率成分的方法[12]。能量重心法则是根据对称窗函数离散频谱的能量重心特性推导出的一种离散频谱校正方法[13]，对于Hanning窗、矩形窗、Hamming窗、Blackman窗、Blackm an-Harris窗等对称窗函数而言，离散窗谱的能量重心都在原点或原点附近，利用这个特性可以进行频率的校正，幅值的校正则可利用巴什瓦定理进行。这种方法在分析平稳或准平稳信号时，具有较高的分析精度。但列车轴承声信号属于非平稳信号，不能直接使用离散频谱校正方法。因此，根据STFT算法原理，把短时间间隔的信号看成是准平稳信号，再通过叠代就能够利用离散频谱校正方法来校正整段信号的频谱。本文通过加Hanning窗的能量重心法在频域中对信号的频谱进行瞬时频率估计(IFE)，并通过离散频谱校正方法来提高分析精度。

3.1 能量重心法的原理

Hanning窗的功率谱函数为:

(13)

对任意一确定值f，G(f)满足下式:

n=∞

(14)

该式表明，Hanning窗离散频谱的能量重心无穷逼近坐标原点。由于Hanning窗旁瓣的功率谱值很小，根据其能量重心的特性，用主瓣内功率谱值较大的几条谱线可精确地求得主瓣的中心坐标。

对谐波信号其归一化加Hanning窗的频谱模函数的平方为:

(15)

相当于式(13)乘以系数A并平移到f=f0处，f0和A分别为分析谐波信号的归一化频率和幅值。

Hanning窗谱频率校正原理如图3所示，设Gi为功率谱第i条谱线值，Gk为主瓣内谱线最大值，k为幅值最大点对应的谱线号。

图3 Hanning窗谱频率校正

根据Hanning窗的能量重心特性有:

(16)

根据式(16)可以求得主瓣的中心:

(17)

设采样频率为fs，做谱点数为N，f0为主瓣中心，由式(17)就能得到能量校正法校正频率的通用公式[14]:

n=∞

(18)

3.2 基于能量重心法进行IFE的流程

基于能量重心法进行IFE的流程如下:

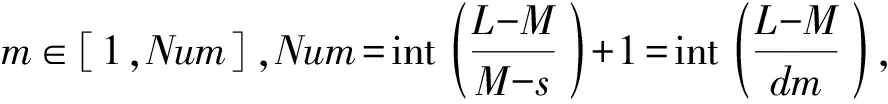
②选定初始搜索频率fsta频率搜索范围q,整周期采样系数k, 根据fsta和k计算出整周期采样点数N0；

③根据当前m，计算当前分段数据的起始点位置：p=(m-1)dm+1。在信号中截取M点数据{sig(i)},i∈[p,p+M-1]；

④以分析段中点为中心重新选取N0点作为新的分析段，并对其做加窗的DFT，求得搜索范围q内最大频率谱线位置以及其左右邻近的n条谱线的功率值。其中，n的取值与加窗的类型有关，这里加Hanning窗，n=2；

⑤利用能量重心法校正公式(18)对搜索到的峰值频率谱线进行频谱校正，得到校正频率f，令f为新的fsta，重新计算出整周期采样所需的采样点数N；

⑥如果N=N0或者达到最大迭代次数j时，f为分析段中点所对应的频率估计值，否则fsta=f，转步骤④；

⑦令m=m+1，返回步骤③，直到m=Num。

最终根据迭代求得的各段对应的IF，根据莫尔斯声学理论进行非线性插值拟合后得到IF拟合值。

4 基于IFE的多普勒畸变信号校正方法

4.1 多普勒畸变信号校正流程

多普勒畸变信号校正的流程图如图4所示，具体校正方法如下：

①对原始信号进行预处理。轴承声音信号中包含大量噪声，因此在分析前首先对其进行滤波处理。由于信号中趋势项的存在，会使时域中的相关分析或频域中的频率谱分析产生很大误差[15]，因此还应进行去除趋势项处理；

②采用STFT进行时频分析。通过时频谱，确定出步骤③所需求的初始搜索频率fsta，频率搜索范围q,整周期采样系数k；

③基于能量重心法的IFE。由3.2节所诉方法进行IFE，获得各段数据对应的IF；

④非线性拟合。根据莫尔斯声学理论进行非线性插值拟合后得到IF拟合值；

⑤多普勒畸变校正。由拟合后的IF计算出重采样的时间间隔序列，对原始信号进行重采样，以消除多普勒畸变；

⑥包络谱分析。通过包络谱解调出被调制的故障频率，判断出故障类型，由此验证本方法在列车轴承故障诊断中的有效性。

图4 多普勒畸变信号校正流程图

4.2 仿真信号模型的建立

根据公式(3)及莫尔斯声学理论，在此建立一个含有三个频率的信号进行仿真分析，其中设置这三个频率相近(f1=1 200 Hz,f2=1 300 Hz,f3=1 400 Hz)，由于经多普勒畸变后频宽有重叠，不能够简单地通过带通滤波器获得其中任何一个频率变化。采样频率设定为fs=50 kHz，这也是在后续实验中对列车轴承信号进行声音采集的采样频率。给定仿真参数x=5 m，r=2 m，c=340 m/s，以及v=20 m/s，仿真的原始信号时域图如下所示。

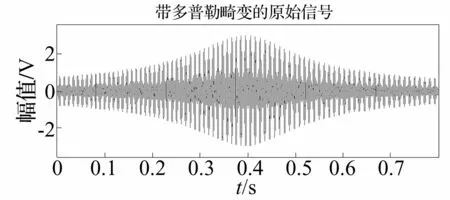
图5 带多普勒畸变的仿真原始信号

4.3 仿真信号校正结果

在本文中，由多普勒效应引起的时域幅值变化不是重点内容，因此在后续的信号处理中仅仅针对频域。由图6(a)可以看出仿真的多普勒畸变原始信号频率分布在1 000 Hz至1 600 Hz之间,其主要频宽Δf=342 Hz。由图6(b)原始信号的STFT图，我们可以清楚的看到三个设定频率的多普勒畸变现象。选取中间的频率进行IFE，在时刻t=0时，峰值大概出现在1 380 Hz处，因此搜索算法中设定1 380 Hz为起始点，设定频率搜索范围q为20 Hz，再通过基于能量重心法瞬时频率估计得到各段对应的IF。

图6 校正前后仿真信号的频谱对比

对得到的IF根据公式(12)进行非线性最小二乘法拟合，其IF拟合图如图7所示。拟合函数中有四个未知量，即是f0,r,v,x，通过拟合，我们即可获得这些参数。将拟合所得参数与设定的参数进行比较，如表1所示。

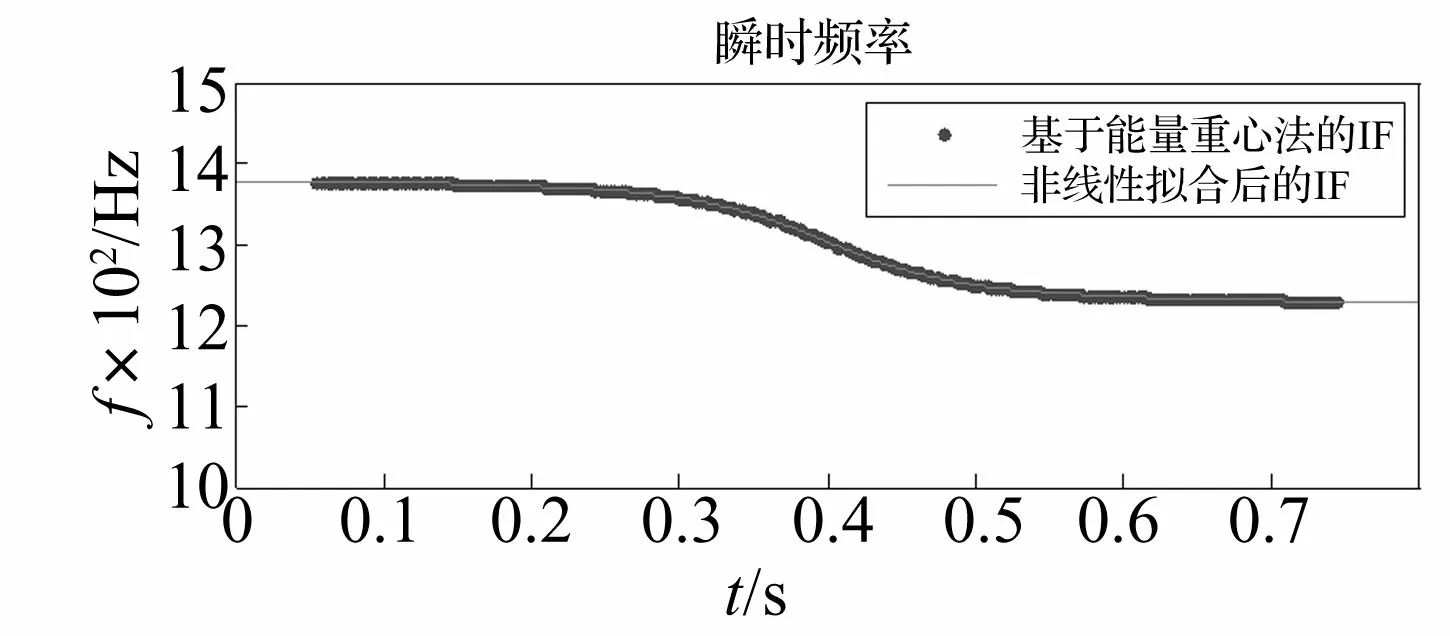
图7 中间频率的IF

表1 设定参数与拟合后所得参数对照表

最后，根据第二节描述的多普勒畸变信号校正方法，结合非线性最小二乘法拟合所得到的IF曲线，求解得出重采样时间点序列trsp，然后通过三次样条函数差值法对畸变信号的重采样，从而得出校正后信号。校正后信号的频谱及STFT图如图6(c)和图6(d)所示，可以明显的看出，三个频率均得到了很好的校正，而且从表1可以看出各参数的误差均符合要求，从而验证了该多普勒畸变校正方法的有效性。

5 道旁列车轴承声音信号故障诊断

我国列车使用的轴承是单列向心短圆柱滚子轴承，主要使用的型号是NJ(P)3226X1，因此基于该型号轴承本项目组自行设计了一套实验平台(图9(a))，用于获取静态列车轴承声音信号。实验中麦克风选用丹麦B&K公司的声压场麦克风4944-A，采集卡选用美国NI公司的PXI-4472动态信号采集模块，采集箱选用美国NI公司的PXI-1033机箱。轴承故障采用线切割方式人为加工而成，轴承内外圈的切缝均为0.18 mm,如图8所示。

图8 列车轴承内外圈故障

图9 多普勒畸变信号获取

实验中电机转速设置为1 430 r/min，轴承加载负荷为3 t,采样频率为50 kHz，由列车轴承实验平台采集到的信号为不含多普勒畸变的静态信号。如图9(b)所示，汽车以108 km/h的速度沿直线匀速行驶，其上固定一音响，以播放上面采集到的静态信号，麦克风安置于与汽车行驶轴向相距大约1.5 m处。

根据滚子轴承的运动关系可知，轴承外圈和内圈的故障频率可以由以下公式得出：

(19)

(20)

其中,fr是轴的旋转频率，实验中采用的是1 430 r/min,其他参数见实验所用的列车轴承规格参数表即表2。从式(19)，式(20)我们可以得出理论的外圈故障频率应为138.74 Hz，内圈故障频率应为194.93 Hz。

表2 列车轴承NJ(P)3226X1规格参数

对实验信号进行多普勒畸变校正的方法与上节所讨论的仿真信号校正基本是一致的，不同的是，实验信号比仿真信号包含更多的频率分量以及大量噪声，且是非平稳信号。因此在对其进行校正前，要首先进行去除趋势项及滤波预处理。图10为外圈故障信号，在图12(a)中我们可以清楚的看到,主要的频率分量集中在1 000 Hz到2 000 Hz之间，因此我们在这里只考虑3 000 Hz以下的频率分量。图11(a)为外圈故障信号的时频分布图，图中我们可以看到两个瞬时频率分量，由此就可以确定初始搜索频率fsta为1 350 Hz,选定搜索范围q为20 Hz，采用上节提到的方法进行多普勒校正。

图10 列车轴承外圈故障信号

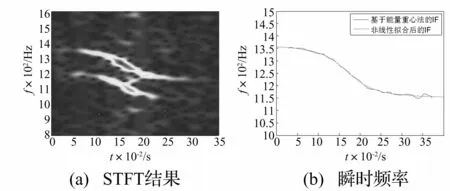
图11 瞬时频率估计

在图12(b)中可以看到校正前信号在故障频率处有个频宽为Δf的多普勒畸变，校正后的信号频谱及包络谱见图12(c) 和(d)，图中可以清楚的看到外圈故障频率f0为138.9 Hz,多普勒畸变已经基本消除，并且结果与理论值138.74 Hz十分接近。

图12 轴承外圈故障信号包络谱分析

下面对内圈故障信号进行分析，其时域图如图13所示。根据图15(a)，信号的主要频率分布在1 200 Hz到2 200 Hz之间，因此采用6 000 Hz的低通滤波器进行滤波。在图15(b)中，可以清楚的看到旋转频率fr，这是因为在低频的时候，多普勒效应不是十分明显，但是内圈故障频率在理论值194.93 Hz附近没有明显的峰值。由图14(a)可以大致确定初始搜索频率fsta为1 350 Hz,选定搜索范围q为20 Hz，通过校正之后，在图15(d)中我们就可以清楚的看到故障频率fi，但故障频率被旋转频率调制了，因此有边频带。此时fi为194.5 Hz，与理论值194.93 Hz也十分接近。

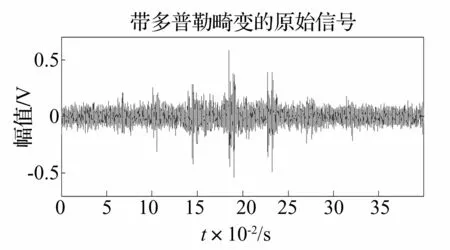
图13 列车轴承内圈故障信号

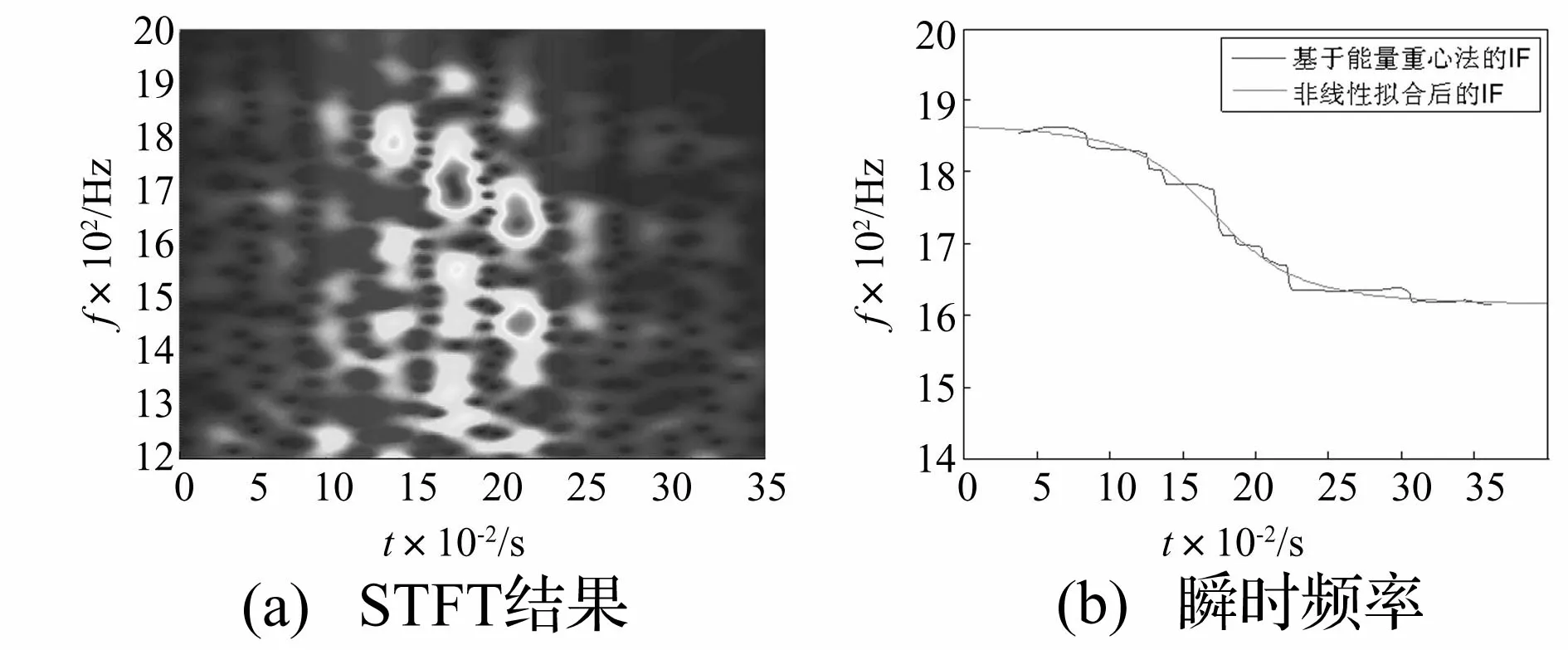
图14 瞬时频率估计

图15 轴承内圈故障信号包络谱分析

6 结 论

本文提出了一种针对高速列车轴承声音信号的多普勒畸变校正方法，并将其应用在列车轴承道旁故障诊断中。首先由基于能量重心法的瞬时频率(IF)估计(IFE)来获取IF向量，在莫尔斯声学理论的基础上，对IF向量进行非线性拟合，进而得到重采样时间间隔序列，再对原信号进行重采样处理，即可实现多普勒畸变的消除。通过对仿真信号进行分析处理后，由表1可以看出该方法的误差在容许的范围内。而通过对轴承信号进行多普勒畸变校正后能准确地判断出轴承的故障类型，证明了该方法在轨边列车轴承故障诊断中的应用是有效可行的。

与基于STFT峰值搜索及基于WVD峰值搜索的IFE相比，本文采用基于能量重心法的IFE有更高的精度，且分析精度受频率分辨率影响小，同时在信号的频域进行分析处理的方法，与以往在时域处理的方法相比，具有无需知道r、v和x这些参数的优点。但由于需要通过手动设置初始搜索频率、搜索范围和初始的整周期采样系数，也就无法实现离线无人诊断操作。为弥补此局限性，笔者将进行进一步的研究改进。

参 考 文 献

[1]Choe C H, Wan Y, Chan A K. Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals: comparison of FFT, CWT and DWT features[J]. SPIE Proceedings on Wavelet Applications, April, 1997, Vol. 3087, pp. 480-496.

[2]Irani F D, et al.先进道旁车辆状态监视系统的开发和应用[J].国外铁道车辆，2002, 39(2): 39-45.

Irani F D, et al. Development and deploymen t of advanced wayside condition monitoring systems[J].Foreign Rolling Stock, 2002, 39(2): 39-45.

[3]Stojanovic M, Catipovic J A, Proakis J G. Phase-coherent digital communications for underwater acoustic channels[J]. Oceanic Engineering, 1994, 19(1): 100-111.

[4]Johnson M, Freitag L, Stojanovic M. Improved Doppler tracking and correction for underwater acoustic communications[J]. IEEE International Conference on Acoustics, Speech, and Signal Processing, 1997, 1: 575-578

[5]杨殿阁，罗禹贡，李 兵，等. 基于时域多普勒修正的运动声全息识别方法[J]. 物理学报，2010, 59(07): 4738-4747.

YANG Dian-ge, LUO Yu-gong, LI Bing , et al.Acoustic holography method for measuring moving sound source with correction for Doppler effect in time-domain[J]. Acta Physica Sinica, 2010: 59(07): 4738-4747.

[8]Morse P, Ingard K. Theoretical Acoustics[M]. Science Press, Beijing, 1986.

[9]Cline J E, Bilodeau J R. Acoustic Wayside Identification of Freight Car Roller Bearing Detects[C]. Proceedings of the 1998 ASME/IEEE Joint Railroad Conference, 1998. 79-83.

[10]贾继德，孔凡让，王建平等.基于瞬时频率估计的内燃机信号阶比分析[J].内燃机工程, 2005, 26(3): 15-21.

JIA Ji-de, KONG Fan-rang, WANG Jian-ping. Order analysis of internal combustion engine signal based on instantaneous frequency estimation[J]. Chinese Internal Combustion Engine Engineering, 2005, 26(3): 15-21.

[11]郭 渝，秦树人.无转速计旋转机械升降速振动信号零相位阶比跟踪滤波[J].机械工程学报, 2004, 40(3): 51-54.

GUO Yu, QIN Shu-ren. Tacholess order tracking filtering for run-up or coast down vibration signal of rotating machinery based on zero-phase distortion digital filtering[J]. Chinese Journal of Mechanical Engineering, 2004, 40(3): 51-54.

[12]丁 康，张晓飞.频谱校正理论的发展[J].振动工程学报, 2000, 13(1): 14-22.

DING Kang, ZHANG Xiao-fei. Advances in spectrum correction theory[J].Journal of Vibration Engineering, 2000, 13(1): 14-22.

[13]丁 康，江利旗.离散频谱的能量重心校正法[J].振动工程学报, 2001, 14(3): 354-358.

DING Kang, JIANG Li-qi. Energy centrobaric correction method for discrete spectrum[J]. Journal of Vibration Engineering, 2001, 14(3): 354-358.

[14]段虎明，秦树人，李 宁.离散频谱的校正方法综述[J].振动与冲击, 2007, 26(11): 138-145.

DUAN Hu-ming, QIN Shu-ren, LI Ning.Review of correction methods for discrete spectrum[J]. Journal of Vibration and Shock, 2007, 26(11): 138-145.

[15]赵宝新，张保成，赵鹏飞,等.EMD在非平稳随机信号消除趋势项中的研究与应用[J].机械制造与自动化，2009, 38(5): 85-87.

ZHAO Bao-xin, ZHANG Bao-cheng, ZHAO Peng-fei, et al. Research on and application of EMD in eliminating trend Item of non-stationary random signals[J]. Machine Building and Automation, 2009, 38(5): 85-87.