基于H∞的铣削加工振动主动控制

郑平旭, 江 浩, 龙新华, 孟 光

(上海交通大学 机械与动力工程学院振动、冲击、噪声研究所，上海 200240)

振动是金属切削加工过程中广泛存在的现象。振动不仅会降低刀具使用寿命，工件加工质量，严重时甚至会引起颤振和整个加工系统的不稳定。再生颤振是引起振动的主要因素，在实际中最常见，对其研究也比较成熟。Tobias[1-2]在20世纪50年代对再生颤振的理论展开了研究并且都提出切削加工稳定性的解析解。Altitas[3]基于系统传递函数提出了预测系统稳定性图的频域方法。在切削振动控制方面，目前主要有主、被动两种控制方法。被动方法主要通过调节切削参数来避免系统不稳定，这样并不能真正提高加工效率[4]。主动方法通过改变被控对象在固有频率处的阻尼或者使用作动器直接抵消刀具或者工件的位移来提高系统的稳定性。随着作动器技术的发展，体积小，输出力大的的作动器被广泛应用，切削振动的主动控制有了更进一步的发展。Rashid等[5]设计了一个托盘装夹系统，利用压电作动器对动态切削力进行控制，从而实现了对切削加工中的振动控制。Rojas[6]利用磁致伸缩作动器和电流变高弹体阻尼器将主动和被动控制结合实现了对工件振动位移的控制。Claesson等[7]利用基于小波算法自适应控制器有效控制了振动，但是控制方法只是针对车削提出的。江浩等[8]利用鲁棒干扰抑制方法设计控制器驱动作动器实现了对铣削振动的抑制，但是该方法需要预先知道干扰频率特性，有一定局限性。铣削时由于刀具高速旋转且伴随进给运动使得振动位移信号采集十分困难，目前的主动控制要么针对刀具振动，要不就针对工件的振动。基于此，本文提出了针对刀具和工件相对振动的控制方法，并结合基于再生颤振建立的铣削模型，对其控制效果进行了数值仿真验证。

1 铣削模型建立

1.1 动态切削力模型

图1为圆柱螺旋立铣刀示意图,图中ba为刀具的轴向切削深度，η为刀具的螺旋角。把刀具的每一条切削刃看作是很多微元的组合，图1中右图表示左图中某条切削刃上微元Δz的切削受力图，对应的径向力、垂直于切削刃的力和摩擦力分别用ΔFr、ΔFτ和ΔFμ表示。

图1 圆柱螺旋立铣刀及其微元

通常情况下螺旋角不会为零，因此不能以正交切削的模型来定义切削力。然而根据Kronenberg[9]对非正交切削的研究，可以得到下列简化的切削力公式。

(1)

式中：Kt为切削系数(与材料有关)，φn为法向前角，μ为摩擦系数，c为切削力比例系数。h(t,i,z)为切屑厚度，可以表示为：

h(t,i,z)=Δxsinθi+Δycosθi+hsc

(2)

(3)

式中：f为进给率，θi为第i个齿转过的角度，Nt为刀齿数。Ω为刀具的径向切入角，可以表示为：

(4)

式中：d为径向切削厚度，R为刀具半径。

第i条切削刃微元Δz与其转角Δθi存在下列关系：

(5)

将微元力分解到刀具的径向(ΔFr)，切向(ΔFt)，和轴向方向(ΔFz)，得到：

(6)

由于我们只关心x与y方向的受力情况，将式(6)做如下分解，得到：

(7)

只要对式(7)进行在切削厚度方向上积分就可以得到整条切削刃在x和y方向所受到的力：

(8)

式中:θs和θe分别为第i条切削刃开始和结束切削的角度位置，对于逆铣和顺铣两种不同情况，可以分别表示为[10]：

逆铣

(9)

顺铣

(10)

式中:ω为主轴转速，Nt为刀具的齿数，φ为轴向切入角度，可以表示为：

(11)

将所有切削刃所受的力进行叠加就可以得到刀具在x和y方向上受到的力：

(12)

1.2 铣削系统的Simulink实现

图2 铣削系统动力学框图

2 主动控制器设计

考虑到铣削系统参数的不确定性，本文采用一种基于H∞的鲁棒混合灵敏度方法[12]来控制铣削加工过程中刀具和工件的相对振动。如图3所示，标准的H∞控制问题[12]就是求解控制器K(S)，使得闭环系统稳定，并使得传递函数的H∞范数最小。H∞控制不需对不同类型的不确定性进行区别对待以及在频域内加权处理，对非参数化不确定系统具有良好的控制效果，且控制器维数较小。由于切削振动主要由刀齿切入频率(TPF)的谐波成分组成。为了简化控制器维数，控制器设计时仅考虑TPF成分。被控对象为装有工件的主动减振平台，该主动控制平台的相关细节请参考文献[8]。

图3 标准H∞控制问题框图

这里以Y方向的振动控制为例，简要说明基于H∞的鲁棒混合灵敏度方法。该方法控制器设计流程如图4所示。

图4 控制器设计流程图

首先，测量被控对象Y方向的频响函数[11],使用Matlab系统辨识工具箱将其分别转化为名义参数模型。由于铣削过程是一个有时滞的动态过程，在建立主动平台Y向的名义模型时，需要使用Matlab控制系统工具箱中的pade函数来逼近真实的模型，其实质是一个时滞系统传递函数P(s)与拟合的传递函数Gy(s)(不含时滞特性)相乘来得到名义模型的传递函数G(s)。P(s)、Gy(s)和G(s)表达式如式(13)所示。图5中的虚线为主动减振平台Y向名义频响曲线，实线为实测频响曲线，通过对比，可以发现这两者很接近，可以利用名义模型来表示其传递函数。

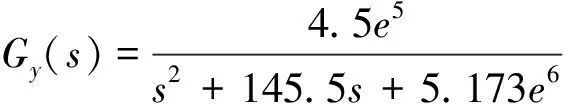
(13)

图5 主动平台Y向实测及名义模型频响函数

如图3所示， 基于H∞的鲁棒混合灵敏度方法的核心是选择合适的权重函数W1，W2，W3构造增强名义模型(augmented plant)。其中，G(s)为被控对象名义模型，u1为扰动输入，u2为控制输入，y1为评价输出，y2为量测输出。

受限于主动减振平台[8]中的作动器的输出力，文中所设计的控制方法只能有效控制TPF<200 Hz的铣削振动，因此将W1设计为低通滤波器的形式；W2为名义模型输入u的权重函数，将其设计为全波段衰减的形式；考虑到系统模型的不确定性，将W3设计为高通滤波器的形式。为降低控制器的阶数(名义模型阶数与权重函数阶数之和)，将W1，W2和W3采用式(14)所示表达式，其相应的伯德图见图6。

(14)

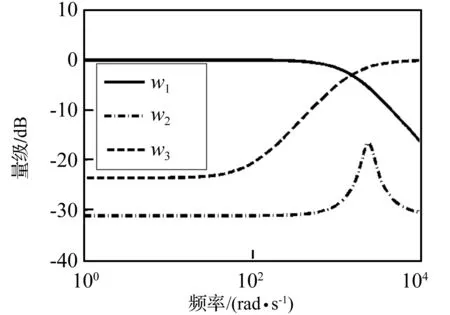
图6 加权函数伯德图

控制器K(s)通过Matlab鲁棒控制工具箱中hinfsyn函数计算获得。控制器K(s)表达式如式(15),伯德图如图7所示。

(15)

图7 反馈控制器K(s)伯德图

控制器及被控对象的闭环传递函数伯德图如图8。从图8可以看到，上述设计的闭环系统可以有效的实现低频阶段的鲁棒干扰抑制和高频段的鲁棒稳定性。

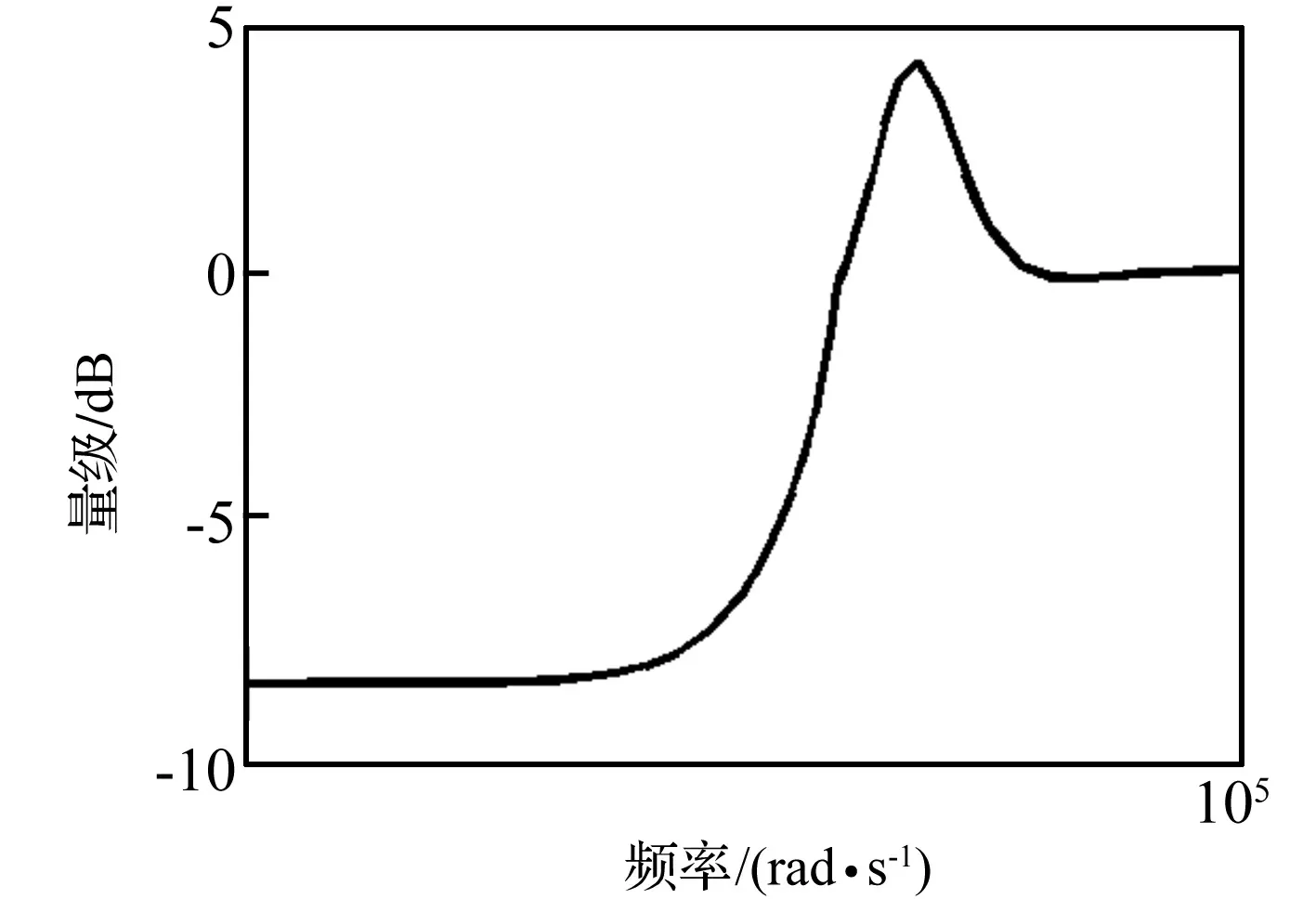
图8 闭环系统伯德图

3 主动控制仿真结果及分析

为验证控制器控制效果，结合第1节中的铣削系统动力学模型，采用Simulink进行了数值仿真。本仿真中铣削加工参数见表1中的第一组参数，其中刀具螺旋角30°，工件材料为淬硬钢。

图9 振动控制仿真实验1

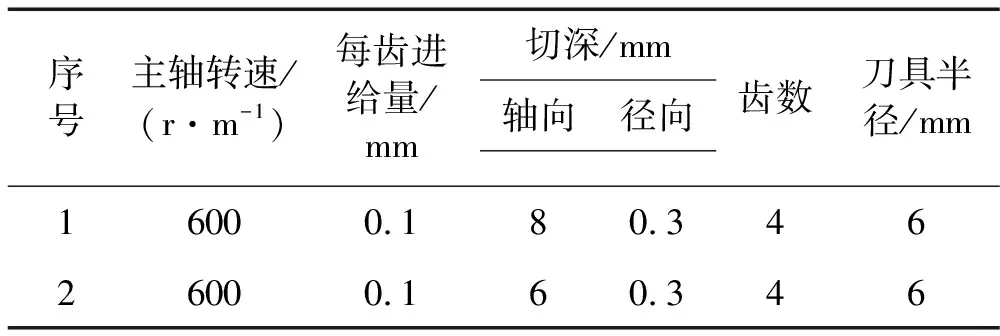
表1 铣削加工参数表

视刀具和工件的相对振动为扰动输入，仿真结果如图9所示。仿真结果表明，设计的控制器能够将轴向铣削深度较大的不稳定切削控制在稳定铣削区域，说明该控制器能够有效控制铣削振动。为了说明该控制方法对铣削颤振的抑制效果，对主轴在不同转速时的切削稳定性图进行了仿真计算，仿真参数为表1中第二组参数，只是轴向切削深度(ADOC)与主轴转速(Spindle Speed)为变量，结果如图10所示。对比图10中的两条曲线，可以发现没有施加控制的稳定性曲线整体低于施加控制后的稳定性曲线，说明基于H∞的主动控制方法可以有效控制铣削颤振的发生，扩大铣削的稳定性区域。

图10 主动控制稳定性图

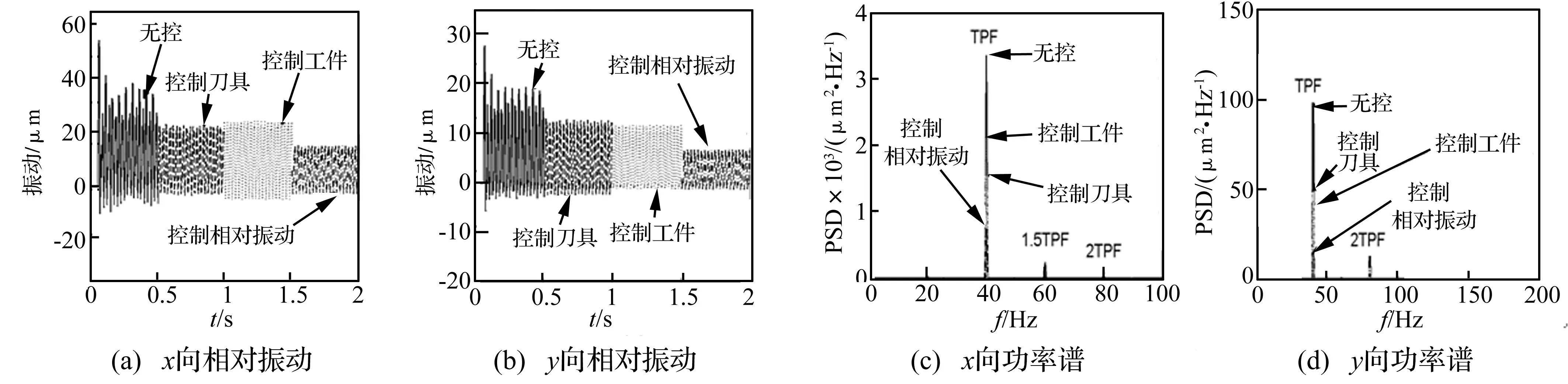
图11 不同控制对象控制效果比较

为了说明以刀具和工件的相对振动为控制对象的控制效果优于仅以刀具或者工件振动为控制对象的控制效果，以表1中的第二组参数进行铣削控制仿真，此时轴向切削深度为稳定切削深度，结果如图11 所示。

从图11可以看出，以刀具和工件的相对振动为控制对象的控制效果是优于仅以刀具或者工件振动为控制对象的。

4 实验论证

为了验证文中提出的控制方法的有效性以及第三节主动控制数值仿真的正确性，在DMU 70 V立式铣床上进行了多组铣削实验。铣削参数如表2 所示，实验中刀具螺旋角30°，工件材料为淬硬钢。

表2 铣削实验参数表

实验中使用NI PCI-6251数据采集卡，将采集到的刀具与工件的相对振动作为反馈信号，通过控制器，计算出控制信号，控制减振平台中的作动器产生主动力来抵消刀具与工件的相对振动。铣削主动控制结果如图12-13。

图12 振动控制铣削实验1

图13 振动控制铣削实验2

对比图11(c-d)(注：文中所有功率谱图中的箭头所指位置为其后文字所标情况下的峰值。)与图12(c-d)，可以发现实际铣削过程中相对振动的频谱成分要比仿真中复杂，比如主轴旋转频率(SF)成分。这是因为在实际铣削中，刀具在安装时偏心总会存在，这样便会引入SF成分；仿真模型中的传递函数是在系统静止时测量的，实际铣削时传递函数会有所不同；同时设计控制器时引入了权函数W1，W2，W3，实际系统并不存在，这些因素导致了频谱成分的不一致。

从图12(a-b)与图13(a-b)，可以发现文中提出的控制方法可以有效抑制铣削振动，提高铣削的质量。对比图12与图13 还可以发现，对于不同的铣削参数(见表2)的铣削实验，施加控制后振动幅值为未施加控制的40-60%，说明该控制方法具有一定的鲁棒性。

5 结 论

本文对铣削加工过程中的振动控制进行了讨论。视刀具和工件的相对振动为扰动，提出了基于H∞的主动控制方法，并进行了仿真与实验验证，证明了该控制方法能够有效抑制铣削颤振的发生，提高轴向铣削深度，扩大铣削的稳定性区域，并且具有一定的鲁棒性。仿真实验同时还说明视刀具和工件的相对振动为控制对象的控制效果优于仅以刀具或者工件振动为控制对象的控制效果。

参 考 文 献

[1]Tobias S A. Machine tool vibration[M]. New York:Blackie and Sons Ltd,1965.

[2]Koenigsberger F, Tluty J. Machine tool structures [M]. New York: Pergamon Press,1969.

[3]Altintas Y, Budak E. Analytical prediction of stability in milling [J]. Annals of CIRP-Manufacturing Technology, 1995,44(1): 357-362.

[4]薛 儒. 高速铣削中振动控制策略[J]. 世界制造技术与装备市场,2006,2(4):96-98.

XUE Ru. Strategies for calming chatter in high effective milling [J]. World Manufacturing Engineering & Market, 2006, 2(4):96-98.

[5]Rashid A, Nicolescu C M. Active vibration control in palletised workholding system for milling [J]. International Journal of Machine Tools & Manufacture, 2006, 46(8): 1626 1636.

[6]Rojas J, Liang C. Experimental investigation of active machine tool vibration control [J]. Proceedings of SPIE-International Society for Optical Engineering, 1996, 43(3): 373 384.

[7]Claesson I, Hakansson L. Adaptive active control of machine tool vibration in a lathe [J]. International Journal of Acoustic and Vibration, 1998 3(4): 155-162.

[8]江 浩，龙新华，孟 光. 铣削主动减振平台设计及控制[J].上海交通大学学报,2008,42(3):724-729.

JIANG Hao, LONG Xin-hua, MENG Guang. Design and control of active stage for vibration cancellation in milling [J].Journal of Shanghai Jiaotong University, 2008, 42(3):724-729.

[9]Kronenberg M. Grundzuge der Zerspanungslehre [M]. 2nd.Berlin: Springer, 1954.

[10]Liu X, Cheng K. Modeling the machining dynamics of peripheral milling [J]. International Journal of Machine Tools & Manufacture, 2005, 45(1):1301-1320.

[11]傅志方，华宏星. 模态分析理论与应用[M]. 上海：上海交通大学出版社，2000.

[12]梅生伟，申铁龙，刘志康. 现代鲁棒控制理论与应用[M].第二版. 北京：清华大学出版社，2008.