转速数对滑动轴承动力学系数影响研究
马文生, 陈照波, 焦映厚, Kirk R G
(1.中航工业沈阳发动机设计研究所,沈阳 110015;2.哈尔滨工业大学 机电工程学院,哈尔滨 150001;3.弗吉尼亚理工大学 转子动力学实验室,美国 24061)
在旋转机械中,转子-轴承系统存在油膜力、密封力等非线性激振力,导致系统存在不稳定的因素。轴承的参数变化对转子的动力学特性有明显的影响,由于轴承是阻尼的主要来源,进而控制着转子的响应;轴承的刚度和阻尼又影响着转子-轴承系统的临界转速和稳定性。所以在深入研究转子-轴承系统动力学问题时,必须考虑轴承对系统的作用[1-2]。谢友柏等[3]研究非线性油膜力和轴承外弹性阻尼对流体动压滑动轴承转子系统的振动特性的影响,建立了非线性运动方程式, 并开发了相关程序。袁小阳、朱均[4-5]基于周期解计算的打靶法和Floquet稳定性理论,给出了转子-轴承系统不平衡激励周期解及其稳定性非线性分析的数值方法,并用此方法研究了刚性转子-圆柱轴承系统中不平衡量对稳定性的影响。焦映厚和陈照波等[6-8]应用精度高、速度快的非线性油膜力数据库方法及非线性动力系统的稳定性和分叉理论对转子-轴承系统进行了分析,数值计算得到了转子- 轴承系统发生倍周期分叉时的分叉点及分叉图,揭示了不平衡转子-轴承系统从同步周期运动分叉发生一系列倍周期运动、最后导致混沌运动的过程。
本文以滑动轴承为研究对象,基于流体动力润滑控制方程推导出滑动轴承的Reynolds方程。利用DyRoBes软件[9-10]对决定轴承承载力的油膜压力进行计算及比较,分析并计算了不同的转速下的偏心率、最小油膜厚度、最大油膜压力、摩擦功耗、温升、临界轴颈质量、刚度系数、阻尼系数等影响滑动轴承油膜特性及动力学行为的重要参数。最后,在分析三维油膜压力时发现存在一个临界转速,当转速低于某个临界值时临界转速对最大油膜压力影响较大。
1 滑动轴承油膜力模型
滑动轴承由轴颈和轴瓦组成,轴颈一般比轴瓦的直径小0.1%~0.2%。轴颈和轴瓦之间存在一定的间隙,使得润滑油进入间隙形成油膜,由于流体的动压力产生了足够的承载力,并且循环的润滑油流过间隙起到降温作用,避免温度过高保证轴承正常工作[2,11]。

图1 轴颈的静平衡位置

图2 油膜厚度与油楔
图1是轴颈的静平衡位置图,其中o是轴瓦中心,o1是轴颈中心,W是静载荷,Ω是轴颈转速,e是偏心距,C是轴承的半径间隙,偏心率ε=e/C,ψ是偏位角,h是油膜厚度,ζ是从y轴顺时针方向的转角,静平衡位置由偏心距和偏位角决定。
油膜厚度和油楔如图2所示,图中最大油膜厚度和最小油膜厚度为:
hmax=C+e=C(1+ε)
hmin=C-e=C(1-ε)
(1)
任意位置的油膜厚度为:
h=C+ecos(ζ-ψ)=C[1+εcos(ζ-ψ)]
(2)
Reynolds方程是轴承油膜分析的基本方程:

(3)
其中:R是轴颈半径,p是油膜压力,η是润滑油粘度,z是轴瓦轴向坐标;
轴承分析的步骤一般为:通过Reynolds方程求解油膜的压力分布p(ζ,z),然后求轴承的静特性系数(最小油膜厚度、最大油膜压力、摩擦功耗、润滑油流量、温升、承载力、轴颈运动轨迹等)和动力特性系数。
对于无限短轴承L≪D,这样油膜力周向比轴向变化率小很多[12],即∂p/∂φ≪∂p/∂λ,这样Reynolds方程(3)的左端的周向函数可以忽略不计,因此Reynolds方程简化为:
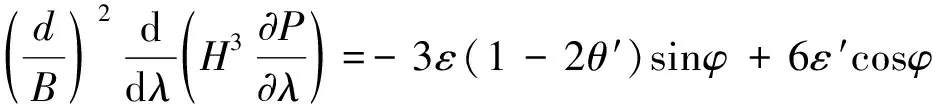
边界条件:

油膜力极坐标表达式:
(6)
极坐标无量纲表达式为:
(7)
则无量纲油膜力直角坐标表达式为:

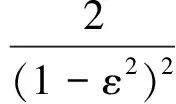
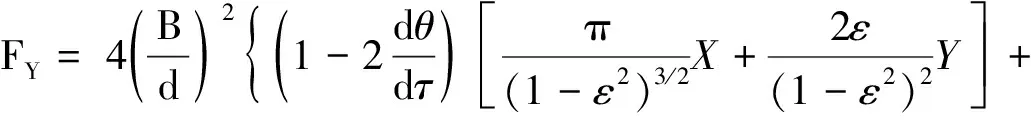
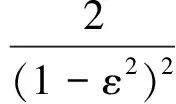
(8)
2 滑动轴承静、动特性系数影响因素研究
2.1 滑动轴承模型建立
轴承长度l=125 mm,轴承半径R=125 mm,轴颈间隙h=0.5 mm,润滑粘度系数μ=47×10-3Pa/s,计算转速3 000 r/min~12 000r/min,静载荷500 kg,通过DyRoBes-BePerf建模如图3所示:
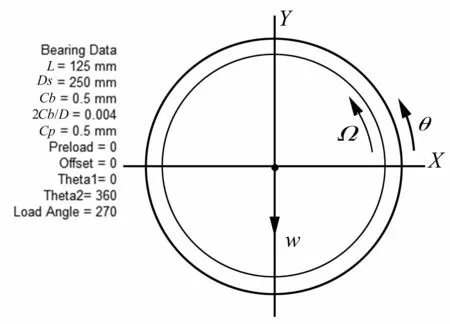
图3 轴承模型
2.2 转速对滑动轴承静、动力学特性影响研究
图4是转速对轴承动力学特性影响,其中包括转速对偏心率、最小油膜厚度、最大油膜压力、摩擦功耗、温升、临界轴颈质量、刚度系数和阻尼系数的影响研究。
图4(a)是当存在一个固定载荷W时,轴颈转速从1 000 r/min增大到12 000 r/min时转速对偏心率的影响研究,表明随着转速的增大偏心率减小,轴颈中心O′逐渐趋向于轴瓦中心O;图4(b)是转速对最小油膜厚度的影响,随着转速的增大最小油膜厚度增大,这是因为随着转速增大,轴颈中心朝着轴瓦中心运动,从而使得最小油膜厚度增大;图4(c)是转速对最大油膜压力的影响,图中可以看到转速从1 000 r/min增大到4 800 r/min时,最大油膜压力迅速减小,当转速大于4 800 r/min时最大油膜压力变化不大;图4(d)是转速对摩擦损耗的影响,从图中可以看到,随着转速的增大摩擦损耗逐渐增大,并且增大频率越来越大。

图4 转速对轴承动力学特性影响
图4(e)是转速对临界轴颈质量的影响,当转速从1 000 r/min增大到4 800 r/min时轴颈临界质量迅速减小,当转速大于4 800 r/min时轴颈临界质量变化不大;图4(f)是入口温度、工作温度和最大温度随转速的变化,图中可以看到随着转速的增大轴承工作温度增大;图4(g)是转速从1 000 r/min到12 000 r/min的主刚度和主阻尼的值,图中可以看到转速小于3 000 r/min时主刚度和主阻尼变大明显,当转速大于3 000 r/min时主刚度和主阻尼变化不大;图4(h)是转速从1 000 r/min到12 000 r/min的交叉刚度和交叉阻尼的值,图中虚线为负值,Kxy随着转速的增大而增大,Kyx随着转速的增大而负向增大,Cxy和Cyx相等并且随着转速的增大而减小。

图5 轴颈运动轨迹

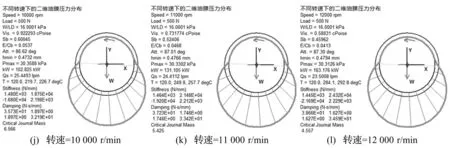
图6 不同转速下的二维油膜压力分布

图7 不同转速下的三维油膜压力分布
图5是轴颈运动轨迹图,图中可以看到随着转速从1 000 r/min增大到12 000 r/min时,轴颈中心向轴瓦中心移动。图6是不同转速下的二维油膜压力分布,从图6(a)~6(l)可以看到,随着转速的增大轴颈中心会随之变化,当转速为1 000 r/min时最小油膜厚度为0.183 2 mm,当转速增大到5 000 r/min时最小油膜厚度增大到0.428 3 mm,当转速增大到12 000 r/min时最小油膜厚度增大到0.479 4 mm;同时油膜压力分布和油膜压力幅值都有着显著的变化。
为了进一步得出油膜压力分布情况,本文进行计算了转速1 000 r/min到转速12 000 r/min共计12种三维油膜压力分析,并相应得出三维油膜压力的俯视图和切片图,如图7所示。图7(a)可以看到,当转速为1 000 r/min时偏心率为0.633 5,最大油膜压力为44.278 kPa;图47(e)为转速5 000 r/min时最大油膜压力分布图,此时偏心率为0.143 4,从图中可以看到最大油膜压力为30.714 5 kPa;图7(h)为转速8 000 r/min时最大油膜压力分布图,此时偏心率为0.073 9,从图中可以看到最大油膜压力为30.431 4 kPa;图7(l)为转速12 000时,此时偏心率为0.041 3,最大油膜压力为30.312 6 kPa。通过以上分析得到:随着转速的增大,最大油膜压力减小;存在一个临界转速5 000 r/min,当转速小于5 000 r/min时,增大转速时最大油膜压力会有较大变化;当转速大于5 000 r/min时,偏心率小于0.1,转速再增大只会引起偏心率微弱减小,最大油膜压力也会有微弱减小。最大油膜压力存在5 000 r/min临界转速原因:偏心率越大油膜压力越大,转速越大则偏心率越小,所以转速的增大会导致最大油膜压力的减小;对于本文模型,当转速为1 000 r/min时偏心率为0.633 5,而当转速增大到5 000 r/min时偏心率迅速减小到0.073 9,转速变化使得偏心率减小了0.559 6,而当转速从5 000 r/min增大到12 000 r/min偏心率只减小了0.032 6,偏心率是最大油膜压力的重要影响因素,偏心率的较大变化会引起油膜压力的较大、反之偏心率的较小变化也会使得最大油膜压力变化较小,分析结果与本文计算结果一致。
3 结 论
(1)本文建立了滑动轴承的动力学模型,并对其进行求解;
(2)研究转速对滑动轴承动力学特性进行研究,得到了转速对偏心率、最小油膜厚度、最大油膜压力、摩擦功耗、温升、临界轴颈质量、刚度系数、阻尼系数、二维和三维油膜压力的影响因素研究;
(3)在对三维油膜压力分析时发现存在一个临界值,当转速低于某个临界值时临界转速对最大油膜压力影响较大,当转速高于这个临界值时临界转速对最大油膜压力影响不大。
参 考 文 献
[1]黄文虎,夏松波,焦映厚.旋转机械非线性动力学设计基础理论与方法[M].北京:科学出版社,2006.
[2]钟一谔,何衍宗,王 正,等.转子动力学[M].北京:高等教育出版社, 1987.
[3]谢友柏,汤玉娣,夏松波. 具有非线性油膜力的滑动轴承转子系统振动特性研究[J]. 西安交通大学学报,1987,21(4):93-104.
XIE You-bai, TANG Yu-di, XIA Song-bo. Influence of non-linearity of hydrodynamic oil film forces on vibration characteristics of journal bearing-rotor system [J]. Journal of Xi’an Jiaotong University, 1987, 21(4):93-104.
[4]袁小阳,朱 均. 不平衡转子-滑动轴承系统稳定性的非线性研究[J]. 振动与冲击,1996,15(1):71-77.
YUAN Xiao-yang, ZHU Jun. Study on the non-linear stability of unbalance rotor bearing system [J]. Journal of vibration and shock, 1996, 15(1): 71-77.
[5]朱 均,虞 烈. 流体润滑理论[M]. 西安交通大学出版社,1986.
[6]焦映厚,李明章,陈照波. 不同油膜力模型下转子-圆柱轴承系统的动力学分析[J]. 哈尔滨工业大学学报,2007,39(1):46-50.
JIAO Ying-hou, LI Ming-zhang, CHEN Zhao-bo. Dynamic analysis of rotor-cylindrical bearing system with different oil film force models[J]. Journal of Harbin Institute of Technology, 2007,39(1):46-50.
[7]陈照波,焦映厚,陈 明,等.非线性转子-轴承系统动力学分叉及稳定性分析[J]. 哈尔滨工业大学学报,2002,34(5):587-590.
CHEN Zhao-bo, JIAO Ying-hou, CHEN Ming, et al. Dynamic bifurcation and stability analysis for nonlinear rotor bearing system[J]. Journal of Harbin Institute of Technology,2002, 34(5): 587-590.
[8]焦映厚,陈照波,夏松波,等.转子-非圆轴承系统非线性动力学行为的研究[J]. 航空动力学报,2000,15(6):413-418.
JIAO Ying-hou,CHEN Zhao-bo, XIA Song-bo, et al. Study on nonlinear dynamic behavior of rotor-non-circular bearing system[J]. Journal of Aerospace Power, 2000, 15(6): 413-418.
[9]Kirk R G, Alsaeed A, Gunter E J. Stability analysis of a high-speed automotive turbocharger[J]. Tribology Transactions, 2007,50,3:427-434.
[10]Kirk R G, Alsaeed A, Liptrap J, et al. Experimental test results for vibration of a high speed diesel engine turbocharger[J]. Tribology Transactions, 2008,51(4):422-427.
[11]张 文.转子动力学理论基础[M].北京:科学出版社,1990.
[12]张直明,张言羊,谢友柏.滑动轴承的流体动力润滑理论[M].北京:高等教育出版社,1987.

