好一道令人深思的奇函数试题——对一道高三教学调研试题的研究

●袁智斌

(深圳外国语学校 广东深圳 518083)

函数、奇函数等知识，既是高中数学教学的重点内容，又是学生学习中的难点．如何把握这些重点内容的教学并帮助学生突破这些难点？笔者认为既要开展“开口动脑记公式、悟其结构巧解题”[1]的数学知识和方法发生、发展的过程教学；又要在“以问题为中心”的解题分析过程中有效地渗透数学思想方法，进一步促进学生对数学知识和方法的深入学习和深刻理解．

本文通过笔者所任教学校高三数学调研卷上的一道奇函数填空试题的研究，指出该题的参考答案存在的错误，并结合此题的分析与解答来解析奇函数的定义，促进学生理解奇函数的本质．

1 答案对吗

原参考答案为：{0}或{-1,1}．

题目中“求函数定义域”的提法对吗？另外，此题给出的原参考答案对吗？首先，来看一下教材给出的函数定义：

一般地，设A,B是2个非空的数集，如果按某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，这样的对应叫做从A到B的一个函数，通常记为y=f(x),x∈A.其中，所有的输入值x组成的集合A叫做函数y=f(x)的定义域．给定函数时要指明函数的定义域．

从此定义出发，函数的先决条件之一就是必须先有“A,B这2个非空数集”以及某种确定的对应法则f，并且只有在它们满足了“如果按某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应”的条件下，“这样的对应叫做从A到B的一个函数”． 由此得出，函数的定义域是和函数“与生俱来”的，从而不能笼统地说对函数求定义域．也就是说在广义的情况下，泛泛地来谈“求函数的定义域”是一个伪命题．

华南师范大学的沈文淮教授多年前在讲课中提出过类似的观点[2]．笔者重提此点，主要是呼吁大家重新来审视平时教学中一些习以为常但又存在不足或不当之处的教学观点、提法和做法，以便进行改进，从而更好地发扬其优点．

其次，在默认“对于解析式表示的函数，如果没有指明定义域，那么就认为函数的定义域是使函数表达式有意义的输入值的集合”的情况下，此题的原参考答案完整吗？

2 分析与解答

我们首先明确奇函数的定义：

一般地，如果对于函数f(x)定义域内的任意一个x，都有f(-x)=-f(x),那么函数y=f(x)是奇函数．

1-x2≥0，

解得

-1≤x≤1，

因此，f(x)的定义域D必须满足D⊆[-1,1]，下面对D进行分类讨论：

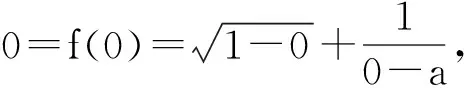
(其中常数a=1，定义域为D1⊆[-1,1))．

∀x∈D1,由0=f(-x)+f(x)得

解得

x=0∈[-1,1).

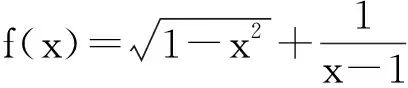
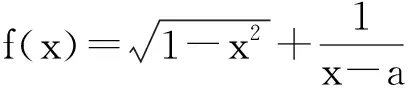
奇函数的定义蕴含着一个函数是奇函数的先决条件：函数的定义域D(φ⊂D)非空且关于原点对称，即：若∀x∈D，则-x∈D.因此，在任意取定x1∈D2⊆[-1,0)∪(0,1]后，该函数的定义域D2⊆[-1,0)∪(0,1]中将对应地存在一个-x1∈D2⊆[-1,0)∪(0,1].由题设条件知

0=f(-x1)+f(x1),

从而

(∀x1∈[-1,0)∪(0,1]且x1≠±a).

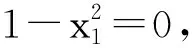
(其中a=0,定义域D2⊆[-1,0)∪(0,1]).

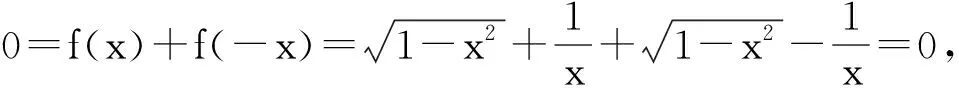
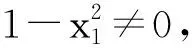
从而

(∀x1∈(-1,0)∪(0,1)且x1≠±a).

由此可知，原参考答案的解答过程与结论不完整，遗漏了满足题意的定义域

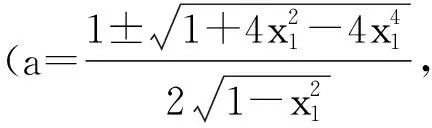
同时，原参考答案在表述上未准确反映出相应a的值，应在已求出的2个定义域“{0}或{-1,1}”的表述中及时补充相应参数a的值．

3 追问

在此，笔者提出以下问题进一步探寻：

答案也是否定的．原因在于：若假设D中存在2k+1(k∈N*)个元素，则由奇函数定义域的对称性，可知0∈D.当0∈D时的情形前面已讨论，得到D1={0}(其中a=1)，这与假设矛盾．因此，当D为有限集时，D中元素的个数不能为大于1的奇数．

问题3和问题4留给有兴趣的读者研究．

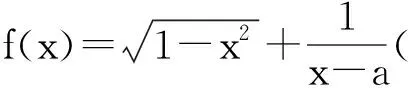
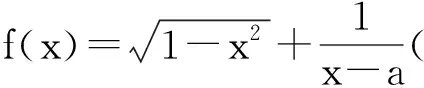
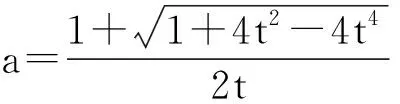
若a≤-1，则g(0)>0，g(1)>0，且g′(t)=3t2+a2-1≥0 (t∈[0，1])，从而g(t)在[0，1]上无零点，即所求定义域为空集,这与函数的定义域非空矛盾．

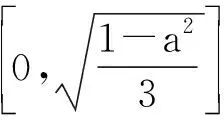
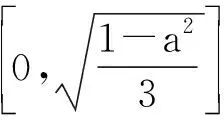
4 建议

其一，该题原参考答案的解答不完整从一个侧面折射出奇函数等重点、难点知识在教与学的方式、方法上有待于改进与深化．数学教学中应该注重探寻数学知识、方法的教学与数学解题能力培养之间的内在联系与关系，并通过科学地开展数学知识方法的深入教学来更加科学、高效地促进学生解题能力的提高．

其二，建议在今后新修订的《普通高中数学课程标准(实验稿)》、新版教材和试卷等，可将“求函数的定义域”修改为：求使函数解析式有意义的自变量的取值范围．

其三，建议教师在平时教学中要注意自觉遵循波利亚在《怎样解题》中提出的“回到定义上去”的谆谆教导，从而更加科学、有效、自如地开展教学、启迪学生．

其四，该题不宜编排在高三教学调研卷的填空题处，更不宜编排在文科数学调研卷上的填空题处．若安排在高三文、理科数学卷的解答题部分，则将会更加彰显此题的价值和功能．

[1] 陈都，王玉清，舒敬华，等.数学娱乐圈[J]．数学通讯，2004(17)：49．

[2] 袁智斌．系统扎实的研究生教育令我们受益终生[J].中学数学研究，2007(4)：15-17.

[3] 谢邦杰．抽象代数学[M]．上海：上海科学技术出版社，1982．

[4] 华东师范大学数学系．数学分析(下册)[M]．北京：高等教育出版社，1981．