构建高中数学本真课堂的实践探索

●郑日锋

(学军中学 浙江杭州 310012)

自国家新课程标准实施后，教师的教学观发生了较大的改变，课堂教学行为也发生了一些改变，在全国、省、市的一些优质课评比或展示中可见一斑.但是“穿新鞋、走老路”的现象依然存在，许多教师在高考的指挥棒下，为了片面追求升学率，在数学课堂上满堂灌，进行大容量教学，无视学生的认知规律，无视数学学科本质，无视教学的育人功能，停留在知识教学层面，导致许多学生丧失了学习兴趣.许多教师把数学课堂简单地看作“传递数学知识的地方”，教师讲，学生听，教师示范，学生模仿，学生一直以来在“模仿、练习、记忆、熟练”不断循环中学习数学，导致许多学生认为数学是枯燥乏味的，讨厌数学，惧怕数学.为了学生的终身发展，我们的教学既要指向当前，又要指向学生的未来，不能以透支学生的未来兴趣为代价，改变这种“快餐式”的数学课堂教学，是时代的要求.构建本真的数学课堂，让数学课堂成为具有师生生命意义的课堂，是当下每一位数学教师需要探索的课题.

1 对本真数学课堂的认识

所谓本真的数学课堂，就是遵循教与学的规律，实现学生、教师、文本、教学资源的交互作用，体现教师的主导与学生的主体，让教学效果最大化.而构建本真数学课堂需要以下3个理论的支持.

1.1 基于学生发展的需要

数学对于人类理性精神的养成与发展有着特别重要的意义.数学学习使人类学到了一些处理问题的基本思想方法，有能力掌握相应的数学工具解决将来在专业工作中遇到的困难.

1.2 基于3个理解

理解数学.重数学本质的揭示与思维过程的暴露，重知识的发展过程与知识间的逻辑关系，重数学概念的理解与深化，重数学思想方法的提炼与总结.

理解教材.教师对教材的理解体现教者本色，对教材内容按教的视角进行重构，尊重教材而不盲从教材，从“教教材”到“用教材教”再到“创造性使用教材”.

理解教学.教学的艺术不在于传授的本领，而在于激励、唤醒和鼓舞.教师做学生学习的引导者，在学生已有的认识基础上因势利导，通过启发、点拨，引领学生自然走到教师预设的方法中来，实现教与学的和谐统一.

1.3 基于意义学习

奥苏贝尔在其提出的意义学习理论中指出，意义学习所必需的2个内部条件是：(1)学习者具有同化新材料的认知结构；(2)学习者具有学习新材料的学习心向.前者涉及教学的认知维度，即教材内容为学生可接受；后者则涉及教学的情感维度：教材内容为学生乐接受.前者是教材编写者的主要任务，后者则是教师工作的艺术性体现——即怎么从学习形式上使得教材内容与学生更匹配.

2 构建本真数学课堂的教学实践

本真的高中数学课堂，在追求教学特色的同时有哪些核心要素呢？笔者以案例的形式试图探寻核心要素及其教学作用.

2.1 导

以境育情，促进学生迅速进入角色，引起学生的学习兴趣或获得情感上的共鸣，为顺利展开教学作好铺垫.

情境创设要着眼于：贴近学生的生活实际；有一定的思考价值；学生能感悟又蕴藏教材知识；体现时代精神；帮助学生建立数学概念、公理、公式、定理等数学模型，引发学生认知上的冲突，激发探究的热情.

一堂成功的数学课，是从精彩的导入开始的，正如郑毓信教授所指出的，情境设置不应该仅仅起到“敲门砖”的作用，还应当在课堂的进一步开展中自始自终发挥重要的向导作用.

案例1 指数函数的导入

现在将一张报纸反复进行对折，请学生们完成表1：

表1 对折x次后报纸的厚度和面积

学生完成表格后，教师给出以下问题：

(1)试写出报纸厚度y与折纸次数x之间的函数关系式；

(2)试写出报纸面积y与折纸次数x之间的函数关系式.

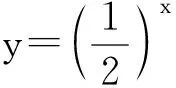
本教学片段从学生熟悉的折纸试验出发，得到2个特殊的指数函数模型，这2个特殊的指数函数不是以前学过的函数类型，需要新命名，从而自然引出指数函数的定义.而且这2个特殊的函数分别代表“底数大于1的指数函数”与“底数大于0而小于1的指数函数”，为研究指数函数的性质埋下伏笔.

2.2 味

让数学味充溢课堂，设置问题链，锤炼学生的数学思维，提高数学素质，需要教师上的每一节课都有1个中心——数学核心，以及2个基本点——教师的点拨与学生的领悟.

案例2 椭圆第1课时的教学片段

师：(完成了椭圆的定义教学后)刚才我们得到了椭圆的定义，怎样才能更深刻地认识椭圆呢？

生1：建立椭圆的方程，利用椭圆方程研究椭圆的几何性质.

师：很好！我们现在探究椭圆的标准方程.有哪些步骤？

生2：建—设—限—代—化—证.

在学生建立了如图1所示的平面直角坐标系后，教师提出问题：前面我们通过几何画板，把圆变成椭圆，现在能否借助圆的方程类比猜想出椭圆的方程？

(先独立思考，再小组交流.)

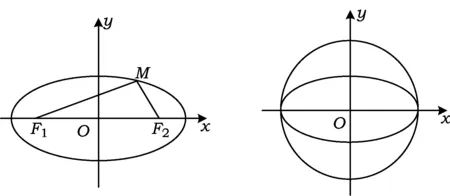
图1 图2

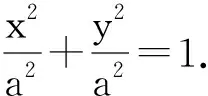
师：学生3利用类比推理及椭圆与圆的关系猜想椭圆的方程，猜想得到的结论是否正确？如果正确，需要给出严格的证明.

生：猜想正确，利用求曲线方程的方法给出证明.

(下略.)

本教学片段跳出常规教学的视角，从再创造教学的视角，启发引导学生从以原点为圆心的圆方程，大胆猜想椭圆的标准方程，然后让学生证明猜想，凸显了数学的本质，让数学课散发出浓郁的“数学味”；通过展现数学发现的过程，激发学生的创新意识；培养了学生的合情推理能力，把复杂的数学知识变得简单明了.

2.3 奇

在中学数学教材中，有些章节的内容显得比较浅显，学生一看就懂，需要教师化平淡为奇妙，挖掘其中蕴含的丰富思想及数学意蕴；还有些章节概念深奥，大部分学生难以理解，需要教师化奇妙为平淡，搭建脚手架，基于符合学生认知水平进行教学设计.

案例3 古典概型的教学片段

出示问题：抛掷2枚质地均匀的硬币，出现一正一反的概率是多少？

师：此问题的答案是多少？

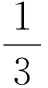
接着教师给出了2个试验：

试验1 抛掷一枚质地均匀的硬币.

试验2 抛掷一颗均匀的骰子.

首先引导学生建立古典概型这一重要的概率模型，并探索出古典概型中随机事件的概率公式，再让学生探讨课前问题.

本教学案例中，古典概型对学生来说并不陌生，在初中教材中就接触过，属于学生一看就懂的内容.教师从一个具体问题的2个不同答案出发，引发认知冲突，激发学生的求知欲.因为要解决问题，所以需要建立数学模型，然后以2个试验为载体，通过师生互动对话，不断促进学生思考，让学生经历观察、归纳、猜想、验证的数学探究过程,体现“化平淡为奇妙”.

2.4 活

新课程倡导在教师主导下的学生自主学习的过程，这就要求在课堂教学设计中，教师要进行换位思考，想学生之所想，走进学生的数学学习心理，实现教师的所想与学生的所思“浑然一体”，师生的思维得到升华.

案例4 参数方程概念的教学片段

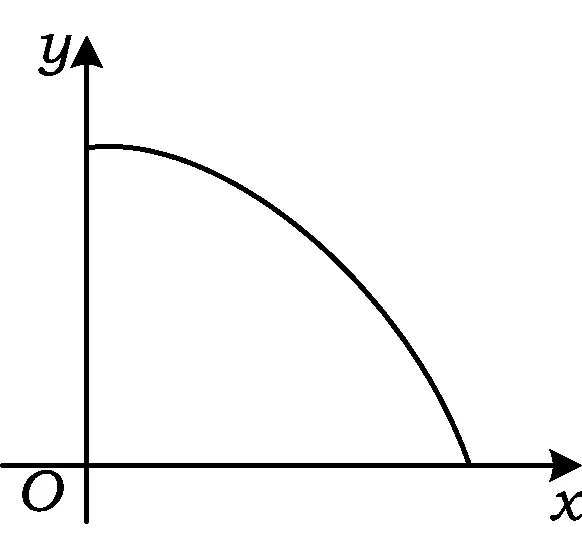
图3

首先给出问题：假设“愤怒”的小鸟以初速度5 m/s水平抛出，小鸟距地面高度为1 m，取g=10 m/s2，你能提出什么问题？

生：(1)求小鸟到达地面的时间；(2)求小鸟运动的轨迹方程.

师：请同学们尝试求小鸟运动的轨迹方程.

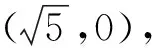
师：为什么是二次函数的图像，还有其他方法吗？

生2：小鸟的运动可以分解为：水平方向作匀速直线运动，竖直方向作自由落体运动.设在时刻t小鸟到达点M(x,y)，则

师：很好！你能否证明小鸟运动的轨迹是抛物线？

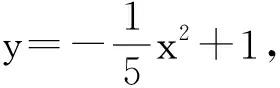
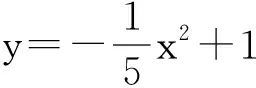
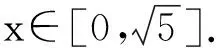
生2：t起了过渡作用.

师：我们把此方程组取个名字，叫做曲线的参数方程.今天我们就参数方程的意义作一些探讨.

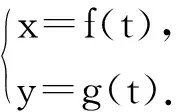
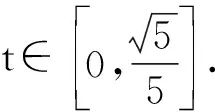
在本教学片段中，教师以愤怒的小鸟的运动轨迹引入课题，源于对运动的研究，学生对平抛运动是熟悉的，让学生感悟到参数方程是抛物线的另一种形式，参数是媒介.教学过程中充分重视了知识的发生、发展过程，没有把知识硬塞给学生，而是自然地、水到渠成地让学生接受知识，并且让学生经历不断地完善知识的过程，获得情感上的共鸣，让教师所想与学生所思“浑然一体”.

2.5 实

教师把自己置于困境中，并再现自己或数学家从中走出来的过程，让学生看到教师或数学家的真实思维过程是怎样的，让数学思想随着“数学知识”的“春风”潜入学生的脑海中.

案例5 二项式定理的教学片段

1664年冬，牛顿在研读了沃利斯博士的《无穷算术》后思考：

(a+b)2=(a+b)(a+b)=a2+2ab+b2,

(a+b)3= (a+b)(a+b)(a+b)=

a3+3a2b+3ab2+b3,

(a+b)4= (a+b)(a+b)(a+b)(a+b)=

a4+4a3b+6a2b2+4ab3+b4，

对任意正整数n,(a+b)n有怎样的结果呢？

请观察(a+b)2,(a+b)3,(a+b)4的展开式，并思考：展开式中的项是如何得到的？展开式中各项的系数是如何确定的？你能猜想(a+b)n的展开式吗？

本教学片段以牛顿的思考引发学生探究，让学生感悟数学家思考问题的方法与角度，能激发学习的兴趣及创造性.

2.6 疑

让学生带着作业的同时，能带着问题依依不舍地走出课堂.

案例6 随机变量的均值与方差习题课

问题1 一个口袋里装有大小相同的3个红球和2个黄球，从中任取2个，求其中含红球个数X的均值与方差.

问题2 一个口袋里装有大小相同的3个红球和2个黄球，从中有放回地取球2次，求其中含红球个数X的均值与方差.

课堂上解决了问题1和问题2后，教师提问：

(1)问题1中的X服从什么分布？(答案：超几何分布.)

(2)问题2中的X服从什么分布？(答案：二项分布.)

(3)这里的超几何分布与二项分布的均值相等，而方差不等，这是偶然的巧合吗？

本教学片段通过布置课外探究式作业，将课堂知识向课外延伸，让师生在自主、合作、探究中锻炼思维，体验求知的艰辛与快乐，实现教学的双赢.

结束语 构建本真的高中数学课堂，旨在使数学课堂焕发活力，使课堂成为教师与学生共同成长的舞台，打破数学课堂“千人一面”的现象，从学校层面，打造具有学校特色的课堂教学，从教师个体层面，打造具有个人特色的课堂.