例谈“学为中心”理念下自主课堂的教学设计

●方云兵 陈美英

(浙江师范大学婺州外国语学校 浙江金华 321025)

现代教学论认为，教学过程归根到底是如何教会学生学习.“学为中心”的数学课堂就是把学生学习作为教学中心，以学生自主学习、自主思考解决问题为主要学习形式，通过教师启发学生思考达到深入理解数学的一种教学形式.“学生怎样学，怎样引导学生学，怎样帮助学生学”是“学为中心”的精髓.本文试着从“三理解”的角度,即：理解教材、理解学生、理解数学的角度，通过3个教学设计的案例谈谈自己的一些做法.

1 理解教材——关注“怎样引导学生学”

在对教材进行分析时，坚持宏观把握教材、微观分析教材，树立“整体教材观”，既要分析教学内容所在节的教材处理、理解章前图的内涵，又要看到这部分内容在整章中的地位和作用，甚至各种版本教材对这节内容的处理，这样就能从整体上理解本节内容，更深入理解教材对于这部分内容及其相关内容的编写意图.首先要理解教学内容，弄清“是什么”，明确例题的地位和作用，弄清习题与例题的关系，揣摩插图的编排意图，钻研提示语和旁注；其次要理解教材整体结构及前后关系，在概念体系中认识核心概念；最后要理解教学内容所反映的思想方法.在依托教材的基础上，根据实际需要把教材内容通过问题的形式，对学生的有效思考进行启发，最大程度地发挥教材的功能，把着力点放在“怎样引导学生学”上.

案例1 “尝试检验法”的教学设计(浙教版七年级上册第5.1节“一元一次方程”)：

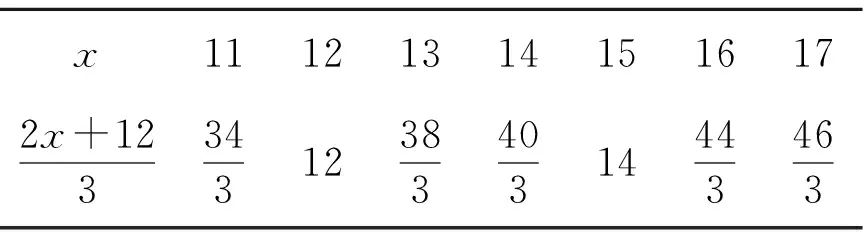
表1 代数式对应值

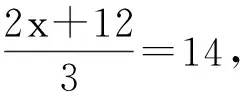
教材的设计本意是衔接合作学习问题(3)(小强、小杰、张明参加投篮比赛，每人投了20次．小强投进10个球，小杰比张明多投进2个，3个人平均每人投进14个球．问小杰和张明各投进多少个).但是在实际教学过程中，绝大多数学生都是采用小学所学的逆运算的方法解方程(班级44位学生，只有10位学生采用尝试检验).学生们很困惑，明明可以用小学的逆运算解简单方程的方法直接求解，为什么要这么复杂进行尝试检验呢？这样的教学设计重教材、轻学生；重接受、轻理解；重结果、轻过程.在教学时教师讲到为止，学生听到为止，速战速决，思想过程匆匆而来又匆匆而去，学生就囫囵吞枣地接受了，而没有进行思想方法的引导.学生对方程解的探究过程带有一定的盲目性，完成不了知识内容的内化和数学经验的积累，更没有从质和量上丰富原有的思想方法.

设计改进 在上一环节让学生自学判断t=3是不是方程3t+1=7的解后思考：刚才我们在计算时发现，t=3不是原方程的解，那么方程的解是比3大还是比3小？你是怎么想的？

生：当t=3时，左边=10，比右边大，说明取值太大了，应取比3小的数.

师：你会试着取几？

生：取t=2.

师：按照刚才总结的判断一个未知数的值是否为一元一次方程的解的方法和程序(代、算、比、判)，试一试.

这种求一元一次方程解的方法叫做尝试检验法！

设计意图 通过这一环节完成从“一元一次方程的解”教学环节过渡到“尝试检验法解方程”，让学生的思维有一个顺势而上的过程.

然后指导学生阅读教材内容，思考以下问题：

师：x必须是整数吗？

生：因为进球数不可能是小数，所以肯定都是整数.

师：通过分析，方程解的范围缩小了！

师：x可以取21，20吗？

生：21不行，因为题目要求每人投20次.20也不行，如果是20的话，小杰就投了22次了，不符合题意.

师：通过分析，未知数的范围又缩小了！

此时，教师又追问：x可以取9，10吗？

生：不可以，因为平均数是14，小强只投进了10个球，另外2个人要比他投得多，平均数才会到14.

教师和学生一起归纳：尝试检验法的一般步骤(略).

设计意图 通过4个问题迫使学生不断思考未知数取值的方法，体验尝试未知数取值的缩小过程.

跟踪练习 对于方程3x-8=x，表2已给出部分未知数的值,请回答下列问题．

表2 方程对应值

(1)表2中a=______,b=______，思考：方程的解应在哪2个整数之间？

(2)写出方程3x-8=x的解.

设计意图 尝试检验法是这节课的难点，笔者在处理时，增添教学环节间的过渡，深挖学生阅读文本时容易“滑过”之处，设计启发学生深度思考的问题，通过不断追问，顺着人们的认知规律把判断一个未知数的值和尝试检验法这2个知识点自然地衔接在一起.重新编制尝试检验法的教学素材，由于教材例题中的数都是整数，给学生造成不科学的尝试路径，这又是本节课的一个难点，于是教师改编了上面的跟踪练习，其目的是：使学生体会逐渐逼近的思想，把单纯地填表格(代数式求值)变为开放地思考；使学生明白尝试取值时，既可以是正数，也可以是负数，还可以是小数.这样既加强了对未知数取值的学法指导，又引导学生对学习信息进行整理归纳,使学生完整经历尝试检验、尝试取值的过程.

2 理解学生——关注“学生怎样学”

在课堂教学中要始终坚持以学为中心，从学生的认知水平出发，以学定“问”，充分考虑学生已有的经验、学习基础、思维特点，立足于学生的“最近发展区”，用学生的眼睛看数学，由感性到理性、由浅入深地设计问题，真正引导和帮助学生思考问题、分析问题和解决问题.

案例2 九年级上册第1.1节“反比例函数概念”巩固问题设计(案例来源：浙江省金华市开发区优质课评比).

1.下列函数中,y是x的反比例函数吗？如果是，比例系数k是多少？

2.辨析题:兄弟2个人分吃1碗饺子，每人吃饺子的个数如表3所示:

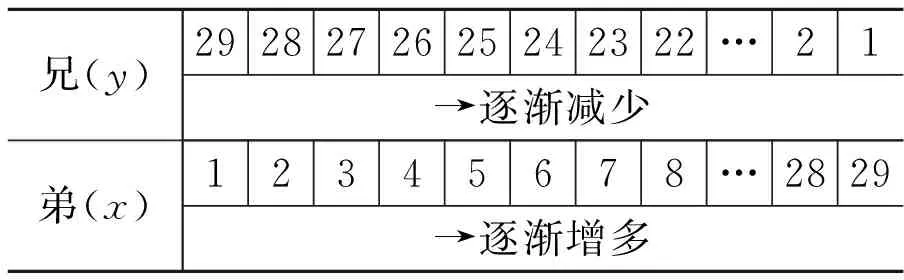
表3 每人吃饺子的个数

(1)写出兄吃的饺子个数y与弟吃的饺子个数x之间的函数关系式(不要求写x，y的取值范围)；

(2)因为当弟吃的饺子个数x增多时，兄吃的饺子个数y在减少，所以y与x成反比例,你认为对吗？说说你是怎么想的.

3.y是x的反比例函数，表4给出了x与y的一些值:

表4 x与y的对应值

(1)写出这个反比例函数的表达式;

(2)根据表达式完成表4.

教师通过设计2个练习暗含反比例函数的2种表示方式(解析式法、表格法)，使学生在辨析中深刻理解反比例函数的本质.在巩固练习2中，把学生存在的疑点、易混点呈现给学生.从字面上理解“反比例”，学生就有“增大而减小”这一首印象，再加上学生受小学所学和七年级科学相关知识中的成反比例关系的负迁移的影响，认为只要一个量增加、一个量减少就是反比例函数，特别是表3中的“逐渐增大”与“逐渐减少”更有迷惑性.这样设计的优点是通过学生的活跃争执以理服人，最后回到反比例函数的概念上，达到“理越辩越明”的教学效果.这个过程真正做到了“学为中心”，既关注结果，更关注过程.列表法本身也是函数的3种形式之一.设计表格的形式，把反比例函数的解析式隐藏在表格中，先判断比例系数k，然后再求其余自变量和因变量的值，灌输了“待定系数法”的数学思想.

3 理解数学——关注“怎样帮助学生学”

理解数学是教好数学的前提.教师“理解数学”的目的是让学生“理解数学”，这也是教学的首要任务.让学生能“理解数学”主要通过课堂教学来完成，而进行课堂教学的效果要依托于教学设计.从课堂本身出发，教师更应重视教学设计，使教学设计的落脚点放在“怎样帮助学生学”，关注:学生学习这一知识点的起点是什么？难点在哪里？怎样突破难点？怎样把复杂的问题通过层次设计使学生比较容易理解，理解深刻?

案例3 二元一次方程组解法1(案例来源:浙江省金华市三区教研活动公开课).

(1)

(2)

学生尝试解答后,教师请学生口答解题过程.

生1：把式(2)代入式(1)得y=3，代入式(2)得x=1.

师：你们和他的答案一样吗？

生(全体)：一样！

师：为什么把式(2)代入式(1)呀？为什么把y=3代入式(2)而不代入式(1)？

生2：这样可以直接求出x，更简单.

师：怎样检验？

生3：代入方程组中的每一个方程,看方程2边是否相等.

师：例1的解题步骤是什么？先做什么？再做什么？

生4：代入消元→回代求解→检验作答.

师：还有哪些注意点？

生5：整体代入时要添加括号、最后要检验.

本节课的核心思想是消元与转化，除此之外，还涉及到程序化思想和简化、优化思想，在教学中也应注意适度渗透.同时教师还应时刻在课堂中把基本的数学思想方法与知识、技能融于一体，使学生在学习知识、技能的同时领悟到一定的数学思想方法，在运用思想方法的同时巩固知识、技能，这样，思想方法就有了载体，知识技能就有了灵魂，真正做到“学为中心”的课堂.鉴于以上认识，笔者对本环节进行了如下改进：

讲解例题后，变式练习：

(1)如何把方程组转化为一元一次方程？怎样转化比较简便？

(2)哪个未知数的值可以先求出来？从哪里入手？问题解完了吗？

(3)另一个未知数的值如何求？

(4)可以把x=y-2代回x-y=-2求解吗？为什么？

(5)先求出的一个未知数的值可以代回到方程组中，求出另一个未知数的值吗？代入哪个更简单？

(6)你能总结代入法解二元一次方程组的一般步骤吗？

代入消元法解二元一次方程组的基本步骤如图1所示：

图1

程序化解法也有消极的一面,它使运算成为一种机械操作.可能出现的情况是：学生遇到特定的情景，就机械地套用代入法的一般步骤；面对三元一次方程组时更是感到束手无策.

对问题的设置改进如下：

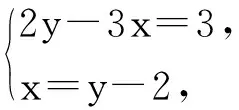
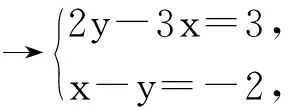
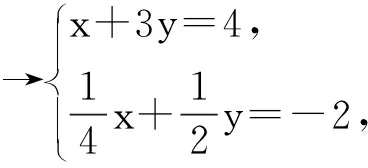
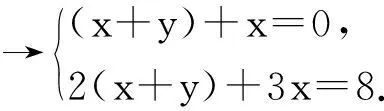
解二元一次方程组的本质是消元，即把“二元”转化为一元.消元的基本方法是代入法、加减法，这2种方法的本质差别在消元的具体步骤上.代入消元先要将其中一个二元一次方程变形成用一个未知数的代数式表示另一个未知数的形式.变形的基础是等式的基本性质，这一步变形也是学习一次函数内容必备的基础，因此这种变形能力对学生后续的学习非常重要.加减消元法的本质内涵是整体思想，学生先利用等式的性质把2个方程中其中一个未知数的系数变成相同，这样整体加减时，才能达到消元的目的.加减消元中的整体思想是数学中常用的思想方法.从2种解法的运算程序和推理步骤看，代入消元法更具通性，加减消元法侧重于方程变形的技巧，因此教材安排2个课时让学生先学习代入法，再学习加减法.通过这样的设计改进，帮助学生理解解二元一次方程组的通性通法，真正打造“学为中心”的成长课堂.

每个学生的学习品质存在差异，对数学的理解存在差异，而教材的重、难点是教学的重心所在，是学生认知矛盾的焦点，也是学生学习的困惑点.学习是新知识的生长过程，学生在学习的过程中往往会遇到思维的障碍.“学为中心”的成长课堂要求学生在阅读课本中的概念、定理等文本内容以后，帮助学生深入理解概念的内涵或定理的条件、结论而设置问题，面对不同层次的学生，使不同的学生思有所得、思有所悟.立足于学生“最近发展区”的问题串设计给学生搭建起“适切”的“脚手架”，由浅入深，环环相扣，层次递进，形成了一条完整的问题链，满足了不同层次的学生需求，帮助学生思考问题、分析问题，突破了学困点.

从教为中心到学为中心，是从研究怎样教，到研究怎样学，即怎样引导学生学、怎样帮助学生学的过程；是让学生尝试自主学习，主动获取知识的过程；是生生合作、小组交流的进一步升华.“学为中心”的成长课堂，要求教师变“规定描述”为“引导建构”，教学设计要找准知识的生长点，重学生感悟；变“列举告知”为“辨析发现”;要能拓展知识的“延伸点”，重教师引悟；变“真题训练”为“内化匹配”;要能突破学生的学困点，重学生顿悟.

[1] 李海东.理解数学是教好数学的前提——“中学数学核心概念、思想方法结构体系及其教学设计的理论与实践”初中第五次课题会议成果综述[J].中学数学教育，2010(4)：1-4.

[2] 向慧英，李家宝.联系实际巧设计 生成新知见实效——反比例函数的定义的教学实录及评析[J].中学数学教育，2011(12):22-26.[3] 徐晓红.问题设计应基于理解[J].中学数学教学参考：中旬，2012(1/2):25-27.

[4] 杨红芳.殊途能否同归——两节同课异构案例引发的思考[J].中小学数学：初中版，2011(11)：33-35.