例谈局部调整法在不等式证明中的应用

●张小明

(海宁市高级中学 浙江海宁 314400)

在中学数学竞赛中，局部调整法(又称磨光法)是证明不等式常用的手段与技巧.理论上其逐步逼近目标，直至最后彻底解决问题，实际上它主要可以表示成如下定理1～4.本文选用一些常见的数学竞赛题和网络流行题为例，说明局部调整法的作用.

定理1 设n∈N,n≥2,I⊆(-∞,+∞)是一区间，若对于任意的x1,x2,…,xn∈I，n元连续对称函数f满足

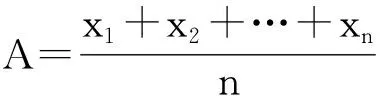
定理2 设n∈N,n≥2,I⊆(0,+∞)是一区间，若对于任意的x1,x2,…,xn∈I，n元连续对称函数f满足

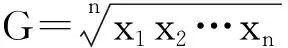
一般称定理1为“和调整”(可参考文献[1])，定理2为“积调整”.

1 任意2个自变量之间的调整

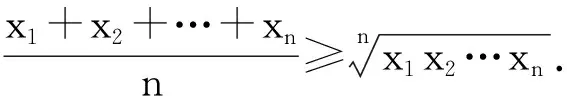
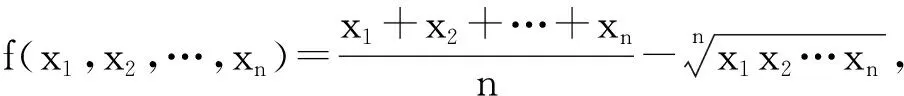
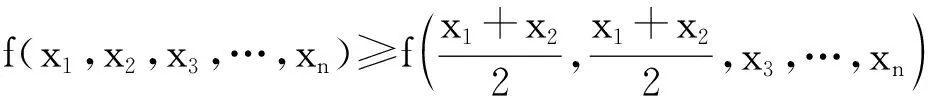
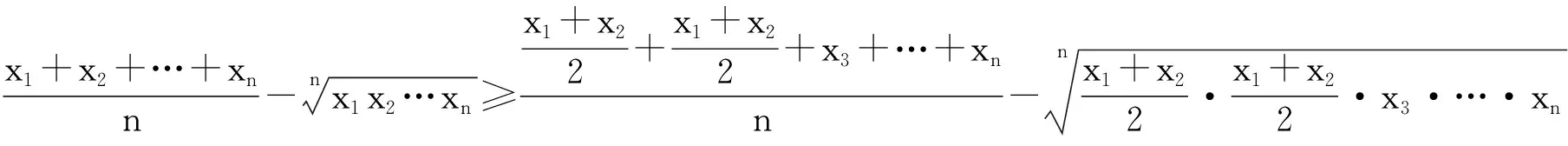
由定理1,知f(x1,x2,…,xn)≥f(A,A,…,A)，即

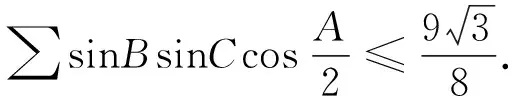
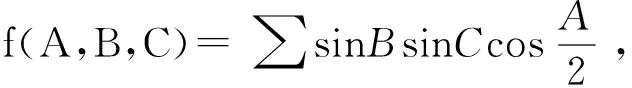
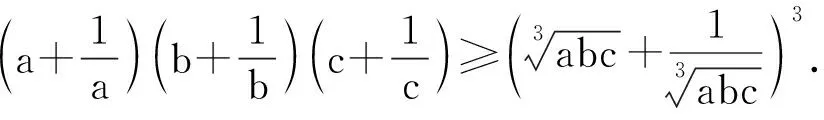
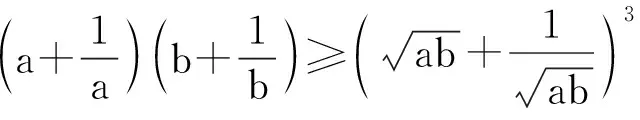
2 2个特定自变量之间的调整

2.1 在最大值与最小值之间的调整

定理3 设n∈N,n≥2,I⊆(-∞,+∞)是一区间，若对于任意的x1,x2,…,xn∈I，当x1≥x2≥…≥xn-1≥xn时，n元连续对称函数f满足

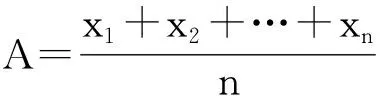
定理4 设n∈N,n≥2,I⊆(0,+∞)是一区间，x1,x2,…,xn∈I，当x1≥x2≥…≥xn-1≥xn时，n元连续对称函数f满足

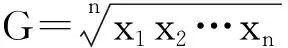
例4 设a1,a2，…，an均为正数,a1a2…an=1，求证：

证明 由对称性不妨设a1≥a2≥…≥an，且设

由定理3,知f(a1,a2,…,an)≥f(1,1,…,1)=0,即证.

与例4和练习题2相关的结果可参见文献[2].

2.2 自变量最小(大)值不参与的调整

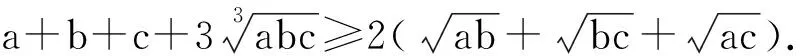
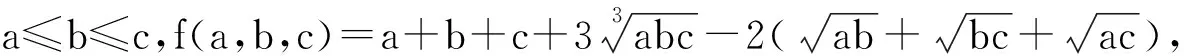
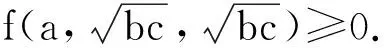
例6 设x≥0,y≥0,z≥0,t≥0，x+y+z+t=4,求证：

(1+3x)(1+3y)(1+3z)(1+3t)≤130+126xyzt.

证明 不妨设x≥z≥y≥t，f(x,y,z,t)=130+126xyzt-(1+3x)(1+3y)(1+3z)(1+3t).此时z+t≤2,zt≤1，从而

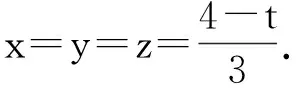
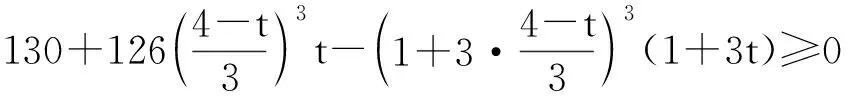
例6的证法已经把本文介绍的技巧集于一身，它是自变量最小值t不参与调整的情形下，自变量的最大值与次小值进行“和调整”，从而由定理3知：除t外，其实自变量都能调整到相等，不妨设为s，最后证明二元函数f(s,s,…,s,t)≥0.

3 其他情形的局部调整法

例7 已知a≥0,b≥0,c≥0，a+b+c=1，求证：(1-a2)2+(1-b2)2+(1-c2)2≥2.

证明 设f(a,b,c)=(1-a2)2+(1-b2)2+(1-c2)2.先证f(a,b,c)≥f(0,a+b,c)，其等价于

(1-a2)2+(1-b2)2+(1-c2)2≥(1-0)2+[1-(a+b)2]2+(1-c2)2,

由1=(a+b+c)2≥(a+b)2=a2+2ab+b2知上式为真.此时f(a,b,c)≥f(0,a+b,c)=f(c,a+b,0)≥f(0,a+b+c,0)=2,即证.

例8 已知正实数x1,x2,…,xn，满足x1x2…xn=1，求证：

(1999年罗马尼亚数学奥林匹克国家队试题)

证明 先证如下的结论(1)和结论(2)，此处略.

(1)若x≥n-1，y≥n-1，则

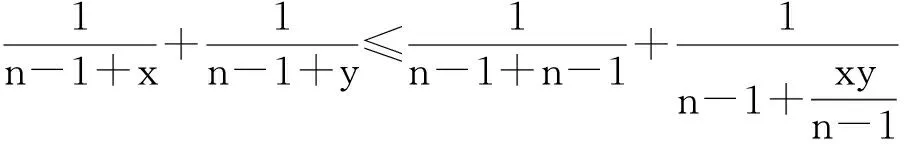
(2)若x≤n-1，y≤n-1,则

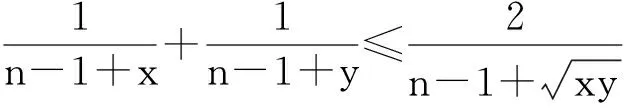
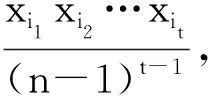
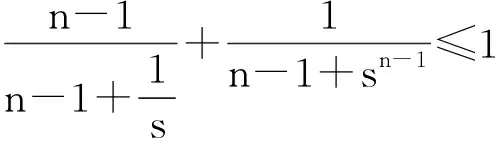
由于易证最后一式的左边关于s单调且能在s=1时等号成立，即证.

关于局部调整法，还有微分判别准则，具体可见文献[3].

4 练习题

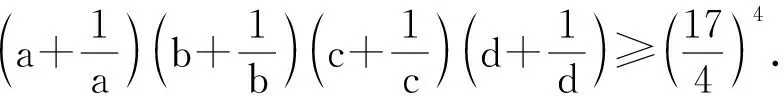
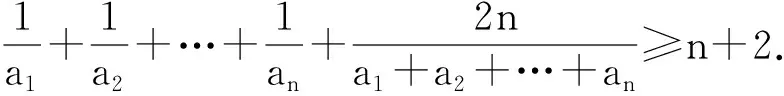
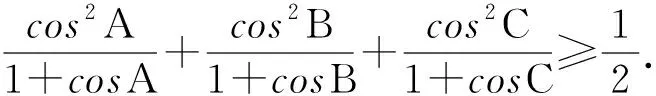
(2005年全国高中数学联赛试题)

(在成文过程中，得到“局部调整法”研究专家石世昌先生的帮助，在此表示衷心感谢！)

[1] 赵德钧.关于求多元对称函数极值的一个磨光法[J].数学通报,1998(12)：31-32.

[2] 杨学枝.数学奥林匹克不等式研究[M].哈尔滨:哈尔滨工业大学出版社,2009：330-331.

[3] 张小明，褚玉明.解析不等式新论[M].哈尔滨:哈尔滨工业大学出版社,2009:217-259.